Games and Mathematics (10 page)

Mathematics started as simple models of the real world – counting objects and measuring – but even the most abstract mathematics often turns out to model some part of reality, a mystery which no one has solved and to which we shall return when we look at mathematics in science.

When the ancient Greeks studied the conic sections they had no idea that Kepler, Galileo
and Newton would use them to explain the motions of the planets and falling bodies: the Greeks thought the planets moved in simple circles! When mathematicians obtained the square roots of negative numbers while solving quadratic and cubic equations, they were mystified – they did not know they would eventually be used by electrical engineers, among many other uses.

Chess and Go have entirely lost touch with the real world conflicts they model but mathematics has never lost touch with reality without which it would be incomparably less rich, and would perhaps have stagnated totally – just one of the many differences between mathematics and abstract games.

Recreations tend to emphasise the synthetic construction of solutions, and proofs that show that constructions are adequate – for example, by displaying a set of pentominoes
filling a certain shape – while deeper questions often seem impossible to answer. For example, what formula will predict the number of arrangements of the 12 pentominoes which will fill a rectangle 5
m
by
n
?

It is hard enough to calculate the answer for particular rectangles by brute force using a computer program: a formula for the number seems hopelessly out of reach, not least because the shapes of the pentominoes are so ‘irregular’. Pentominoes fit more or less awkwardly into corners or against edges, some
pentominoes fit each other like a key in a lock but others don't, and there is just
so little pattern
in them.

We cannot say that the 12 pentominoes are totally arbitrary because they are, after all, forced by the condition that each consists of 5 identical squares joined along complete edges – but their combinations do seem pretty arbitrary and not amenable to elegant calculation or simplification.

In this respect many mathematical recreations are as close to abstract games as to mathematics. Just as the rules of chess show a degree of arbitrariness that usually precludes us from
proving
our conclusions other than by analysing a tree of possibilities, so some mathematical objects – pentominoes are an example – seem so arbitrary that we may wonder whether we shall ever understand them deeply enough to replace trial-and-error methods by much shorter proofs.

We saw that the game of Nine Men's Morris has been completely solved but only by using a computer to check possibilities, not by using deep insights into the structure of the game to create a short proof. No doubt the programmer used as many short cuts as possible, but he could not do more because – as far as we know – the game simply does not possess any deep mathematical structure. The rules of the game, the movements of the pieces, and the size of the board (in all their different variations) are too arbitrary and too little patterned to force deep structure. The shape of the board is also somewhat arbitrary like the boundaries of many boardgames that give peculiar roles to corner and edge squares (an especially significant feature of Go).

This is one reason why these game are so fascinating: their structures can be understood scientifically through experience but they can never be reduced to mathematical proofs, so the possibilities for subtle insights and deep intuition are endless and even the very strongest players play imperfectly.

It is true that certain special cases can be treated mathematically. As we saw, Elwin Berlekamp and David Wolfe have written
Mathematical Go: Chilling Gets the Last Point
on the endgame at Go, but the book is only possible because as the game proceeds the board (as we noted earlier) is naturally divided into mutually separate regions of still-active play which can be analysed by combinatorial game theory. Endgame success does not promise to spread to the opening and middle game.

Every property and feature of such abstract games is forced by the rules but there may be no means of reducing their complexity to the relatively simple patterns that mathematicians can handle, and even if you occasionally prove a
global proposition about a game, for example that Hex should be a win for the first player, most smaller-scale local propositions remain unprovable.

We can illustrate what we mean with the above question. How would we prove that 11 is prime? Well, 11 is odd so it is not divisible by 2 and 11 + 1 = 12 is a multiple of 3 and 11 – 1 = 10 which is a multiple of 5, and 11 < 14 which is 2 × 7. So 11 is prime.

It's obvious, is it not? Yes, indeed, but the fact is that we have only confirmed this
obvious
fact by
checking
the possibilities. Given that it is so obvious, the check is not especially short, but there is no simpler proof which would make checking unnecessary.

Pretty much the same is true if we wanted to check that 97 is prime. Suppose that we realise that all its prime factors are less than or equal to √97 which is under 10 so that we only need to check 2, 3, 5 and 7 as possible prime factors. The check is simple enough and much faster than testing all the primes up to 50, but it hardly qualifies as a snappy proof.

The same is true, however, of more powerful tools for checking the primality of far larger numbers. Each specific tool is too powerful to be efficient for small numbers: then a point is reached at which the tool is worth using, but eventually it gives out by becoming too slow for all practical purposes and a more complex and powerful tool is sought.

These thoughts suggest the question, ‘Are there coincidences in mathematics?’ For example, all number puzzle buffs know that 6 = 1 × 2 × 3 = 1 + 2 + 3, and that 153 = 1
³
+ 5
³
+ 3
³
, so it is one of those rare numbers that are the sum of the cubes of all their digits (in the decimal system). Is there anything deep about this fact, or is it, well, a random fact with no further significance?

G. H. Hardy definitely thought it the latter. When he wished in his book,
A Mathematician's Apology
, to give examples of mathematical theorems that were not ‘serious’ he suggested as one example this property of 153, shared by 370, 371 and 407 and no other numbers under 1000. Such facts, he suggested, were suitable for puzzle columns but he dismissed them as serious mathematics, not least because ‘the proofs…are not capable of any significant generalisation’ [Hardy
1941
/1969: 105].

In other words, they are isolated, unconnected, and unproductive – which suggests that perhaps they are indeed coincidental, like features that you spot in the landscape that certainly exist, but are unrelated to any other feature.

Let's make a rough distinction between
checking
and
fast-proving
. The distinction must be fuzzy because checking can often be speeded up by using little tricks – such as realising that any prime factor of
N
must be less than or equal to √
N
– without having a really quick proof, and many proofs are pretty slow.

When would you expect to have a fast-proof for a theorem and when might you have to be satisfied with a mere check? One answer is that if you are working in a miniature world with very strong patterns then you might expect to prove just about anything with no resort to checking. Euclidean geometry is a perfect example. The Euclidean plane has a very simple and powerful structure and so it is plausibly no coincidence that there are literally thousands of Euclidean theorems which are easy to prove – and prove in many different ways.

There is another reason which may explain why Euclidean theorems are easy: the questions asked! Euclidean geometry is about lengths and angles, areas and surfaces, parallels and perpendiculars, concurrent lines and collinear points, all of which are simply defined in Euclid's terms.

Elementary arithmetic is also very simple, but the theory of numbers soon leaves that simplicity behind when we ask questions about the prime numbers or the ‘arithmetical functions’. As we operate Erastosthenes’ sieve
, we only learn what the next prime is to be at the end of the previous sieving step. Each prime depends for its definition on the sequence of previous primes in a way that squares and cubes don't (see pages 197--8).

Suppose that we ‘crossbreed’ Euclidean geometry with prime numbers and start asking questions about quadrilaterals whose sides and diagonals are prime. What do we discover? Curiously, we don't know, because mathematicians never ask such questions. They do consider structural analogies between Euclidean geometry and numbers when they exploit coordinate geometry, but they don't suddenly jump in and add the qualification ‘it must be a prime number!’ to questions about quadrilaterals.

Most mathematicians would suspect that such questions would be instantly classifiable with Hardy's unserious 153 property, instinctively feeling that it will not lead anywhere interesting because the very ideas seem incompatible: the motivation of mathematics comes from finding deep and beautiful connections
but here these seem most unlikely to exist. The mathematician is put off by such questions because they appear to be
ugly
. Somehow, prime numbers and Euclidean geometry do not ‘mix’.

There is another way to create ‘strange’ questions, though these questions are actually asked very seriously and they are very interesting. Suppose we start with a number like π which can be represented in many ways as a series with a striking pattern. Here is one, due to Euler, for π
²
/6:
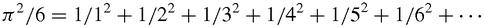Now we calculate the value of π as a decimal fraction:
The first series has an obvious pattern but the decimal which we have started to write out as a sum of powers of 1/10 looks to have no pattern at all. But why should it? No one knows of any connection between the number π and the base of the decimal system so the ‘cross’ between them is somehow unnatural and we might expect to get a ‘random’ result – which is exactly what mathematicians suspect: that the digits of π as a base 10 decimal are completely random because its representation is totally arbitrary. The computer scientist's motto is, ‘Garbage in, garbage out.’ We might say, ‘Pattern in, pattern out’ – and if you put in no pattern you get out randomness.

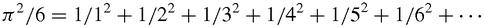
This is the very opposite of the result that Descartes got when he ‘crossed’ Euclidean geometry with a set of coordinates. The coordinates represented Euclid's basic features so well that all of Euclid's system appeared clearly and (usually) simply in Descartes's coordinate geometry – while the distinctive features of Descartes's coordinate perspective fed back into Euclidean geometry, rather as physical science has fed back into mathematics generally. Coordinates are a brilliant
representation
of Euclidean geometry – whereas the decimal system of notation seems to be a very bad representation of the number π.

Let's return for a moment to our starting point, mathematical recreations, and imagine a sequence of more-and-more game-like recreations. At the
mathematical pole the game-element is small and we expect to fast-prove everything: at the game-like pole, everything is arbitrary and we expect to do no better than check our conclusions. What will happen in between? There will be a boundary – fuzzy, no doubt – around which problems will be either just capable, or just incapable, of a more-or-less fast-proof. Where is that boundary? That's difficult to say. It could be that some problems regarded today as ‘obviously’ mathematical are in fact sufficiently arbitrary to be unmanageable and unsolvable.

A plausible candidate is the problem of the normality of numbers such as π or e. As decimals, they appear to be completely random, or
normal
, meaning that every digit 0 to 9 occurs 1/10 of the time, every pair such as 45 occurs 1/100 of the time, and so on. Yasumasa Kanada has calculated 1241100000000 digits of π and checked a trillion for the frequencies of the digits 0 to 9. The frequencies are not abnormal for a random sequence. [
www.super-computing.org/pi_current.html
]

However, even if normality turns out to be provable, there will no doubt be more arbitrary situations which will not be. If such situations are finite then proof by checking will be at least a theoretical possibility even if the computation involved is too vast to be practicable, but if the situation is unbounded then no fast-proof may be available and checking will also be impossible, in which case propositions which are forced by the rules may be impossible to establish.

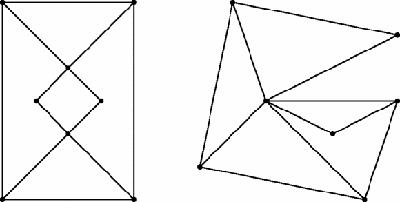
Graph theory is another candidate for extreme arbitrariness. Graphs can be highly patterned, like the graph on the left in
Figure 5.1
, in which case many precise conclusions can be proved about them, but the
typical
graph is more like that on the right, highly arbitrary and unpatterned.

Conclusions about graphs can typically be checked ‘by hand’ if the graph is small enough – but most graphs aren't – or they can be fast-proved to lie within
certain limits by global arguments which do not give precise answers, unless the graph is very small. What we cannot do, apparently, is fast-prove precise results. Since the nodes and the edges of a graph can be chosen ‘at random’ that conclusion is hardly surprising.

We can therefore conclude that there are limitations on the strength of mathematics due to the very
game-likeness
of mathematics, which often involves a degree of arbitrariness, suggesting a limiting boundary. Mathematics depends on pattern and structure – and their correlate, beauty – to make mathematics manageable, and beyond some uncertain limit, when it becomes too game-like, it will be unmanageable and proof will vanish away.