Games and Mathematics (32 page)
Read Games and Mathematics Online
Authors: David Wells
Alternatively,
you don't need to draw a picture at all, you just lay out some pebbles or counters. By summing these sequences we are doing nothing to help the handyman, surveyor, businessman or housewife. We are simply stepping back and noticing that the odd numbers are
interesting
. ‘Looking’, as we have already said, doesn't have to mean looking at a diagram. We can ‘look’ at algebraic equations, formulae, or pages of manipulation and ‘see’ what is going on, and ‘see’ possibilities.
you don't need to draw a picture at all, you just lay out some pebbles or counters. By summing these sequences we are doing nothing to help the handyman, surveyor, businessman or housewife. We are simply stepping back and noticing that the odd numbers are
interesting
. ‘Looking’, as we have already said, doesn't have to mean looking at a diagram. We can ‘look’ at algebraic equations, formulae, or pages of manipulation and ‘see’ what is going on, and ‘see’ possibilities.
Linguists have noted that the commonest use of ‘I see what you mean’ is to mean, ‘I understand you.’ We study a position at chess or a mathematical diagram of equation to ‘see what it means’.
One of the most famous anecdotes in the history of mathematics tells of the young Gauss in first school. Told to add up the numbers from 1 to 100, the rest of the class worked away at their slates while Gauss wrote down the answer, 5050.
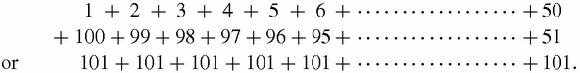 So the grand total is 101×50 = 5050. But this also equals 1/2×100×101 matching our previous general rule. Gauss ‘saw’ arithmetically or even algebraically, in this case, rather than geometrically.
So the grand total is 101×50 = 5050. But this also equals 1/2×100×101 matching our previous general rule. Gauss ‘saw’ arithmetically or even algebraically, in this case, rather than geometrically.
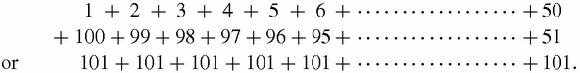
The Greeks were as intrigued by number patterns as they were by geometry though they made less progress in understanding them, partly because they had no algebraic notation and partly because they didn't ask the questions that would have
forced
them to make progress. As Nichomachus
(c.100 CE) explained in his
Arithmetic
, the numbers in this sequence,
are called triangular because, ‘their regular formations, when expressed graphically (Figure
16.11
), will be at once triangular and equilateral’.
forced
them to make progress. As Nichomachus
(c.100 CE) explained in his
Arithmetic
, the numbers in this sequence,
1 | 3 | 6 | 10 | 15 | 21 | 28‘and so on' |
16.11
), will be at once triangular and equilateral’.
Figure 16.11
A triangle of dots
A triangle of dots
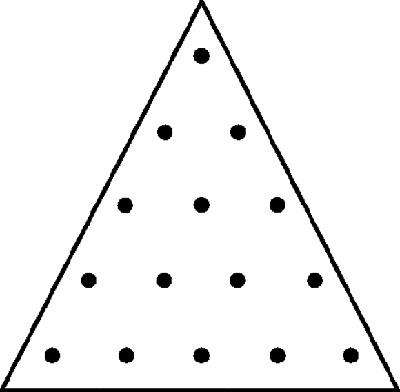
Figure 16.12
A square of dots
A square of dots

He then introduced the square numbers (Figure
16.12
), and the pentagonal numbers
, 1, 5, 12, 22, 35, 51, 70…. followed by the hexagonal, heptagonal and so forth, explaining that, ‘the doctrine of these numbers is to the highest degree in accord with their geometrical representation’ which he illustrated by pointing out that each square is divided diagonally into two triangles and every square number into two consecutive triangular numbers (as shown in Figure
16.13
) and that any triangular number added to the ‘next’ square number makes a pentagonal number (Figure
16.14
),
16.12
), and the pentagonal numbers
, 1, 5, 12, 22, 35, 51, 70…. followed by the hexagonal, heptagonal and so forth, explaining that, ‘the doctrine of these numbers is to the highest degree in accord with their geometrical representation’ which he illustrated by pointing out that each square is divided diagonally into two triangles and every square number into two consecutive triangular numbers (as shown in Figure
16.13
) and that any triangular number added to the ‘next’ square number makes a pentagonal number (Figure
16.14
),
triangles | 1 | 3 | 6 | 10 | 15 | 21 | 28 | … |
squares | 1 | 4 | 9 | 16 | 25 | 36 | 49 | … |
pentagonals | 1 | 5 | 12 | 22 | 35 | 51 | 70 | … |
Figure 16.13
Square of dots, divided into two triangles
Square of dots, divided into two triangles
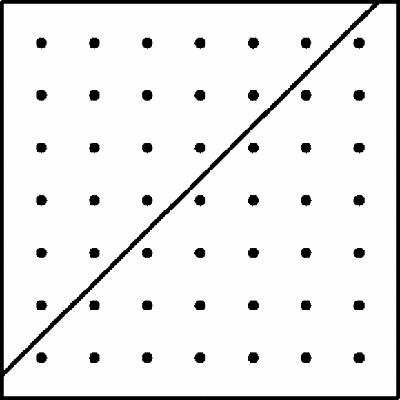
Figure 16.14
Pentagonal array of dots
Pentagonal array of dots
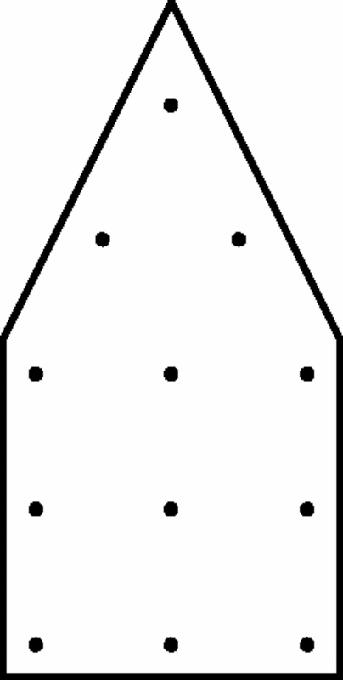
Figure 16.15
Hexagon divided into six triangles
Hexagon divided into six triangles
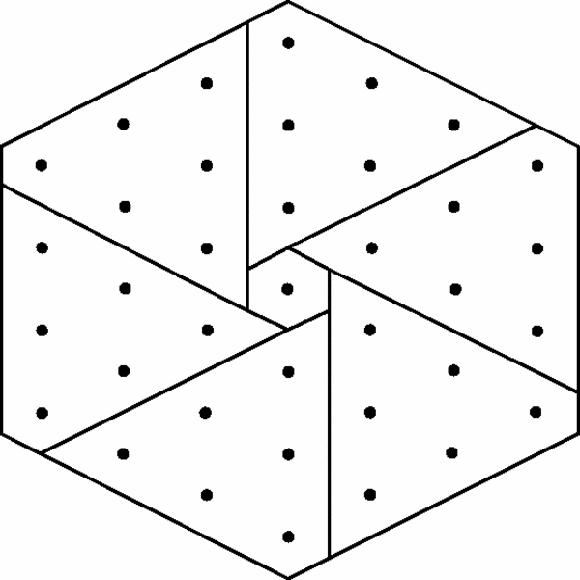
Every hexagonal number is the sum of six identical triangular numbers, plus 1:
H
n
= 6
T
n
−1
+ 1. The visual diagram allows any number of such identities to be ‘read off’ from this and similar figures, and ‘proved’ by sight, which would take relatively complex manipulation to prove by algebra – and algebra does not allow them to be ‘read off’ in the first place.
H
n
= 6
T
n
−1
+ 1. The visual diagram allows any number of such identities to be ‘read off’ from this and similar figures, and ‘proved’ by sight, which would take relatively complex manipulation to prove by algebra – and algebra does not allow them to be ‘read off’ in the first place.
The conclusions that Nichomachus
drew from dissecting the polygonal numbers
are simple examples of combinatorics or
The Art of Advanced Counting
[Berge
1971
]. His trick – compare Liu Hui – was to count the same set of objects in two ways, and compare the results.
drew from dissecting the polygonal numbers
are simple examples of combinatorics or
The Art of Advanced Counting
[Berge
1971
]. His trick – compare Liu Hui – was to count the same set of objects in two ways, and compare the results.
Partitions
is another topic where this trick works very well – up to a point. The partitions of a number are simply the ways of breaking it up into parts, including the original number as the first part. Here are the partitions of the integers 1 to 4:
 And following are the partitions of 8:
And following are the partitions of 8:

Unless we have missed a line, the number of partitions of 8, called p(8), is 22. The sequence of numbers of partitions starts like this:
Finding a formula for p(
n
) is extremely difficult but we can, by merely looking, draw some very powerful conclusions about special types of partitions. Figure
16.16
is a picture of one partition of 26.
is another topic where this trick works very well – up to a point. The partitions of a number are simply the ways of breaking it up into parts, including the original number as the first part. Here are the partitions of the integers 1 to 4:

n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
p( n ) | 1 | 2 | 3 | 5 | 7 | 11 | 15 | 22 | 30 | 42 | … |
n
) is extremely difficult but we can, by merely looking, draw some very powerful conclusions about special types of partitions. Figure
16.16
is a picture of one partition of 26.
Figure 16.16
Partitions diagram and the same, rotated
Partitions diagram and the same, rotated

If we read off the horizontal rows, then this is 26 = 8 + 6 + 6 + 5 + 1. However, if we rotate the diagram through ninety degrees, then we get the second diagram which shows the ‘dual’ partition: 26 = 5 + 4 + 4 + 4 + 4 + 3 + 1 + 1.
The largest number, 8, in the first partition is
the number of numbers
in the second partition, and the largest number in the second, 5, is the number of numbers in the first partition. This observation allows us to draw a remarkable conclusion:
the number of numbers
in the second partition, and the largest number in the second, 5, is the number of numbers in the first partition. This observation allows us to draw a remarkable conclusion:
The number of partitions of
N
with at most
M
parts equals the number of partitions of
N
in which no part exceeds
M
.
For example, these are the partitions of 5 into at most 3 parts, and into parts no greater than 3:

Why do these two partitions
match up so perfectly? The partition diagrams in Figure
16.17
show why. Notice that the fourth line above is symmetrical and the third and fifth lines match ‘in reverse’, so we have only drawn three diagrams.

match up so perfectly? The partition diagrams in Figure
16.17
show why. Notice that the fourth line above is symmetrical and the third and fifth lines match ‘in reverse’, so we have only drawn three diagrams.
Figure 16.17
Partitions diagram in three parts
Partitions diagram in three parts
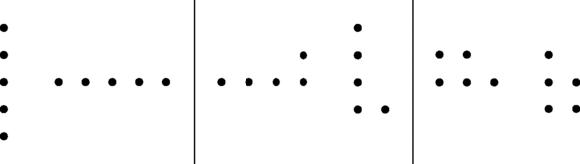
This conclusion is remarkable for two reasons. It is extremely simple and convincing and yet we need have no idea how many partitions there are of 5 with at most 3 parts. We ignore the very difficult problem of actually counting partitions and instead simply match them up, one-to-one. Now that really is Advanced Counting!
We can be confident of all these conclusions because we are dealing with very simple objects and sets of objects. Our conclusions really do seem both obvious and self-evident. According to the philosopher and mathematician Bertrand Russell,
self-evidence is a psychological property and is therefore subjective and variable. It is essential to knowledge, since all knowledge must be either self-evident or deduced from self-evident knowledge.
A few lines later he added, ‘self-evidence has degrees’ [Russell
1913
: 492]. That's true, and here it is of the highest degree. As the proverb says, ‘Seeing is believing’. We might add that this psychological quality of being self-evident is especially prominent in abstract games and other formal situations. Scientific theories, for all their power and extraordinary success, are never self-evident, and as for the
meaning
of poetry and painting, well, critics can and do argue endlessly.
1913
: 492]. That's true, and here it is of the highest degree. As the proverb says, ‘Seeing is believing’. We might add that this psychological quality of being self-evident is especially prominent in abstract games and other formal situations. Scientific theories, for all their power and extraordinary success, are never self-evident, and as for the
meaning
of poetry and painting, well, critics can and do argue endlessly.
Other books
Dave Barry's Homes and Other Black Holes by Dave Barry
Encyclopedia Brown and the Case of the Soccer Scheme by Donald J. Sobol
The Cowboy's Surrender by Anne Marie Novark
Julia's Child (9781101559741) by Pinneo, Sarah
Of Shadows and Dragons by B. V. Larson
Patchwork Dreams by Laura Hilton
The Faculty Club: A Novel by Danny Tobey
M&L03 - SS by Stacie Simpson
Fallen Ever After by A. C. James
Then Came You (The Wilde Sisters #2) by Marianne Rice