Games and Mathematics (27 page)
Read Games and Mathematics Online
Authors: David Wells
Quadrature: finding the areas under curves
The cycloid
What is the simplest way to calculate the area under a simple curve such as
y
=
x
3
, from, let's say, 0 to 10, from first principles?
y
=
x
3
, from, let's say, 0 to 10, from first principles?
The simplest and most obvious first move – which was used by Cavalieri (1598–1647) in his book,
Geometria Indivisibilibus
and Wallis (1616–1703) – would seem to be to divide the
x
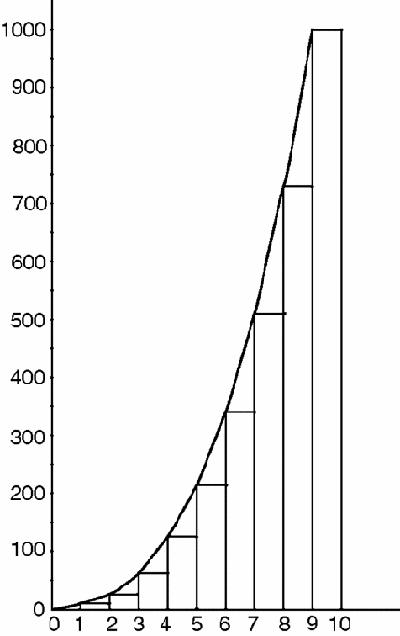
-axis from 0 to 10 into a number of equal parts, construct the vertical strips, as in
Figure 14.2
a, and then calculate the total area of all the strips.
Geometria Indivisibilibus
and Wallis (1616–1703) – would seem to be to divide the
x
-axis from 0 to 10 into a number of equal parts, construct the vertical strips, as in
Figure 14.2
a, and then calculate the total area of all the strips.
Figure 14.2a
y
=
x
3
divided into strips (underestimate)
y
=
x
3
divided into strips (underestimate)

With 10 equal parts, the sum of the areas of the strips underneath the curve is,
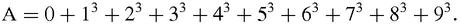
Adding these consecutive cubes is not hard, whether by hand, with a calculator or by using the formula that we have met before:
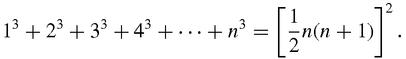 Whichever way, A = 2025. This, however, is a significant underestimate, so another smart tactic would be to repeat the sum as in
Whichever way, A = 2025. This, however, is a significant underestimate, so another smart tactic would be to repeat the sum as in
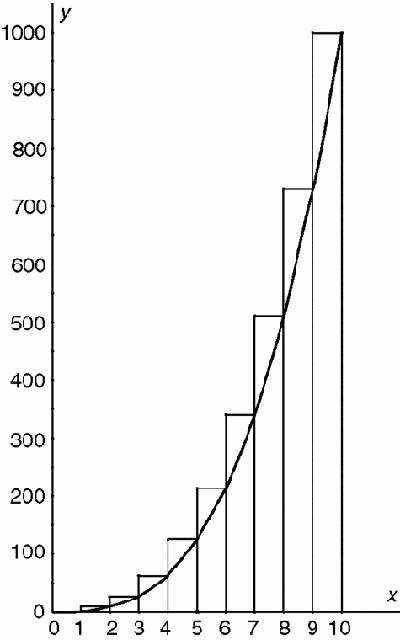
Figure 14.2b
, to get an overestimate:
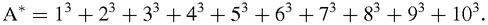
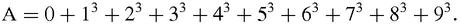
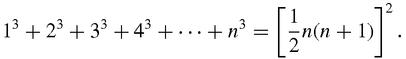
Figure 14.2b
, to get an overestimate:
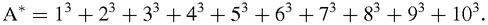
Figure 14.2b
y
=
x
3
divided into strips (overestimate)
y
=
x
3
divided into strips (overestimate)

A* = 3025; so we expect the average
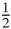 (A + A*) to be a much better approximation, and indeed it equals 2525 whereas the actual area is, by elementary calculus, 10000/4 = 2500. The error is exactly 1% which seems quite good for such a basic and unsophisticated strategy which can be made much more accurate by dividing the area into many more strips.
(A + A*) to be a much better approximation, and indeed it equals 2525 whereas the actual area is, by elementary calculus, 10000/4 = 2500. The error is exactly 1% which seems quite good for such a basic and unsophisticated strategy which can be made much more accurate by dividing the area into many more strips.
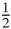 (A + A*) to be a much better approximation, and indeed it equals 2525 whereas the actual area is, by elementary calculus, 10000/4 = 2500. The error is exactly 1% which seems quite good for such a basic and unsophisticated strategy which can be made much more accurate by dividing the area into many more strips.
(A + A*) to be a much better approximation, and indeed it equals 2525 whereas the actual area is, by elementary calculus, 10000/4 = 2500. The error is exactly 1% which seems quite good for such a basic and unsophisticated strategy which can be made much more accurate by dividing the area into many more strips.On the other hand, adding cubes is not that simple, and if we want to use the same strategy for finding the area under
y
=
x
4
or
y
=
x
5
then each time we raise the index we need a new formula for the sums of
n
th powers of
consecutive integers. This is certainly a general method but it is not a simple general method. Fermat had a better idea, a sharper strategy.
y
=
x
4
or
y
=
x
5
then each time we raise the index we need a new formula for the sums of
n
th powers of
consecutive integers. This is certainly a general method but it is not a simple general method. Fermat had a better idea, a sharper strategy.
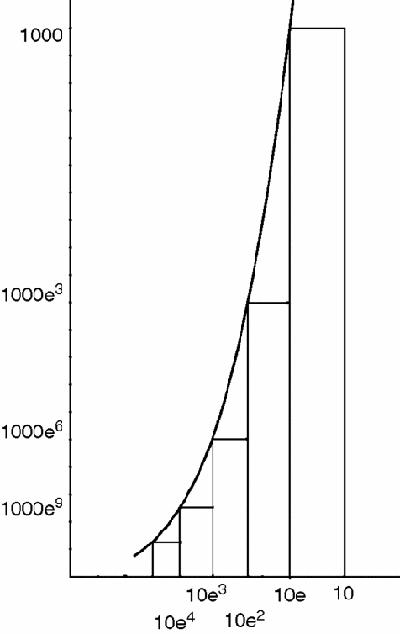
Using his method, you divide the
x
-axis from 0 to 10 not into equal parts, but into unequal parts by first marking the points 10, 10e, 10e
2
, 10e
3
, 10e
4
, 10e
5
, and so on, where e is chosen to be less than 1 (
Figure 14.3
). At first glance this is more complicated than the first method, but that is an illusion. Fermat, like a good chess player, has looked ahead and seen that this leads to a very
simple
calculation. The sum of the strips is now equal to, counting backwards from the right:
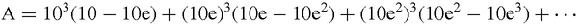
x
-axis from 0 to 10 not into equal parts, but into unequal parts by first marking the points 10, 10e, 10e
2
, 10e
3
, 10e
4
, 10e
5
, and so on, where e is chosen to be less than 1 (
Figure 14.3
). At first glance this is more complicated than the first method, but that is an illusion. Fermat, like a good chess player, has looked ahead and seen that this leads to a very
simple
calculation. The sum of the strips is now equal to, counting backwards from the right:
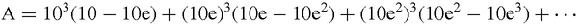
Figure 14.3
Fermat's unequal strips
Fermat's unequal strips

This is an infinite series which may already be a bonus. Infinite series are often easier to add up than their partial sums. In this case the sum is equal to,
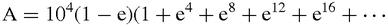
and the sum of this simple geometric series – so much easier to sum than the consecutive cubes – is,
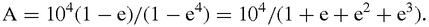 In order to make the approximate sum more accurate we let e tend to 1, and the area then tends to 10
In order to make the approximate sum more accurate we let e tend to 1, and the area then tends to 10
4
/4, as before [Boyer
1945
]. Unlike the original method, however, Fermat's cunning strategy can be easily used for any integral power of
x
.
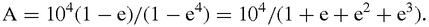
4
/4, as before [Boyer
1945
]. Unlike the original method, however, Fermat's cunning strategy can be easily used for any integral power of
x
.
The cycloid is generated by a point moving on the circumference of a circle rolling along a straight line. The circle on the left of
Figure 14.4
starts with a vertical diameter PT. After rotating through 180° the same diameter becomes TP, and after completing a circle of 360° it returns to its initial orientation PT. Meanwhile the point P has traced one complete arc of the cycloid, PPP.
Figure 14.4
starts with a vertical diameter PT. After rotating through 180° the same diameter becomes TP, and after completing a circle of 360° it returns to its initial orientation PT. Meanwhile the point P has traced one complete arc of the cycloid, PPP.
Other books
Animal Attraction by Tracy St. John
A Quiet Revolution by Leila Ahmed
Primal Song by Danica Avet
Juked by M.E. Carter
Working for Him by Willa Edwards
Hideaway Hospital Murders by Robert Burton Robinson
The Killing Song: The Dragon Below Book III by Don Bassingthwaite
Starfire by Kate Douglas
Waiting for Always by Ava Claire
Glory by Ana Jolene