Games and Mathematics (22 page)
Read Games and Mathematics Online
Authors: David Wells
The Seven-Circle Theorem
, and other New Theorems

, and other New Theorems
As if to illustrate that the variety of geometrical theorems is indeed endless, a curious small book was published in 1974 with this title.
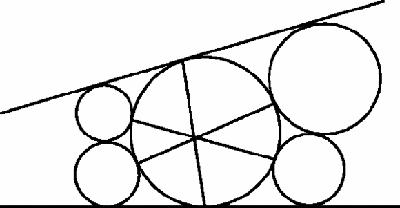
Figure 11.9
Seven-circle theorem
Seven-circle theorem

The elegant in Figure
11.9
is almost self-explanatory. A chain of six circles touches the inside of another circle. (They could also touch instead on the outside.) Join the points of tangency of ‘opposite’ circles in the chain and the three lines are concurrent. As always happens with such theorems, we can imagine one or more of the circles ‘blowing up’ until it becomes a straight line. In Figure
11.10
, two of the circles have done so, and all six circles are external.
11.9
is almost self-explanatory. A chain of six circles touches the inside of another circle. (They could also touch instead on the outside.) Join the points of tangency of ‘opposite’ circles in the chain and the three lines are concurrent. As always happens with such theorems, we can imagine one or more of the circles ‘blowing up’ until it becomes a straight line. In Figure
11.10
, two of the circles have done so, and all six circles are external.
Figure 11.10
Seven-circle theorem for two straight lines [Evelyn, Money-Coutts & Tyrrell
1974
: 32, 35, 39]
Seven-circle theorem for two straight lines [Evelyn, Money-Coutts & Tyrrell
1974
: 32, 35, 39]

As the title says, the book was also about ‘other new theorems’ including the heptagon theorem, the three-conics theorem and the
nine
-circle theorem.
nine
-circle theorem.
Where did these theorems come from? Did the three authors invent or discover them? Did they reason initially or start from experiment? We don't
know because they cunningly remark only that, ‘We derived a lot of enjoyment from evolving them’, adding that they have included rather a large number of diagrams ‘for their beauty of design, which we have found to have an appeal to many of our friends who are not mathematicians’ [Preface].
know because they cunningly remark only that, ‘We derived a lot of enjoyment from evolving them’, adding that they have included rather a large number of diagrams ‘for their beauty of design, which we have found to have an appeal to many of our friends who are not mathematicians’ [Preface].
It is a commonplace that modern science creates vast numbers of beautiful images, and mathematics-as-science is no exception. All the miniature worlds of mathematics are exceptionally beautiful, and elementary geometry is only unusual in making that fact so very obvious.
12
Numbers and sequences
Easy questions, easy answers
Numbers and sequences
Every teacher knows that pupils are far, far better at spotting number patterns than they are at proving them. Given the Fibonacci sequence:
in which each number is the sum of the previous two numbers, any pupil
with enough experience
to expect to find extra patterns might look at three consecutive entries, such as 3–5–8 or 5–8–13 and notice that:
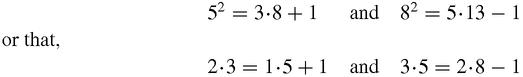 and so on. To work out why the differences are first +1 and then −1, and why the pattern (with this slight variation) always works, is far harder. To spot the pattern is rather easy
and so on. To work out why the differences are first +1 and then −1, and why the pattern (with this slight variation) always works, is far harder. To spot the pattern is rather easy
science
but to prove it is (relatively) difficult
mathematics
.
1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | … |
with enough experience
to expect to find extra patterns might look at three consecutive entries, such as 3–5–8 or 5–8–13 and notice that:
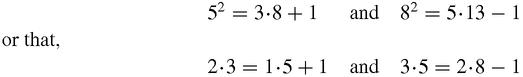
science
but to prove it is (relatively) difficult
mathematics
.
It is no surprise that the most brilliant mathematicians, such as Euler and Gauss, have been great pattern spotters.
The sums of squaresWe have seen that,
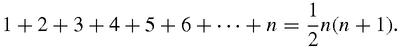 It is naturally tempting to wonder if you can add up the sequence of squares:
It is naturally tempting to wonder if you can add up the sequence of squares:
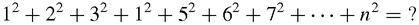 Yes, you can, and the standard result is
Yes, you can, and the standard result is
 n
n
(
n
+ 1)(2
n
+1) which always annoys me because the factor 2
n
+ 1 seems out of place. Anyway, let's try to find the
sum of the odd squares instead, which is less well known. A
scientific
approach is to calculate the first few sums and try to spot a pattern:
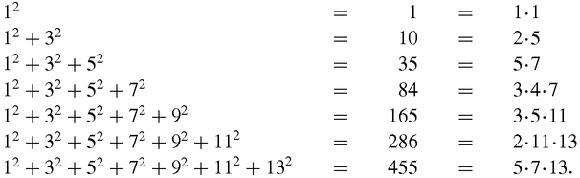 Since the sum of the squares is the product of three factors, with an extra factor of 1/6, we take this to be a giant hint and write down the factors of each number in the right-hand column. The last three rows are especially suggestive. The sums to 11
Since the sum of the squares is the product of three factors, with an extra factor of 1/6, we take this to be a giant hint and write down the factors of each number in the right-hand column. The last three rows are especially suggestive. The sums to 11
2
and 13
2
include the factors 11 and 13 but the sum to 9
2
does not include the factor 9. Where can it have gone to? Put on your Sherlock Holmes thinking cap or puff on your favourite pipe, and the answer will appear. All we have to do is to pinch the factor 1/6 from the sum of all the squares:
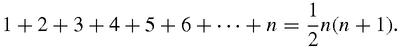
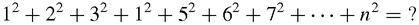
 n
n(
n
+ 1)(2
n
+1) which always annoys me because the factor 2
n
+ 1 seems out of place. Anyway, let's try to find the
sum of the odd squares instead, which is less well known. A
scientific
approach is to calculate the first few sums and try to spot a pattern:
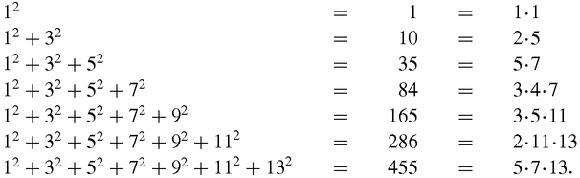
2
and 13
2
include the factors 11 and 13 but the sum to 9
2
does not include the factor 9. Where can it have gone to? Put on your Sherlock Holmes thinking cap or puff on your favourite pipe, and the answer will appear. All we have to do is to pinch the factor 1/6 from the sum of all the squares:
The sum of
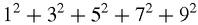 is
is
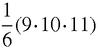 so the sum,
so the sum,
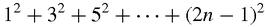 ought to be,
ought to be,
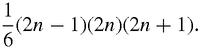 It is, though we haven't proved that conclusion. Before we leave this little experiment, we will make another observation: the factors 2 in 2
It is, though we haven't proved that conclusion. Before we leave this little experiment, we will make another observation: the factors 2 in 2
n
−1, 2
n
and 2
n
+ 1 suggest that we re-write the sum of the squares which is
 n
n
(
n
+ 1)(2
n
+ 1), as
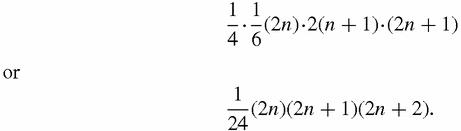 Aha! That annoying asymmetry has disappeared!
Aha! That annoying asymmetry has disappeared!
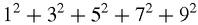
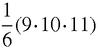
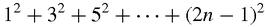
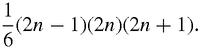
n
−1, 2
n
and 2
n
+ 1 suggest that we re-write the sum of the squares which is
 n
n(
n
+ 1)(2
n
+ 1), as
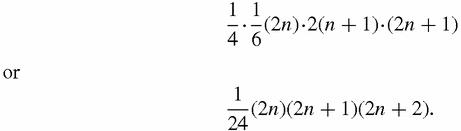
Many puzzles about the polygonal numbers are
relatively
easy to answer, plausibly because they show very strong patterns and, we might speculate, the stronger the pattern, the easier the proof. After all, proof depends on pattern, and it is by spotting patterns that ideas for proofs appear.
relatively
easy to answer, plausibly because they show very strong patterns and, we might speculate, the stronger the pattern, the easier the proof. After all, proof depends on pattern, and it is by spotting patterns that ideas for proofs appear.
There is a lot to be said for that large assumption, which we will meet again later. Here we are going to test it, by sketching some problems raised by the prime numbers
.
.
Other books
Better Dead by Max Allan Collins
The Scandal (Billionaire's Beach Book 4) by Christie Ridgway
Death to Pay by Derek Fee
Vampire Breath by R. L. Stine
Fortune's Son by Emery Lee
Chase Baker and the Seventh Seal (A Chase Baker Thriller Book 9) by Vincent Zandri
RBC05 - Bloodline by Elizabeth Loraine
The Silver Tower (The Age of Dawn Book 3) by Everet Martins
The Better Man (Chicago Sisters) by Amy Vastine
Bone to Be Wild by Carolyn Haines