Games and Mathematics (21 page)

Read Games and Mathematics Online

Authors: David Wells

Mathematics and geography
 
Mathematicians are explorers of many miniature mathematical worlds. Explorers often find the objects or phenomena that they discover novel and surprising and they do not always describe them accurately. Indeed, just because they are novel and surprising, early explorers may mis-describe them, misunderstand them, and give most misleading reports.
It is only after much further study that the ‘true nature’ of the kangaroo, or the manatee, or carnivorous plants are determined. The same is true of mathematicians exploring their miniature worlds. A perspective that naturally brings us to the subject of the mathematician as a scientist.
11
Mathematics as science
 
Introduction
 
The great Victorian scientist T. H. Huxley once made the mistake of claiming that mathematics was a deductive science modelled on Euclid in contrast to the natural sciences which were inductive, based on observation, experiment and conjecture. James Sylvester (1814–1897), an equally great mathematician, in a famous address to the British Association for the Advancement of Science in 1869, disagreed:
 
[Huxley] says ‘mathematical training is almost purely deductive. The mathematician starts with a few simple propositions, the proof of which is so obvious that they are called self-evident, and the rest of his work consists of subtle deductions from them’…we are told [by Huxley] that Mathematics is that study which knows nothing of observation, nothing of experiment, nothing of induction, nothing of causation.
 
Sylvester was appalled:
 
I think no statement could have been made more opposite to the undoubted facts of the case, that mathematical analysis is continually invoking the aid of new principles, new ideas and new methods, not capable of being defined by any form of words, but springing directly from the inherent powers and activity of the human mind, and from continually renewed introspection of that inner world of thought of which the phenomena are as varied and require as close attention to discern as those of the outer physical world…that it is unceasingly calling forth the faculties of observation and comparison, that one of its principal weapons is induction, that it has frequent recourse to experimental trial and verification, and that it affords boundless scope for the exercise of the highest efforts of imagination and invention.
 
Sylvester added that, ‘Induction and analogy are the special characteristics of modern mathematics’ [Midonik
1968
v.2: 370–1].
Whew! But Sylvester was right. Mathematicians, like game players, construct their own miniature worlds whose landscapes they explore in a scientific and game-like manner. In these new worlds are a wealth of objects, properties, and relationships which the mathematician observes and which – so often – appear to have a life of their own. We say that a series or sequence ‘goes on for ever’ or ‘tends to infinity’ or that a one shape is ‘transformed’ into another. We observe not merely static objects, lying as it were in museum cases, but dynamic scenarios which move and change. The fact that so many of these objects were constructed and named by mathematicians in the first place does not make them any less able to be studied by the methods of science: it just means that you hope to go one step further and mathematically prove your conclusions.
Empirical scientists can look, explore, conjecture and test, but not prove, so we might say that, yes, mathematics is also empirical but it is empirical-plus and it's
plus
because it is game-like, the crucial point.
The empirical but game-like nature of maths appears especially when we use physical drawings or models as aids to thinking. Archimedes
who was killed by a Roman soldier as he drew a geometrical diagram in the sand did not mistake the diagram for mathematical reality. It was a representation and a rather crude one, forced by the lack of cheap writing materials. A mere child could produce a more accurate representation today, with endless supplies of paper and accurate drawing instruments – and maybe a computer and a geometrical drawing package.
Such representations are essential because however well you can visualise it will at best be difficult and usually be impossible to do many experiments mentally. Computers have created new possibilities for calculation and representation and so given a boost to experimental and scientific mathematics – which, however, have always existed because mathematicians have always
explored
their
miniature worlds
.
 
Triangle geometry: the Euler line of a triangle
 
 
How were the theorems of triangle geometry
discovered? I can only conjecture that as with much of mathematics, it emerged from long hours of ‘playing around’.
[Davis
1995
: 206]
 
Euclidean geometry is a model of a physical plane so you can do your
experiments
on any flat plane surface. Rough experiments may do to begin with though of course you get more convincing results if your experiments are as accurate as possible.
The lines in actual geometrical figures are never infinitely thin; indeed, if drawn with a pencil or felt-tip pen they could even be a millimetre or more thick. Likewise, points can never be drawn to be infinitely small and dots are likely to be even wider than the lines (
Figure 11.1
).
Figure 11.1
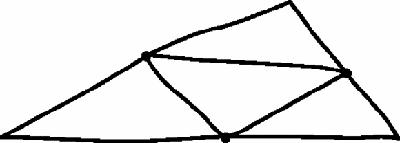
Hand-drawn triangle with mid-point triangle
 
 
This causes no confusion however, even to most school pupils who will not be muddled by a sketch like this in which the points are dots and the lines are visibly thick and not even straight. Because it's so easy to draw figures – and because it's fun to experiment! – it has been said that almost all of elementary geometry was originally discovered by experiment, and only later proved. Of course, if you are going to experiment then the diagram should be pretty accurate. Figure
11.2
is an example.
Figure 11.2
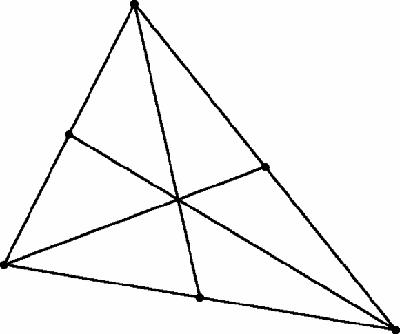
Triangle with mid-points and medians
 
 
We have drawn lines from each vertex of a triangle to the mid-points of the opposite sides. The lines
concur
, they pass through the same point which happens to be the centre of gravity of the triangle (usually called G): if this shape were cut out of cardboard then it would balance on a pin at this point.
This is only one of many centres of the triangle. Another centre can be found by drawing the perpendicular bisectors of the sides which concur at the centre of the
circumcircle
of the triangle, called the circumcentre (Figure
11.3
).
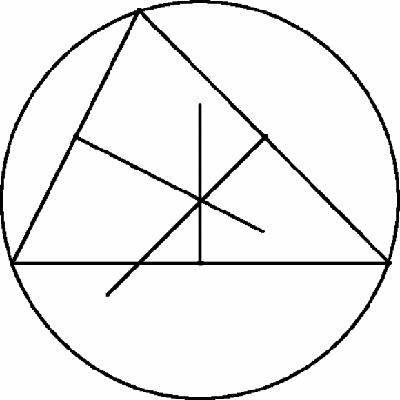
Figure 11.3
Triangle with circumcentre
 
 
The point where two perpendicular bisectors of two of the sides meet will be equidistant from all three vertices, and so it will lie on the third perpendicular
bisector also – and will be the centre of the unique circle through all three vertices.
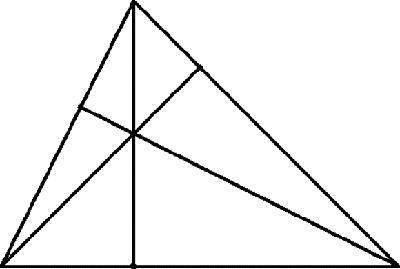
Figure 11.4
Triangle with altitudes
 
 
We could also draw the
altitudes
, the perpendicular lines from each vertex to the opposite side, which concur at the
orthocentre
(Figure
11.4
). What happens if we draw all three of these centres on the same diagram? We might suspect that we would get three unrelated points because, after all, what connection would you expect between three ‘centres’ constructed in such totally different ways?
Figure 11.5
Triangle with Euler line
 
 
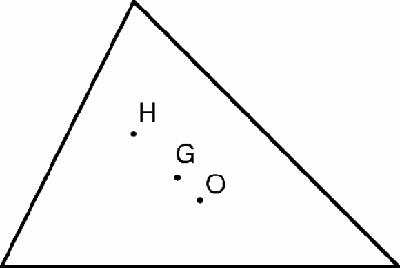
The answer is surprising. The orthocentre, H, the circumcentre, O, and the centre of gravity, G, lie on the same straight line (Figure
11.5
), called the Euler
line of the triangle after Euler who first discovered this fact. As it happens, the figure has an extra property, also noticed by Euler. Point G divides the line OH in the ratio 1 to 2.
Modern geometry of the triangle
 
The Greeks knew the four basic triangle points, the centre of gravity, the incentre, the circumcentre and the orthocentre. Subsequently, many more points have been discovered, described and analysed, many of them without a doubt by ‘playing around’ which is an aspect of creativity in every human endeavour, not just mathematics.
Euler and Feuerbach between them discovered the nine-point circle
(Figure
11.6
).
Figure 11.6
Triangle with nine-point circle
 
 
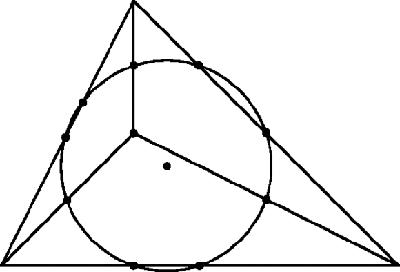
The nine points which always lie on a circle are the mid-points of the sides, the feet of the perpendiculars from each vertex to the opposite side, and the points half-way between each vertex and the orthocentre. I can't resist mentioning that when I was aged 12 or 13 we had to learn to prove this theorem, following Mr Straw's explanation on the blackboard. (However, we did not have to prove any of the other properties of the nine point circle, for example that it touches the incircle and the three excircles of the triangle.)
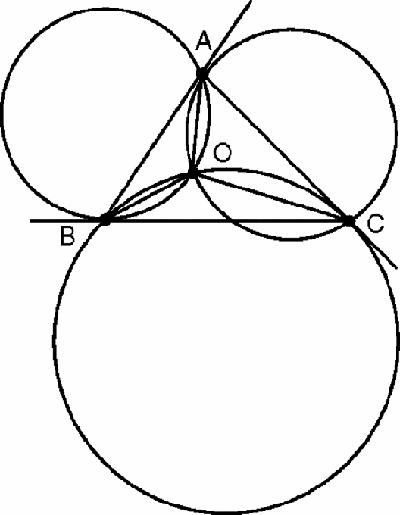
The nine-point circle was a great novelty to traditional Euclidean geometers and the start of a revival. In 1873 Emile Lemoine (1840–1912) read a paper to the French Association for the Advancement of Science on ‘Some properties of a remarkable triangle point.’ It was eventually called the Lemoine point though he was not actually the first to discover it. Henri Brocard (1845–1922) gave his name to the twin Brocard points, found not by experiment but by solving a published challenge, to find a point O such that the angles OAB, OBC and OCA are equal (Figure
11.7
).
Figure 11.7
Brocard points
 
 
The diagram shows a geometrical construction for one Brocard point: each circle passes through one vertex touching a side there and through a second
vertex. If the angles OAC, OCB and OBA are made equal then we get a second Brocard point.
Soon there was a torrent, a stampede, of new points, lines and circles, identified and classified like specimens in a natural history museum and named after the explorers who discovered them. Joseph Neuberg (1840–1926) gave his name to the
Neuberg
circle, and Christian Nagel (1803–1882), to the
Nagel point
. Ludwig Kiepert (1846–1934) named the
Kiepert
hyperbola, and G. de Longchamps (1842–1906) named the
De Longchamps
point, and so on. However, the rush soon came to an end. As Philip Davis reports, in the comprehensive
Encyklopaedie der Mathematischen Wissenschaften
of 1914 the Modern Geometry of the Triangle was honoured with a hundred-page entry, yet today the subject is (almost) forgotten. Why?
Mathematical explorers can be naturalists fanning across the plains and through the forests, recording everything that they discover, or they can be geologists and geomorphologists, physicists or chemists with their instruments, studying the broad features of the landscape, digging underneath the earth to discover how the terrain was formed, detecting features that are invisible on the surface, attempting to understand the landscape as deeply as possible. Mathematical creativity can be either broad and shallow or deep and profound.
Pythagoras' theorem is deep because it represents a basic feature of the plane surface of Euclidean geometry. Euclid's geometry itself is deep, not only for the wealth of theorems but for the very idea that you can start with just a few assumptions and infer so much from them. The ancient Greeks, whose work Euclid summarised, were the first people to imagine such a possibility.
Euclid's geometry also presented a powerful technique. However, as that technique was better understood and new techniques added – including the
technique of coordinates – the study of Euclidean geometry became more routine, more a matter of merely sound method, and therefore less challenging and less genuinely surprising. The Euler line was a great surprise and so was the nine-point circle, but the Nagel point far less so. There are now literally hundreds of identified ‘special points’ – so they are no longer so special. The great challenges of modern mathematics are now over the hills and far away from triangle geometry.
Figure 11.8
21-point cubic
 
 
And yet, there is a chance that it is already reappearing as a serious subject for research, because thanks to the computer it is now extremely easy to search for new special points and to catalogue their properties, which leaves the mathematician free to ask deeper questions about objects such as the cubic curve in Figure
11.8
, known as the
Neuberg
cubic or
21-point
cubic, because it was originally proved to pass through 21 special points of the triangle, including the vertices of the triangle, the orthocentre, the circumcentre, and the centres of the inscribed and three escribed circles, and the 6 vertices of the equilateral triangles in Napoleon's theorem
.
It is now known to contain many more special points: why so many? It also has many other properties, such as, that the Euler line of the triangle is parallel to the asymptote of the cubic, and so are the tangents at the incentre and excentres. Why?
There are also many other relationships between the special points, many of which are collinear: why? (The answer has to do with group theory.)
There are two distinct ‘Why?’ questions here: the shallow ‘Why?’ can be answered by a straightforward proof which explains how the property follows from more basic facts. The deeper question ‘Why?’ asks why the property
exists in the first place
. We met this distinction when we looked at Pythagoras' theorem. To prove it is relatively easy and can be done in hundreds of ways: to explain why it exists at all is a much subtler, deeper and more important question.
Treated as individual curiosities, most of the special points are not so special but examined as a whole, new questions beg to be answered and new features
are observed and demand to be understood. And that is how mathematics progresses.

Other books

The Erotic Dark by Nina Lane
Veneer by Daniel Verastiqui
The Erection Set by Mickey Spillane
La Tumba Negra by Ahmet Ümit