Games and Mathematics (16 page)
Read Games and Mathematics Online
Authors: David Wells
Infinity and infinite series

Calculus and the idea of a tangent

What is infinity? It's a quintessentially mathematical idea, because the counting numbers go on for ever and we can imagine geometrical space extending for ever, even if that's
physically
impossible. For more than 300 years mathematicians have exploited infinite series, suggesting that they understand ‘infinity’, but it's not so simple.
physically
impossible. For more than 300 years mathematicians have exploited infinite series, suggesting that they understand ‘infinity’, but it's not so simple.
Metaphors for infinity are not game-like and not mathematical. To tame infinity we must bring it down from poetic heaven to solid ground. One way is to interpret it in finite terms, which we can illustrate with this series whose ‘sum’ is ‘obviously’ 1:
 Its sum is ‘obvious’ for several reasons. Here are two, one visual (
Its sum is ‘obvious’ for several reasons. Here are two, one visual (
Figure 8.2
), and one arithmetical.

Figure 8.2
), and one arithmetical.
Figure 8.2
Picture of sum of 2
−
n
Picture of sum of 2
−
n

We have cut off the top half of the square, then the bottom-left quarter, and so on. The terms of the series fill up the square so that the amount left unfilled is as small as we choose. We can reach the same conclusion by arithmetic by calculating the partial sums: the sums of the first 1, 2, 3, 4…terms are,
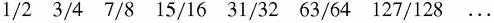
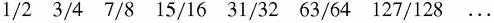
The pattern seems obvious, though perhaps not quite as obvious as the picture. More precisely, the sum of the first n terms of the series is (2
n
− 1)/2
n
and this does get closer and closer to 1 as
n
increases. However, that fact by itself does not quite pin down the idea of an
infinite sum
: after all, it never reaches 1, but is always definitely less – so how can 1 be its sum?
n
− 1)/2
n
and this does get closer and closer to 1 as
n
increases. However, that fact by itself does not quite pin down the idea of an
infinite sum
: after all, it never reaches 1, but is always definitely less – so how can 1 be its sum?
The answer lies, ironically, in changing the meaning of
sum
, in order to
fit the idea
of an
infinite sum
. We agree to use
sum
for a number that the series when summed term by term never actually reaches. That idea is not sharp enough by itself because the term-by-term sum will never reach 100 either, so we add the (imprecise) condition that it gets as ‘close as anything’ to 1. We then make the idea of ‘close as anything’ precise, like this. We suppose that you challenge me with a very small number, say, 1/1000000. To meet the challenge I must show that by adding up enough terms of the series I can make the difference
between the partial sum and 1, less than 1/1 000 000. If I can always meet your challenge, (in this case I can,) then 1 is the sum of the infinite series.
sum
, in order to
fit the idea
of an
infinite sum
. We agree to use
sum
for a number that the series when summed term by term never actually reaches. That idea is not sharp enough by itself because the term-by-term sum will never reach 100 either, so we add the (imprecise) condition that it gets as ‘close as anything’ to 1. We then make the idea of ‘close as anything’ precise, like this. We suppose that you challenge me with a very small number, say, 1/1000000. To meet the challenge I must show that by adding up enough terms of the series I can make the difference
between the partial sum and 1, less than 1/1 000 000. If I can always meet your challenge, (in this case I can,) then 1 is the sum of the infinite series.
The remarkable feature of this definition is that it captures everything that we want to say about the infinite sum being 1, without actually talking about infinity at all! The challenge you set me involves a
finite
number, albeit very small. I answer by showing that a
finite
number of terms will take the partial sum to within less than the number you named. Infinity has vanished, which is one reason why we can be confident that our definition is solid and game-like, rather than vague, poetic and fishy.
finite
number, albeit very small. I answer by showing that a
finite
number of terms will take the partial sum to within less than the number you named. Infinity has vanished, which is one reason why we can be confident that our definition is solid and game-like, rather than vague, poetic and fishy.
Figure 8.3
Parabola
Parabola

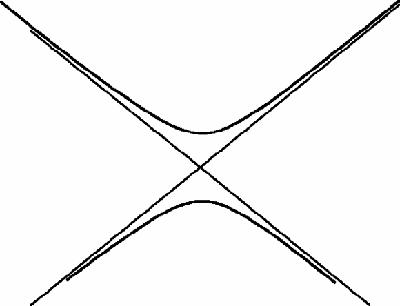
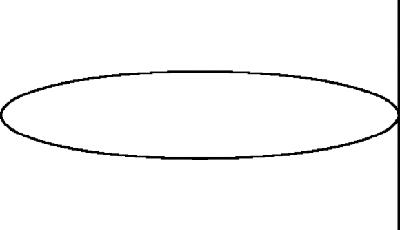
That trick doesn't solve all the problems of infinity by any means. Here is a geometrical puzzle about infinity: of the three conic sections, the ellipse is finite but both the parabola and hyperbola both ‘go off to infinity’ although in seemingly different ways. The parabola (
Figure 8.3
) looks like an ellipse which has been stretched for ever while the hyperbola (
Figure 8.4
) gets closer and closer to its two
asymptotes
as it disappears to infinity.
Figure 8.3
) looks like an ellipse which has been stretched for ever while the hyperbola (
Figure 8.4
) gets closer and closer to its two
asymptotes
as it disappears to infinity.
Figure 8.4
Hyperbola with asymptotes
Hyperbola with asymptotes

How can we formalise these very vague and intuitive ideas? Figure
8.5
is a picture of a parabola
as a closed curve
touching a line. What does this mean? What
should
it mean?
8.5
is a picture of a parabola
as a closed curve
touching a line. What does this mean? What
should
it mean?
Figure 8.5
‘Parabola’ touching line at infinity
‘Parabola’ touching line at infinity

In
projective geometry
, a
line at infinity
is added to the Euclidean plane, containing an infinity of
points at infinity
. The parabola is then a conic which touches the line at infinity at a single real point which is also on its axis, while
the hyperbola, together with its asymptotes, intersects the line at infinity in two distinct real points. (And all circles intersect the line at infinity in the same two
imaginary
points, but that's another story.)
projective geometry
, a
line at infinity
is added to the Euclidean plane, containing an infinity of
points at infinity
. The parabola is then a conic which touches the line at infinity at a single real point which is also on its axis, while
the hyperbola, together with its asymptotes, intersects the line at infinity in two distinct real points. (And all circles intersect the line at infinity in the same two
imaginary
points, but that's another story.)
Tangent
is another easy-to-understand idea that is tricky to pin down. Small children can use a ruler to draw a line which touches a circle but to make it touch ‘exactly’ at a certain point is not so easy. It becomes easier when you realise that the tangent of a circle – by symmetry! – ought to be perpendicular to the radius, but that leaves the problem of drawing accurate tangents to curves like the parabola in
Figure 8.6
.
is another easy-to-understand idea that is tricky to pin down. Small children can use a ruler to draw a line which touches a circle but to make it touch ‘exactly’ at a certain point is not so easy. It becomes easier when you realise that the tangent of a circle – by symmetry! – ought to be perpendicular to the radius, but that leaves the problem of drawing accurate tangents to curves like the parabola in
Figure 8.6
.
Figure 8.6
Parabola with tangent
Parabola with tangent

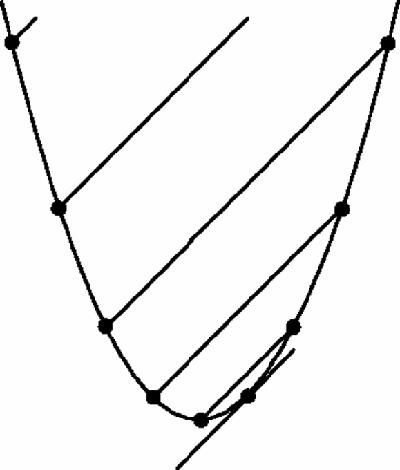
This is the parabola
y
=
x
2
, drawn with horizontal and vertical scales in the ratio 2:1. What is the slope of a tangent touching the curve at (1,1)? Draw the tangent roughly and it seems to be about 2, but drawing is no proof. The set of chords in
Figure 8.7
is also suggestive: they are parallel, they have slope 2 and they appear to be parallel to the tangent at (1,1).
y
=
x
2
, drawn with horizontal and vertical scales in the ratio 2:1. What is the slope of a tangent touching the curve at (1,1)? Draw the tangent roughly and it seems to be about 2, but drawing is no proof. The set of chords in
Figure 8.7
is also suggestive: they are parallel, they have slope 2 and they appear to be parallel to the tangent at (1,1).
Figure 8.7
Parabola with tangent and parallel chords
Parabola with tangent and parallel chords

For another natural hint let's calculate the slopes of the following sequence of regularly spaced chords through (3,9) (
Figure 8.8
).
Figure 8.8
).
Other books
Accent Hussy (It Had 2 B U) by V. Kelly
Saira - TI5 by Heckrotte, Fran
Logan's Story: A Sand & Clay Prequel by Sarah Robinson
The Moonshawl: A Wraeththu Mythos Novel by Storm Constantine
Benjamín by Federico Axat
Scoundrel (Lost Lords of Radcliffe Book 4) by Cheryl Holt
Scarred by Thomas Enger
Ex-Con: Bad Boy Romance by M. S. Parker, Shiloh Walker
The Letter by Sylvia Atkinson
Callsign: King II- Underworld by Robinson, Jeremy