Games and Mathematics (19 page)
Read Games and Mathematics Online
Authors: David Wells
Weird objects and mysterious situations
A practical use for divergent series
Divergent series – the harmonic series was the first and simplest of many – may be amusing curiosities but if they have no sum, what use can they be? One response to the paradox was to abandon them as best avoided, which is exactly what some early modern mathematicians did. Fearful of getting wrong answers, they shied away.
Euler, however, was not deterred. He set his course boldly straight ahead and produced typically astonishing results. Indeed,
astonishing
is hardly the word,
absurd
might seem a better adjective. Yet Euler kept going because the results he got were consistent, they made some kind of sense, and so he understood his problem as working out the meaning of divergent series
. Let's see what happened in practice, starting with a very simple series that oscillates. The series,
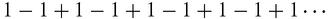 can be seen as, (1 − 1) + (1 − 1) + (1 − 1) + (1 − 1) + ⋯
can be seen as, (1 − 1) + (1 − 1) + (1 − 1) + (1 − 1) + ⋯
astonishing
is hardly the word,
absurd
might seem a better adjective. Yet Euler kept going because the results he got were consistent, they made some kind of sense, and so he understood his problem as working out the meaning of divergent series
. Let's see what happened in practice, starting with a very simple series that oscillates. The series,
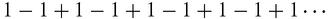
which is apparently zero, but also as,
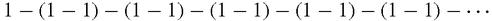 which seems to be 1. Leibniz argued that since the partial sums when you start adding up the terms from the start, are 1, 0, 1, 0, 1, 0…with equal probability, then the sum ‘should be’ 1/2. This certainly shows imagination in bringing chance and probability into the sum of a fixed series [Kline
which seems to be 1. Leibniz argued that since the partial sums when you start adding up the terms from the start, are 1, 0, 1, 0, 1, 0…with equal probability, then the sum ‘should be’ 1/2. This certainly shows imagination in bringing chance and probability into the sum of a fixed series [Kline
1983
: 308].
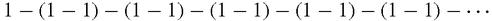
1983
: 308].
Guido Grandi, a mathematician who was also a Jesuit priest, drew a different and mystical conclusion from this ‘demonstration’ that 0 = 1: it showed mathematically, he claimed, how the world could have been created from nothing [Knopp
1928
: 133n].
1928
: 133n].
Euler was smarter, and more mathematically imaginative: he took the series,
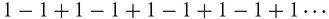 and compared it to the series we have already met:
and compared it to the series we have already met:
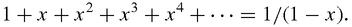
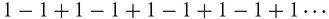
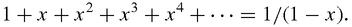
Putting
x
= −1, he concluded that the sum of the first series ought to be 1/2, which agrees with Leibniz but still seems absurd. James Bernoulli in 1696 described it as a ‘not inelegant paradox’. It was indeed, but paradoxes exist to be explained and Euler's basic idea that you should interpret divergent series as specific values of a function was profound and extremely powerful. Euler had confidence in his own judgement and intuition, and went on to conclude that,
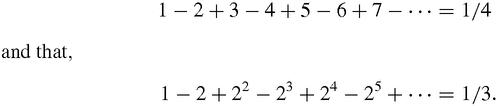
x
= −1, he concluded that the sum of the first series ought to be 1/2, which agrees with Leibniz but still seems absurd. James Bernoulli in 1696 described it as a ‘not inelegant paradox’. It was indeed, but paradoxes exist to be explained and Euler's basic idea that you should interpret divergent series as specific values of a function was profound and extremely powerful. Euler had confidence in his own judgement and intuition, and went on to conclude that,
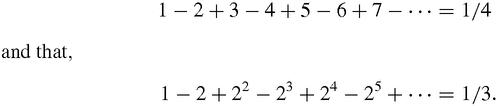
In a later paper,
On Divergent Series
(
1760
) he discussed what it means to find the ‘sum’ of a series and promised ‘to clarify a concept causing up to now the greatest difficulties’ [Barbeau
1979
: 357]. He then looked at the series,
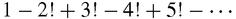 With typical imagination and consistency rather than rigour, he used several different methods to get different results for its sum, including 0.580, 0.60542, and 0.59966 [Barbeau
With typical imagination and consistency rather than rigour, he used several different methods to get different results for its sum, including 0.580, 0.60542, and 0.59966 [Barbeau
1979
: 357] [Euler
1760
a].
On Divergent Series
(
1760
) he discussed what it means to find the ‘sum’ of a series and promised ‘to clarify a concept causing up to now the greatest difficulties’ [Barbeau
1979
: 357]. He then looked at the series,
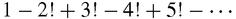
1979
: 357] [Euler
1760
a].
These results differ, but not absurdly – and Euler had used ingenious approximations on the way. If his arguments were genuinely nonsensical, would he have got such comparable figures? That's most unlikely! The interpretation of
his results was another matter, and it took over a hundred years for consistent and satisfactory interpretations of divergent series to be accepted.
his results was another matter, and it took over a hundred years for consistent and satisfactory interpretations of divergent series to be accepted.
Euler well knew that his ‘sum’ of a divergent series was no ordinary sum, as adapted to fit infinite series. He was deliberately changing the meaning of the word. He did so because using his new conception, his ‘experimental’ evidence was sufficiently convincing. Not surprisingly, Euler's repeated boldness led to occasional mistakes but this was not one of them and his successes far outweighed his failures. As Morris Kline puts it,
Like his predecessors, Euler's work lacks rigour, is often
ad hoc
, and contains blunders, but despite this, his calculations reveal an uncanny ability to judge when his methods might lead to correct results.
The exploration of mathematical miniature worlds is deeply scientific – and can therefore leave mathematicians suspended in uncertainty for long periods, like any scientist. The idea that 1 − 1 + 1 − 1 + 1 − 1….. = 1/2 is either simple-minded, a silly suggestion only a child or a mystic would make, or it is the brilliant intuition of a great mathematician (Leibniz) or the clear and logically satisfying result of deep insight into what the terms ‘convergence’ and ‘divergence’ could and should mean, once you decide you cannot lose the aesthetic delights and practical applications of series that on the face of it are pathologically absurd and dangerous.
This process of developing your idea of what an entity
ought
to be, closely parallels the physicists’ development of the concept of an atom or an electron, or the wave–particle model of light. The final results of mathematical exploration are pelucidly clear but on the way they can be confusing and messy. Fortunately, they are exciting too.
ought
to be, closely parallels the physicists’ development of the concept of an atom or an electron, or the wave–particle model of light. The final results of mathematical exploration are pelucidly clear but on the way they can be confusing and messy. Fortunately, they are exciting too.
Euler himself illustrated one use of divergent series. First he proved that,
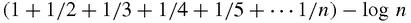 tends to a limit, known as Euler's constant, or γ for short. Euler then found a series for γ:
tends to a limit, known as Euler's constant, or γ for short. Euler then found a series for γ:
 where the Bs are the Bernoulli numbers. Unfortunately, this series for γ diverges: fortunately, it has the remarkable property that the error from stopping
where the Bs are the Bernoulli numbers. Unfortunately, this series for γ diverges: fortunately, it has the remarkable property that the error from stopping
at any particular term
is less than the next term in the series
. Since the early terms get very small indeed before the later terms get larger, Euler was able to use just the first 10 terms of the series to show that,
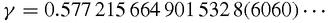 Gauss, another walking calculator, went rather further than Euler and added the last four figures in parentheses [Bromwich
Gauss, another walking calculator, went rather further than Euler and added the last four figures in parentheses [Bromwich
1931
: 324–5]. What a wonderful demonstration that the road to insight and understanding in mathematics must pass through the gates of imagination!
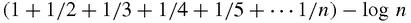

at any particular term
is less than the next term in the series
. Since the early terms get very small indeed before the later terms get larger, Euler was able to use just the first 10 terms of the series to show that,
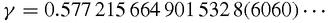
1931
: 324–5]. What a wonderful demonstration that the road to insight and understanding in mathematics must pass through the gates of imagination!
Other books
Don't You Love Your Daddy? by Sally East
From the Notebooks of Melanin Sun by Jacqueline Woodson
The Julian Game by Adele Griffin
The Knaveheart's Curse by Adele Griffin
The Secrets of Tree Taylor by Dandi Daley Mackall
The Violent World of Michael Shayne by Brett Halliday
The Infernal Devices 01 - Clockwork Angel by Cassandra Clare
Family of the Heart by Dorothy Clark
The Odin Mission by James Holland