Games and Mathematics (14 page)

 

 

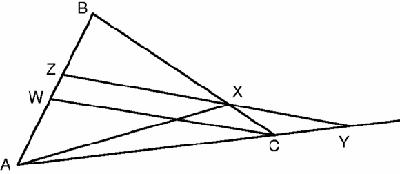
We now change the first two ratios into ratios on the side AB:
We now multiply the three ratios: AZ/ZW · WZ/ZB · BZ/ZA = 1.

Another elegant theorem about transversals concerns a triangle within a circle and a point P on its circumference (
Figure 7.6
).

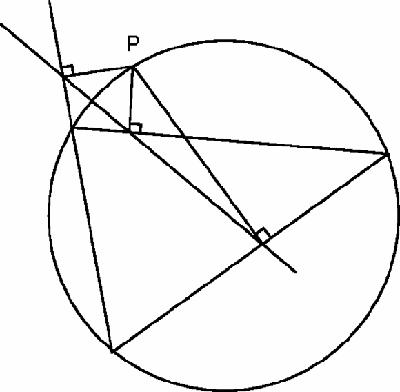
We drop perpendiculars from P to each side of the triangle. The feet of the perpendiculars lie on a straight line. The simplest proof uses two basic circle properties, that angles in the same segment are equal and that if a quadrilateral has opposite angles which sum to 180
^o
, then its vertices lie on a circle.

The converse of Simson's theorem is also true: if a line traverses the sides of a triangle and the perpendiculars at the points of intersection are concurrent at P, then P lies on the circumcircle. We shall meet this theorem again.

The only curve that Euclid
considered was the ‘perfect’ circle which because it is so simple and symmetrical has many equally simple and elegant properties. The parabola has good claims to be the next simplest curve and we can deduce several of its properties using basic Euclidean properties of triangles, (and sometimes of circles also), plus its own definition and starting with an intuitively convincing but imperfectly logical
dynamic
argument.

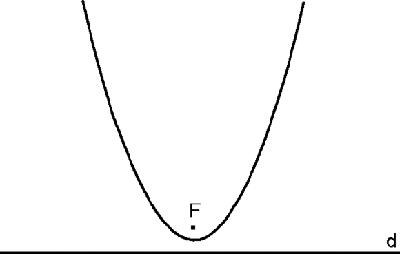
The parabola is the path of a point which moves so that it is always the same distance from a point F, called the focus, and a line d, called the directrix:
Figure 7.7
shows a basic parabola.

Now let's draw a tangent (
Figure 7.8
). Think of the point P actually moving along the tangent in the direction of the arrow: since it is equidistant from F and d and moving momentarily so as to remain so, the tangent bisects the angle

 

 

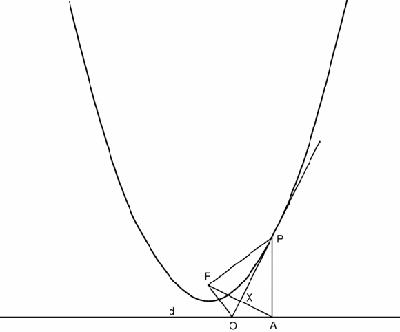
FPA. This physical argument, of a kind Archimedes favoured, gives us our first basic angle property. It means that the triangles FPX and APX are congruent, and X is the mid-point of FA and AO = FO, and the perpendicular from F to the tangent at P meets the directrix at A. Since the vertex of the parabola (its lowest point) is halfway between F and d, it follows that X, the foot of the perpendicular from F to the tangent at P, lies on the tangent at the vertex (
Figure 7.9
).

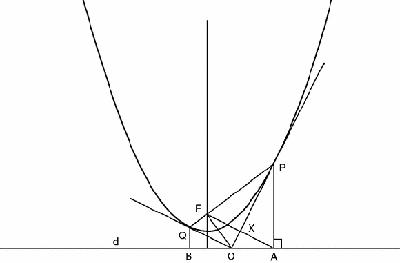
Now complete the chord through F, add the tangent at Q, and mark B so that FO = AO = OB. Then since FQ = QB by definition, FOBQ is a kite, OQ is a line of symmetry and so OQ is the tangent at Q.

Also, since AO = OF = OB, AFB is a right angle. Since APF + BQF = 180, OPF + OQF = 90° and so POQ is a right angle also.

It turns out, typically, that the figure formed by the parabola, the two tangents and lines of equal length from F and to d is extremely simple. It illustrates a basic structure that is forced by the definition and basic Euclidean properties – but this is only the start: any number of other properties can be discovered, and proved, starting from the parabola's extremely simple definition. One more is shown in
Figure 7.10
.

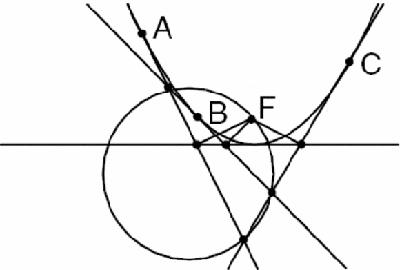
We first add a third tangent, so that the three tangents at A, B and C form a triangle. Next we draw the circumcircle of this triangle. The perpendiculars
from the focus F will all lie a straight line, the tangent at the vertex, and so by the
converse
of Simson's theorem, F lies on the circle too.

It is typical that the apparently idiosyncratic Simson's theorem can be used to prove a theorem about parabola
s. Euclid
ean geometry and all its relations are intimately linked together and repeatedly refer to each other. (We can also add that our original
dynamic
argument that the tangent bisects FPA must be correct
in some sense
, to produce such a simple, rich structure.)

We conclude with a new perspective on the parabola and the other conics that was found 2000 years after Euclid in 1822, after being missed first by Euclid and then by Apollonius and a host of other geometers.

The
conics were originally studied by the ancient Greeks as slices of a circular cone which is the meaning of
conic
(
Figure 7.11
).

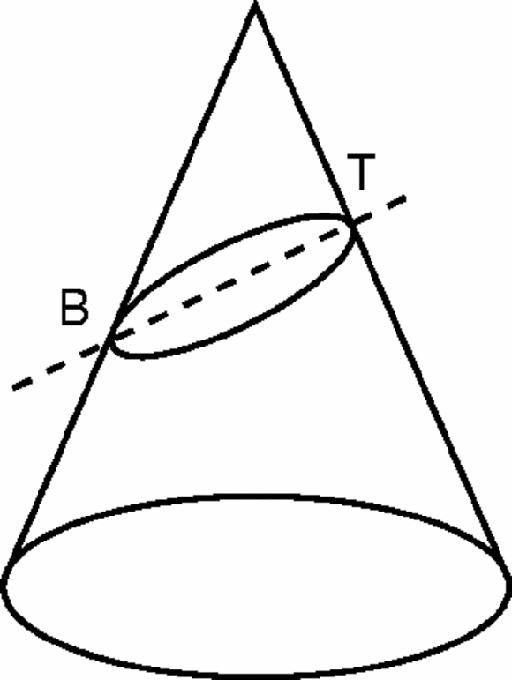
An immediate puzzle is why this asymmetrical slice should produce a symmetrical ellipse. At first sight you might think that the slice will be wider at the bottom end B, because the cone is ‘larger’ further down. On second thoughts, you might think that it would be wider at the top, at T, because there the slice
cuts the edge at a larger angle. Neither of these speculations is correct: the elliptical cross-section is completely symmetrical.

A further puzzle is: what is the connection between the foci and directrices of a conic and the slice of the cone which creates the conic?

This was answered, rather late in the day, by Germinal Pierre Dandelin (1794–1847) who discovered a surprising way of finding the focus and directrix by constructing the two spheres that touch the cone along a circle and the plane of the conic (one sphere on either side of the cutting plane for the ellipse) in two single points (Figure
7.12
). The figure, once again, looks asymmetrical but no, the two points of contact turn out to be the foci, and the directrices are the lines in which the plane of the elliptical slice meets the planes through the circles along which each sphere touches the cone.

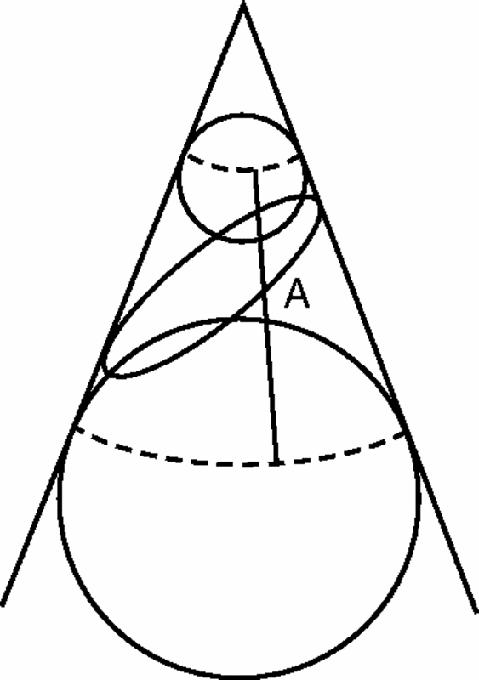
The line through A is a generator of the cone touching both spheres on their circles of contact. The line from A to the focus on either sphere is equal in length to that part of the segment, from which it follows that the total distance from A to both foci is constant.

Truly, the consequences of Euclid's geometrical game are endless!