Games and Mathematics (17 page)
Read Games and Mathematics Online
Authors: David Wells
Figure 8.8
Parabola with chords through one point
Parabola with chords through one point
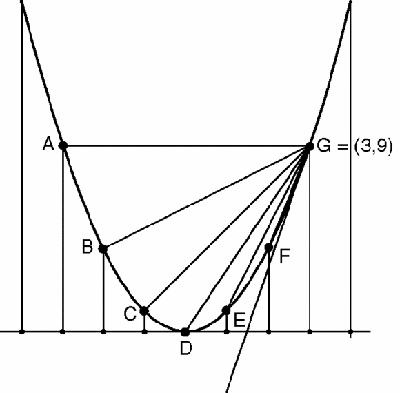
The sequence of chords from AG to GG have slopes,
which strongly suggests that the tangent – which ‘joins the point (3,9) to itself’ – should have slope exactly 6, but how can we ‘prove’ this? Once again, we need a definition that matches the situation.
AG | BG | CG | DG | EG | FG | ‘GG' |
0 | 1 | 2 | 3 | 4 | 5 | ? |
The slope of the chord joining (3,9) to (
t
,
t
2
) is,
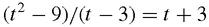 by basic algebra, so when
by basic algebra, so when
t
= 3, the slope will indeed be 6. In other words, we imagine the chord rotating as (
t
,
t
2
) moves closer and closer to (3,9) until
in the limit
the chord doesn't actually exist because you can't draw a line joining a
point to itself, but the slope of the chord
in the limit
is 6. Then we take the final deliberate step and
define the tangent
to be the line through (3,9) with slope 6.
t
,
t
2
) is,
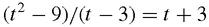
t
= 3, the slope will indeed be 6. In other words, we imagine the chord rotating as (
t
,
t
2
) moves closer and closer to (3,9) until
in the limit
the chord doesn't actually exist because you can't draw a line joining a
point to itself, but the slope of the chord
in the limit
is 6. Then we take the final deliberate step and
define the tangent
to be the line through (3,9) with slope 6.
Notice all the steps in this process: we start with children making actual physical experiments complete with inevitable experimental errors, on the understanding that a tangent is a straight line that ‘touches’ a curve, whatever that means; we move on to a parabola and our own calculations of the slopes of chords, still without any clear idea of what a ‘tangent’ is or ‘ought to be’; finally, we get a simple answer that ‘makes sense’ and answers all our doubts – and we then turn round and
define
a tangent to be the answer we got!
define
a tangent to be the answer we got!
This is not a circular argument because we haven't actually gone round in a circle. Rather, we started like a detective with some strong clues as to the kind of object a tangent ought to be. We experimented to find more clues, and finally we had enough clues to point us with confidence towards the solution.
Actually, this is not the only possible definition. Let's go back to the parallel chords which are indeed parallel to the tangent. These chords all meet the parabola in two distinct points. If we recall that algebraic equations – including quadratics – can have double as well as single roots, then we might hope that the tangent at (3,9) will prove to have a double intersection with the parabola at that point. The equation of the line through (3 −
t
, (3 −
t
)
2
) and (3 +
t
, (3 +
t
)
2
) is,
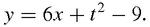
t
, (3 −
t
)
2
) and (3 +
t
, (3 +
t
)
2
) is,
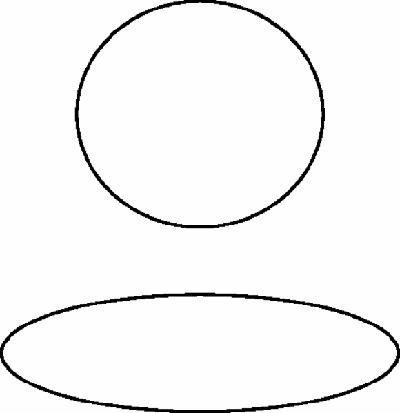
This will intersect
y
=
x
2
when
x
2
− 6
x
+ (9 −
t
2
) = 0 and this does indeed have a double root when
t
= 0, as expected. Once again, we are home and dry because all these chords have slope 6 so they are parallel, and they turn out to be parallel to the tangent at (3,9), according to our
second new definition
which defines the tangent algebraically without talking about limits at all: the tangent at (3,9) is the line which when we solve the equation to find where it meets the parabola, gives a double root.
y
=
x
2
when
x
2
− 6
x
+ (9 −
t
2
) = 0 and this does indeed have a double root when
t
= 0, as expected. Once again, we are home and dry because all these chords have slope 6 so they are parallel, and they turn out to be parallel to the tangent at (3,9), according to our
second new definition
which defines the tangent algebraically without talking about limits at all: the tangent at (3,9) is the line which when we solve the equation to find where it meets the parabola, gives a double root.
(This doesn't explain why there could not be more than one tangent at one point: occasionally there is. We also need to prove that these two definitions of a tangent usually give the same answer and to understand any exceptional cases when they do not.)
Mathematical textbooks are much more precise in defining a tangent than we have been: a
general
definition must apply to a
general
curve, or at least a wide class of curves that ideally includes all the curves we are interested in. Are there ‘curves’ for which these definitions don't work? Yes, there are weird ‘curves’ which seem hardly ‘curves’ at all because they do not have tangents. Naturally, mathematicians have investigated them also – and so maths moves on, ever forwards and upwards!
general
definition must apply to a
general
curve, or at least a wide class of curves that ideally includes all the curves we are interested in. Are there ‘curves’ for which these definitions don't work? Yes, there are weird ‘curves’ which seem hardly ‘curves’ at all because they do not have tangents. Naturally, mathematicians have investigated them also – and so maths moves on, ever forwards and upwards!
Will the informal and psychologically powerful concept of infinity ever be completely tamed? Plausibly not, because ideas of infinity – ‘ideas’ in the plural – turn up so often in so many different parts of the mathematical landscape.
of a parabola?
We conclude by looking at another example of a familiar term being less clear than we suppose, also illustrated by the parabola.
The idea of ‘shape’ might seem pretty unproblematic. All circles are obviously the same shape, all squares are the same shape, all triangles are not, and parabolas and ellipses vary from narrow to broad or from nearly-circular to long and narrow (
Figures 8.9
and
8.10
).
Figures 8.9
and
8.10
).
Figure 8.9
Two parabolas, different ‘shapes’
Two parabolas, different ‘shapes’

Figure 8.10
Two ellipses, different ‘shapes’
Two ellipses, different ‘shapes’
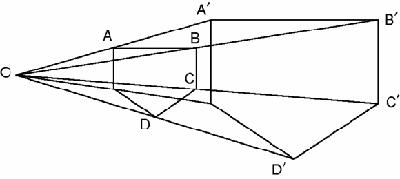
It is also easy to convince yourself by experiment, or reasoning with a diagram on a square grid, that if you ‘blow up’ a figure from a
centre of
similarity
, O, the new figure has the same shape. The pentagon in
Figure 8.11
has been ‘blown up’ by a factor of 2, meaning that each new point, A’, B’, C’…is twice times as far from O as its original point.
centre of
similarity
, O, the new figure has the same shape. The pentagon in
Figure 8.11
has been ‘blown up’ by a factor of 2, meaning that each new point, A’, B’, C’…is twice times as far from O as its original point.
Figure 8.11
Two pentagons in perspective
Two pentagons in perspective
The claim, however, that parabolas vary from narrow to broad is quite misleading and illustrates how even apparently simple ideas like
shape
must be treated with kid gloves. There is a case for arguing – against first appearances – that
all parabolas
are the same shape.
shape
must be treated with kid gloves. There is a case for arguing – against first appearances – that
all parabolas
are the same shape.
Figure 8.12
Two parabolas with ‘matching’ chords
Two parabolas with ‘matching’ chords

In
Figure 8.12
one parabola has been blown up by a factor of 2, from its vertex, to create 6 new points, plus the original vertex, lying on a new parabola. According to our previous argument the resulting figure ought to be same shape. Indeed, the resulting 7 points do lie on another parabola which seems, however, to be ‘wider’ than the original parabola. So is it the same shape or not?
Figure 8.12
one parabola has been blown up by a factor of 2, from its vertex, to create 6 new points, plus the original vertex, lying on a new parabola. According to our previous argument the resulting figure ought to be same shape. Indeed, the resulting 7 points do lie on another parabola which seems, however, to be ‘wider’ than the original parabola. So is it the same shape or not?
Searching for a decisive perspective we can resort to the equation of the parabola,
y
=
ax
2
. Changing
y
and
x
by the same factor c, so that the shape is unchanged, we get the equation
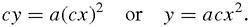
y
=
ax
2
. Changing
y
and
x
by the same factor c, so that the shape is unchanged, we get the equation
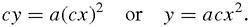
Since
c
can be any number, it does seem that any two parabolas,
y
=
ax
2
and
y
=
acx
2
have the same shape
. Still not convinced? Then let's draw the
same portion
of the ‘narrow’ and ‘broad’ parabolas next to each other. Now they do look genuinely to be the same shape
but of different sizes
which is a clue to what is happening. The whole of any parabola can be mapped on to the whole of any other parabola, by expanding one or contracting the other. So whole-parabolas are all the same shape but parts-of-parabolas are not the same shape (
Figure 8.13
).
c
can be any number, it does seem that any two parabolas,
y
=
ax
2
and
y
=
acx
2
have the same shape
. Still not convinced? Then let's draw the
same portion
of the ‘narrow’ and ‘broad’ parabolas next to each other. Now they do look genuinely to be the same shape
but of different sizes
which is a clue to what is happening. The whole of any parabola can be mapped on to the whole of any other parabola, by expanding one or contracting the other. So whole-parabolas are all the same shape but parts-of-parabolas are not the same shape (
Figure 8.13
).
Figure 8.13
Two parabolas with matching points
Two parabolas with matching points
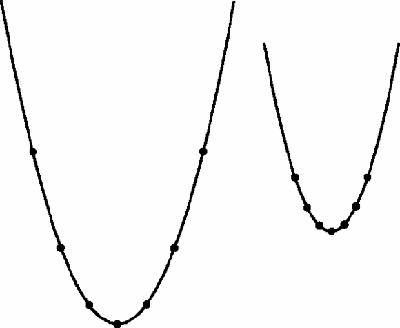
Conversely, we can easily find parts of two rectangles, however different their whole-shapes, that are the same shape. The square and rectangle in
Figure 8.14
are obviously not the same shape, but the parts cut off below are similar.
Figure 8.14
are obviously not the same shape, but the parts cut off below are similar.
Figure 8.14
Two rectangles
Two rectangles
If even
shape
is not such a simple idea what other everyday ideas might prove to be mathematically tricky?
shape
is not such a simple idea what other everyday ideas might prove to be mathematically tricky?
Other books
Fiend by Harold Schechter
The Dead Won't Die by Joe McKinney
The Choice by Bernadette Bohan
Handsome Brute: The True Story of a Ladykiller by O'Connor, Sean
Moonlight(Pact Arcanum 3) by Arshad Ahsanuddin
Caught by the Sea by Gary Paulsen
Raisin Rodriguez & the Big-Time Smooch by Judy Goldschmidt
To the End of the War by James Jones
Moyra Caldecott by Etheldreda
The Mambo Kings Play Songs of Love by Oscar Hijuelos