Games and Mathematics (7 page)
Read Games and Mathematics Online
Authors: David Wells
Chess and other abstract games are created by men (and occasionally by women) but their creation has implications which are very hard to grasp. When a player has an original idea for an opening move, it may seem like his own idiosyncratic invention, but if it turns out to be sound then the invention becomes a discovery of an effective plan. The rules of an abstract game may be very simple, yet their implications may be unfathomable. Our human creativity includes the ability to illuminate the obscure – but also to create the obscure.
The same turns out to be true of mathematics though with a subtle twist. If a mathematician believes he has discovered some new theorem, but it turns out to be untrue, then naturally he thinks of the erroneous proof as something he invented, which didn't work, like a mechanical device that was built to perform a certain function but failed to do so. But if it turns out to be true, then there is a strong feeling that it has actually just been discovered. This is how Richard Hamming puts it, referring to his own mathematical research:
When I try to examine my own beliefs…I find that if the result seems to be important then I found it, but if it seems to be rather trivial, then I created it!
Go is an extremely ancient oriental game much played in Japan, China and Korea. The best players in Japan, equivalent to our chess
grandmasters, are well-paid professionals who earn as much as top Western golfers. Their games are followed by devoted fans and their services sought by eager businessmen for whom a high amateur grade is a status symbol.
grandmasters, are well-paid professionals who earn as much as top Western golfers. Their games are followed by devoted fans and their services sought by eager businessmen for whom a high amateur grade is a status symbol.
The standard board which is 19 lines by 19 lines (smaller boards, 13 by 13 or 9 by 9, are used when teaching beginners) starts empty, and players place a single stone, either black or white, alternately, on an intersection of two lines, with the object of surrounding territory or their opponent's stones.
In
Figure 2.11
, the players are sketching out positions in the corners of the board: in Go, the edges are used as a defence, and in the opening the corners where you are protected by two edges are crucial.
Figure 2.11
, the players are sketching out positions in the corners of the board: in Go, the edges are used as a defence, and in the opening the corners where you are protected by two edges are crucial.
Go has a far larger board than chess but much simpler ‘moves’. The result is another rich game that lies near the boundary of whatever the human mind can master. It might seem that Go is a ‘mathematically’ simple game because its rules are so simple, but no, the board is so large and there are so many possible moves at each turn that Go players rely even more than chess players on strategical judgement and intuition, as well as tactical calculation.
The Japanese Rules of GoThis is a simple version. The official rules complete with explanatory notes are at:
www.cs.cmu.edu/∼wjh/go/rules/Japanese.html
on which this epitome is based.Two players compete on a board, to see which can take more territory.The board is a grid of 19 horizontal and 19 vertical lines forming 361 intersections. A stone can be played on any unoccupied intersection.The board is initially empty.The players can alternately play one move at a time, one player playing the black stones, his opponent the white stones.After a move is completed, a group of stones belonging to one player exists as long as it has a horizontally or vertically adjacent empty point, called a ‘
liberty
’.If, after a player's move, a group of his opponent's stones has no liberties, the player removes all these stones, as
prisoners
.A shape in which the players can alternately capture and recapture one opposing stone is called a ‘
ko
’. A player whose stone has been captured in a ko cannot recapture in that ko on the next move.A group of stones which cannot be captured by the opponent is alive. A group which can be captured is dead.Empty points surrounded by the live stones of just one player are called ‘
eye points
’. Other empty points are called ‘
dame
’. Stones which are alive but only possess dame are said to be in ‘
seki
’.Eye points surrounded by stones that are alive but not in seki are called ‘
territory
’, each eye point counting as one point of territory.When a player passes his move and his opponent passes in succession, the game stops.After agreement that the game has ended, each player removes any opposing dead stones from his territory and adds them to his prisoners.Prisoners are then placed in the opponent's territory, and the remaining points of territory are counted. The player with more territory wins.If both players have the same amount the game is a draw, which is called a ‘
jigo
’.
Like chess pieces, the pieces at Go can also take any form. When I learned to play in the 1960s good stones and boards were hard to come by in the West so we used a kind of sugared almond, painting half of them black. The shape was close to Japanese standard stones which are made of shell or slate, but the
weight, colour and feel were not right, but that mattered not at all because we
used
them as Go stones, so they
were
Go stones. This also works the other way round. When John Horton Conway was inventing the Game of Life with no computer to aid him, he used Go stones on a Go board to represent the state of the ‘game’.
weight, colour and feel were not right, but that mattered not at all because we
used
them as Go stones, so they
were
Go stones. This also works the other way round. When John Horton Conway was inventing the Game of Life with no computer to aid him, he used Go stones on a Go board to represent the state of the ‘game’.
Figure 2.11
Opening position of Go game
Opening position of Go game
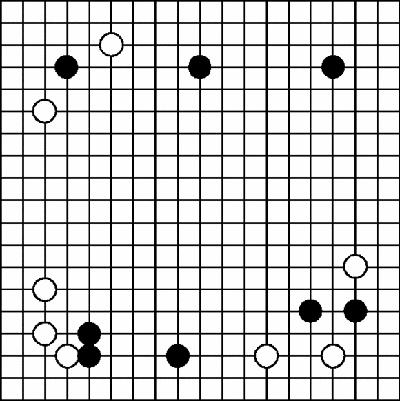
Because the Go board is so large that players have to rely more on intuition and judgement than chess players, efforts by artificial intelligence enthusiasts to program computers to play Go have been disappointing.
The original game of choice for the Artificial Intelligence community was chess. In 1957, Herbert Simon, pioneer of cognitive psychology and artificial intelligence and later a winner of the Nobel prize for economics, predicted that a computer would be world chess champion within ten years. A bizarre blunder, based on the naive idea that computers would soon be able to imitate the thought processes of the human brain whose complexity Simon grossly underestimated.
Forty
years later, Gary Kasparov did lose a game to the computer program Deep Blue
but it did not play in the style of a human player. The artificial intelligence of Deep Blue was just that – artificial – and the goal of simulating the workings of the human mind proved much further away than Simon and his colleague Alan Newell realised [Wells
2003
: 159–60].
Forty
years later, Gary Kasparov did lose a game to the computer program Deep Blue
but it did not play in the style of a human player. The artificial intelligence of Deep Blue was just that – artificial – and the goal of simulating the workings of the human mind proved much further away than Simon and his colleague Alan Newell realised [Wells
2003
: 159–60].
Computer analysis of Go lags even further behind and there is no prospect in the near future of a Go program beating a top professional. From 1985 to 2000 when it lapsed, a prize of $1000000 was offered by Acer Incorporated and the Ing Chang-Ki Wei-Chi Educational Foundation for the first Go program to beat a Go professional. No way! The current strongest Go
programs are about 10
kyu
level or 10 grades below the basic amateur sho-dan level which any player is traditionally supposed to reach after playing ‘one thousand games’. So vastly better is the human brain at spotting patterns and developing intuition and a ‘feel’ for the game, than the most powerful of today's supercomputers.
Combinatorial game theory (CGT)Some games are so simple, unlike chess and Go, that they can actually be solved completely by mathematical arguments. Nim is the most famous example. Your start with several piles of stones or other objects. Players take turns to select one of the piles and take any number of the objects in it, from a single object to the whole pile. Two rules exist for deciding the winner. Either the winner is the player who does
not
take the last object, or the player who does.Nim was completely ‘solved’ by Charles Bouton in 1901, meaning that he showed which player should win, given a certain set of piles to start with, and how that player should play to guarantee the win. Like the Tower of Hanoi
, the solution involves binary numbers.Nim has the important feature, shared with all the games we have presented, that the position is completely open to both players, unlike card games or poker-type games whose analysis therefore involve probabilities. The latter have been analyzed by mathematical game theory which has been applied to economic competition between firms, a nuclear arms race, the sale of licences for mobile phones operators and other more-or-less realistic scenarios.Nim is important for another reason. In the 1930s Roland Sprague and Patrick Grundy proved independently that all impartial games – meaning that for every position of the game, the same moves are available to both players – are equivalent to some game of nim, so the variety of impartial games is less than it might seem.The extraordinary book,
Winning Ways for Your Mathematical Plays
, by John Horton Conway, the inventor of the game of Life, and his colleagues Elwyn Berlekamp and Richard Guy [Berlekamp, Conway & Guy
1982/2001
] showed how some very simple games which were not impartial – but not including chess and Go which are far too complex – could also be solved mathematically.Conway was inspired in his early work on combinatorial games by the endgame at Go which, as we shall see, is much more mathematical than the rest of the game, so it is appropriate that one of the highlights of subsequent work on CGT was
Mathematical Go: Chilling Gets the Last Point
by Elwyn Berlekamp and David Wolfe [Berlekamp & Wolfe
1994
] which reduces the final stages of any Go game to a (complex) calculation.
kyu
level or 10 grades below the basic amateur sho-dan level which any player is traditionally supposed to reach after playing ‘one thousand games’. So vastly better is the human brain at spotting patterns and developing intuition and a ‘feel’ for the game, than the most powerful of today's supercomputers.
However, the endgame at Go
in which the board is separated into regions, often relatively small, which no longer interact, is quite another matter. Using
Combinatorial Game Theory
, the end game of Go can be treated as a collection of solvable sub-games. We might say that the opening and middle game of Go are less mathematical than chess, but the endgame is much more mathematical. So, fortunately for the millions of players of chess and Go, although the ‘Fundamental Theorem of Combinatorial Game Theory
’ says that,
in which the board is separated into regions, often relatively small, which no longer interact, is quite another matter. Using
Combinatorial Game Theory
, the end game of Go can be treated as a collection of solvable sub-games. We might say that the opening and middle game of Go are less mathematical than chess, but the endgame is much more mathematical. So, fortunately for the millions of players of chess and Go, although the ‘Fundamental Theorem of Combinatorial Game Theory
’ says that,
Every game of perfect information is either unfair (one player has a winning strategy) or boring (two rational players will always bring about a draw
the qualification
rational
is so strict and so severe that no two real human players, however skilful, can ever be totally rational, and so chess and Go are not, after all, boring.
rational
is so strict and so severe that no two real human players, however skilful, can ever be totally rational, and so chess and Go are not, after all, boring.
The games of Nine Men's Morris, Hex, chess and Go vary in complexity and subtlety, and in popularity. The hardest, chess and Go, because they offer the greatest challenge and the greatest psychological rewards in terms of beauty and elegance, are the most popular, but they are the least accessible to mathematical treatment.
What other games might be invented in the future? A game on the lines of Nine Men's Morris could be invented by any alien civilisation on a distant planet and the chess board pattern must be discovered by intelligent life elsewhere in the universe and games may be played on it, even a game modelling two opposing armies, though they are hardly likely to invent Western chess. Hex, so simple and so
non-arbitrary
might actually exist ‘out there’. If it does, then it is likely that players on Planet Zorg will also have decided that playing on very small boards is uninteresting and that too-large boards are unplayable, and they may well know the same proof that white ought to win – just as we expect them to have much the same mathematics that we do. They might also have analysed the game much further than we have.
non-arbitrary
might actually exist ‘out there’. If it does, then it is likely that players on Planet Zorg will also have decided that playing on very small boards is uninteresting and that too-large boards are unplayable, and they may well know the same proof that white ought to win – just as we expect them to have much the same mathematics that we do. They might also have analysed the game much further than we have.
It is in the nature of games that they have the potential to be more-or-less universal, one of many mysterious connections between mathematics and abstract games to which we now turn.
3
Mathematics and games: mysterious connections
Can you ‘look ahead’?
out in words, which is
not usually
how it is thought through by the player, a very short sequence might go something like this:
A novel kind of object
communicated. I once wrote the introduction to a book on aesthetics and mathematics by a Chinese author, Professor Wu Kai-Lang. Flipping the pages today, I grasp not a single Chinese character but I can read the mathematical statements because they use Arabic numerals and the usual symbols, a part of the universally shared language of mathematics.
They are abstract
Mathematics and games: mysterious connections
There are so many connections between games and maths that it is no wonder that many mathematicians play chess or Go or Bridge, or that so many abstract game players are into mathematics.
The presence of rules or underlying assumptions, the fact that expert chess players can play games in their heads, just as most people can do at least some calculations in their heads and maybe visualise a cube sliced symmetrically into two parts; the fact that there are tactics and strategies for solving problems in chess and mathematics; the confidence that we – often but not always! – feel that our conclusions are correct, that we can
prove
them, and the reliance of the chess player and mathematician on patterns and structure – these shared features all point to deep underlying connections between mathematics and abstract games. Let's start with perhaps the most remarkable of all – that they can both ‘in theory’ be done in the mind.
Games and mathematics can be analysed in the head…prove
them, and the reliance of the chess player and mathematician on patterns and structure – these shared features all point to deep underlying connections between mathematics and abstract games. Let's start with perhaps the most remarkable of all – that they can both ‘in theory’ be done in the mind.
…provided we make allowances for limitations of memory and visualisation. Few of us have Euler's phenomenal memory. On the other hand, even first-school children are expected by their teachers to do simple sums by ‘mental arithmetic’ and all strong chess players can informally discuss a game they have just played with limited recourse to the board.
Of course, you can
imagine
doing many activities in your head: sports psychologists recommend that champion sportsmen mentally rehearse their next high jump or ski run as an aid to better performance but that mental action is only
in imagination
. Euler and Koltanowski
, however, were not imagining they were mentally creating mathematics and playing chess – they really were.
imagine
doing many activities in your head: sports psychologists recommend that champion sportsmen mentally rehearse their next high jump or ski run as an aid to better performance but that mental action is only
in imagination
. Euler and Koltanowski
, however, were not imagining they were mentally creating mathematics and playing chess – they really were.
There is a link here in the very language used: chess players talk of calculating possibilities and are sometimes asked, ‘How many moves ahead can you
calculate
?’ A player admits he made a mistake because he
calculated
wrongly although no arithmetic was involved: the player calculated through a tree of possibilities: ‘If I play Qe5, that threatens mate, Black can defend with Ne8, but then I can play h6…’ and so on. What a significant form of words! Why would anyone
calculate
the moves in a game which have nothing to do with numbers, if there were not some mysterious connection between calculating with numbers and calculating the moves of the pieces?
calculate
?’ A player admits he made a mistake because he
calculated
wrongly although no arithmetic was involved: the player calculated through a tree of possibilities: ‘If I play Qe5, that threatens mate, Black can defend with Ne8, but then I can play h6…’ and so on. What a significant form of words! Why would anyone
calculate
the moves in a game which have nothing to do with numbers, if there were not some mysterious connection between calculating with numbers and calculating the moves of the pieces?
Strong chess players can ‘look ahead’ in a position – tracing a complex tree of possible sequences of moves – in order to decide which move to make. Written
Three blind mathematiciansBlind mathematicians are rare, but they do exist and they have reached to the very top. (Are there blind theoretical physicists or chemists?) No doubt psychologists could learn much by studying how they think. Ironically, they have been as distinguished at geometry as at algebra, partly by exploiting their sense of touch.Nicholas Saunderson (1682–1739) was blinded by smallpox at the age of 12 but became Lucasian Professor of Mathematics at Cambridge University. He wrote a textbook,
Elements of Algebra
, and lectured on optics. He also invented the pin-board, much used today by primary school pupils, to create geometrical figures that he could feel with his fingers, a sort of Braille geometry.Lev Pontryagin (1908–1988) lost his sight in an accident at the age of 14. His devoted mother read books to him, wrote his notes and even learnt to read foreign languages for his sake. At 25 he entered Moscow University, blind but able to remember all his lectures. He published his first original work at the age of 19, like Euler, and went on to become one of the great mathematicians of the twentieth century.[O’Connor & Robertson 2006]Bernard Morin (1931–) has been blind since the age of 6, but became a brilliant geometer who discovered how to turn a sphere inside out – yet another ironic achievement for a mathematician who can feel but not see – and what is now called Morin's surface.
not usually
how it is thought through by the player, a very short sequence might go something like this:
‘If I play Qe4, then Black can defend by Re8, but then I play Bc3, and if he defends by Nf8 then he has no defence against Nh5, but if he plays g6 instead then I can still play Nh5 and he's helpless. So I play Qe4…’
Mathematicians may also ‘look ahead’ when examining, for example, a geometrical diagram: ‘If I draw AX parallel to BC then the triangles AXR and BYC will be similar, and so AX/BY = XR/YC. That's the right ratio but now I must link BY and YC. How can I find the ratio BY/YC?’
Chess and traditional Euclidean geometry are both highly visual, but what about algebra? Surprisingly, algebra is also highly ‘visual’. When you look at a line of algebra, you see no geometrical points and lines, no angles or areas, no surface or volume, but you do see relationships between the symbols and pattern and structure in the whole – as we shall illustrate later.
Chess pieces (or Go stones, or playing cards) are very strange objects. To highlight their strangeness, let's look at some sample objects, at how they exist and how we think about them:
a wooden post
will also vary somewhat from yours.) You can hit someone with a wooden post but you can't hit them with the idea of a ‘wooden post’.
the situation is reversed
. The chess king exists mentally defined solely by the
rules. ‘Out there’ we have millions of different
representations
or
realisations
of the chess king, actual pieces which are parts of chess sets and are used by actual players. Because they are only realisations of the mental concept, they are of all shapes and sizes and made from all sorts of different materials. The one crucial feature is that they are
recognised
as chess kings and this
recognition
depends entirely on convention. Today's convention in international matches and tournaments is to use pieces of Staunton design (named after the nineteenth-century English chess master) but readers of chess books and computer players are accustomed to different conventions for representing the chess pieces.
- ‘out there’
- ‘in my head’
- the British Museum
- my conception of the British Museum
- ‘out there’
- ‘in my head’
- a wooden post
- my conception of a wooden post
a wooden post
will also vary somewhat from yours.) You can hit someone with a wooden post but you can't hit them with the idea of a ‘wooden post’.
- ‘in my head’
- ‘out there’
- the chess king
- a representation of the chess king
the situation is reversed
. The chess king exists mentally defined solely by the
rules. ‘Out there’ we have millions of different
representations
or
realisations
of the chess king, actual pieces which are parts of chess sets and are used by actual players. Because they are only realisations of the mental concept, they are of all shapes and sizes and made from all sorts of different materials. The one crucial feature is that they are
recognised
as chess kings and this
recognition
depends entirely on convention. Today's convention in international matches and tournaments is to use pieces of Staunton design (named after the nineteenth-century English chess master) but readers of chess books and computer players are accustomed to different conventions for representing the chess pieces.
- ‘in my head’
- ‘out there’
- the number 17
- assorted numerals, each representing the number 17
The abstract Bridges of Königsberg
diagram is also a novel kind of object. It exists in physical form on paper, on a page of this book, but it crucially exists abstractly in my mind, though not in the same way as my mental picture of the view from the window of my workroom or my memory of a dream or my mental picture of an apple or a billiard table.
diagram is also a novel kind of object. It exists in physical form on paper, on a page of this book, but it crucially exists abstractly in my mind, though not in the same way as my mental picture of the view from the window of my workroom or my memory of a dream or my mental picture of an apple or a billiard table.
The problem with those mental ‘images’ is that I cannot communicate them to you clearly and unambiguously – yet I
can
by using very simple language communicate to you very precisely and successfully a unicursal diagram or the puzzle of the Tower of Hanoi
. So we can say that my mental representation of the number 17 or of the Tower of Hanoi puzzle is not
mental and private
but
mental and (potentially) public
.
can
by using very simple language communicate to you very precisely and successfully a unicursal diagram or the puzzle of the Tower of Hanoi
. So we can say that my mental representation of the number 17 or of the Tower of Hanoi puzzle is not
mental and private
but
mental and (potentially) public
.
The world ‘out there’ is full of objects, studied by scientists, which were created at some particular time or evolved over time and which may someday be destroyed – and we have conceptions of many of these objects in our heads – but we also have in those wonderful brains of ours, conceptions that were not created in the same way and which will never vanish in the same way either, strange objects that are simultaneously extremely private and also, potentially, extremely public and incredibly widely shared.
The exceptions are people who have never learnt about them or find them difficult to learn, perhaps because it's an advanced topic in mathematics only understood by a few cognoscenti. That's why millions of players world wide share their understanding of the rules of chess and always play by those rules (occasional cheats excepted). It's also why mathematics can be so easily
A deep philosophical errorPhilosophers have long distinguished between two basic types of objects (only), universals and particulars. Particulars, such as an apple or gate post, were no problem, and neither were the ideas of an apple or the idea of a gate post since everyone could agree that my idea of an apple might be subtly different from yours.Universals, such as the number 2 were a different matter. They seemed to exist independently of individual human minds, but how was this possible? The Greek philosopher Porphyry
asked: ‘Are they beings with independent existence or do they exist only as human concepts?’The puzzle was: if the number 2 has an ‘independent existence’, then where is it? And if it does not have an existence independent of human minds, how can it be ‘the same’ in every mind? Surely the number 2 is the same for you as it is for me, and everyone else who is very basically numerate?According to the philosopher Bertrand Russell:The argument that 2 is mental requires that 2 should be essentially an existent. But in that case it would be particular, and it would be impossible for 2 to be in two minds, or in one mind at two times. Thus 2 must be in any case an entity, which will have being even if it is in no mind.No wonder that, according to Russell,mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true,or that the number 2 is,a metaphysical entity about which we can never feel sure that it exists or that we have tracked it down.Russell and other traditional philosophers have been mistaken because they have had no conception of the peculiar status of chess pieces and other game-like objects. They have never taken abstract games seriously as a subject for investigation and so have not realised that there are three fundamental kinds of objects, not two.
It seems then that there are three distinctly different kinds of objects, illustrated by these three examples:
because it was originally created
in a mind.
- dreams
- mental and private
- apples
- physical and public
- the chess king
- mental and public
because it was originally created
in a mind.
No wonder, therefore, that chess is described as an
abstract
game and mathematics as an
abstract
activity. They both deal with situations in which
all
contingent features have been abstracted, stripped away.
abstract
game and mathematics as an
abstract
activity. They both deal with situations in which
all
contingent features have been abstracted, stripped away.
Chess is still an abstract game to players who cannot visualise the board and pieces mentally. (Individuals differ greatly in their ability to visualise.) You can tell this from the fact that the board and pieces can be many different sizes and shapes and made out of more-or-less any material. What's important for the play of the game is the structure of the board and the moves of the pieces: that chess once represented a battle between two armies no longer matters. The oriental game of Go (the Japanese name: it is called Wei-ch'i in Chinese) is also supposed to be a formalisation of conflict, but of
guerilla
warfare. Scott Boorman even wrote a book,
The Protracted Game: a Wei-ch'i Interpretation of Maoist Revolutionary Strategy
, but its original meaning matters not a jot when it is stripped down to a board divided by 19 lines in each direction plus two bowls full of black and white stones.
guerilla
warfare. Scott Boorman even wrote a book,
The Protracted Game: a Wei-ch'i Interpretation of Maoist Revolutionary Strategy
, but its original meaning matters not a jot when it is stripped down to a board divided by 19 lines in each direction plus two bowls full of black and white stones.
Other books
What a Lady Needs for Christmas by Grace Burrowes
Empty Nets and Promises by Denzil Meyrick
Hearts On Fire by Childs, Penny
Deadly Is the Night by Dusty Richards
Dangerous Deception by Peg Kehret
Morning's Journey by Kim Iverson Headlee
The Fading by Christopher Ransom
The Alpha's Desire 4 by Willow Brooks
314 Book 2 by Wise, A.R.
The Sin Eater by Sarah Rayne