Games and Mathematics (2 page)
Read Games and Mathematics Online
Authors: David Wells
Acknowledgements
Part I
The illustration of the tower of Hanoi on page 17 is reproduced with permission from
Book of Curious and Interesting Puzzles
[Wells 1992/2006: 66] published by Dover publications, Inc. New York.
Book of Curious and Interesting Puzzles
[Wells 1992/2006: 66] published by Dover publications, Inc. New York.
The diagram of the 21-point cubic (page 128) is from
The Penguin Dictionary of Curious and Interesting Geometry
[Wells
1991
: 43] and is reprinted by permission of John Sharp, the illustrator of that book, who also produced the image of Fatou dust on page 212.
The Penguin Dictionary of Curious and Interesting Geometry
[Wells
1991
: 43] and is reprinted by permission of John Sharp, the illustrator of that book, who also produced the image of Fatou dust on page 212.
The figure of the Al Mani knight tour (page 15) can be found at
www.mayhematics.com/t/history/1a.htm
and elsewhere.
www.mayhematics.com/t/history/1a.htm
and elsewhere.
Mathematical recreations and abstract games
Introduction
Everyday puzzles
Introduction
Abstract games,
traditional puzzles and mathematics are closely related. They are often extremely old, they are easily appreciated across different cultures, unlike language and literature, and they are hardly affected by either history or geography. Thus the ancient Egypt
ian game of
Mehen
which was played on a spiral board and called after the serpent god of that name, disappeared from Egypt round about 2900–2800 BCE according to the archaeological record but reappeared in the Sudan in the 1920s. Another game which is illustrated in Egyptian tomb paintings is today called in Italian,
morra
, ‘the flashing of the fingers’ which has persisted over three thousand years without change or development. Each player shows a number of fingers while shouting his guess for the total fingers shown. It needs no equipment and it can be played anywhere but it does require, like many games, a modest ability to count [Tylor
1879
/1971: 65].
traditional puzzles and mathematics are closely related. They are often extremely old, they are easily appreciated across different cultures, unlike language and literature, and they are hardly affected by either history or geography. Thus the ancient Egypt
ian game of
Mehen
which was played on a spiral board and called after the serpent god of that name, disappeared from Egypt round about 2900–2800 BCE according to the archaeological record but reappeared in the Sudan in the 1920s. Another game which is illustrated in Egyptian tomb paintings is today called in Italian,
morra
, ‘the flashing of the fingers’ which has persisted over three thousand years without change or development. Each player shows a number of fingers while shouting his guess for the total fingers shown. It needs no equipment and it can be played anywhere but it does require, like many games, a modest ability to count [Tylor
1879
/1971: 65].
As, of course, do dice games. Dice have been unearthed at the city of Shahr-i Sokhta, an archaeological site on the banks of the Helmand river in southeastern Iran dating back to 3000 BCE and they were popular among the Greeks and Romans as well as appearing in the Bible.
The earliest puzzles or board games and those found in ‘primitive’ societies tend to be fewer and simpler than more recent creations yet we can understand and appreciate them despite the vast differences in every other aspect of culture.
‘Culture’ is undoubtedly the right word: puzzles and games are not trivia, mere pleasant pastimes which offer fun and amusement but serious features of all human societies without exception – and they lead eventually to mathematics. String figures are a perfect example. They have been found in northern America among the Inuit, among the Navajo and Kwakiutl Indians, in Africa
and Japan and among the Pacific islands and the Maori and Australian aborigines [Averkieva & Sherman
1992
]. This is not necessarily evidence of ancient exchanges between cultures. It could just be that people everywhere tend to fiddle with bits of string – and the results can be very pleasing, like the Jacob's ladder
in
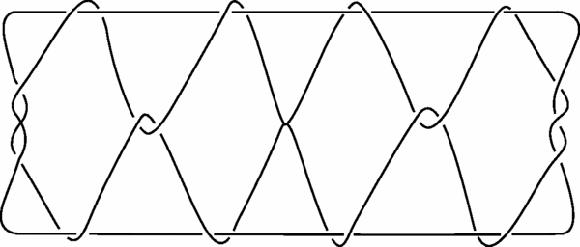
Figure 1
.
and Japan and among the Pacific islands and the Maori and Australian aborigines [Averkieva & Sherman
1992
]. This is not necessarily evidence of ancient exchanges between cultures. It could just be that people everywhere tend to fiddle with bits of string – and the results can be very pleasing, like the Jacob's ladder
in
Figure 1
.
Figure 1
Jacob's ladder
Jacob's ladder

String figures are extremely abstract. Although usually made on two hands, or sometimes the hands and feet or with four hands, Jacob's ladder would be recognisably ‘the same’ if it were fifty feet wide and made from a ship's hawser, yet these abstract playful objects can also be useful. The earliest record of a string figure is the
plinthios
(
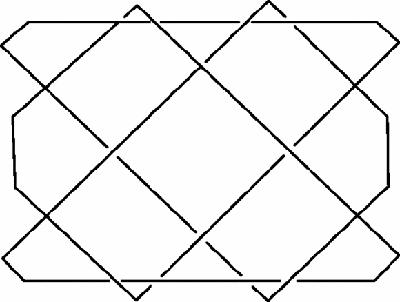
Figure 2
), described in a fourth-century Greek miscellany. It was recommended for supporting a fractured chin, and much resembles the Jacob's ladder figure [Probert
1999
].
plinthios
(
Figure 2
), described in a fourth-century Greek miscellany. It was recommended for supporting a fractured chin, and much resembles the Jacob's ladder figure [Probert
1999
].
Figure 2
Plinthios
string figure
Plinthios
string figure

No surprise then that string figures are more than an anthropological curiosity, that they are mathematically puzzling, related to everyday knots
– including braiding, knitting, crochet and lace-work – and to one of the most recent branches of mathematics, topology
.
– including braiding, knitting, crochet and lace-work – and to one of the most recent branches of mathematics, topology
.
The oldest written puzzle plausibly goes back to Ancient Egypt
:
:
There are seven houses each containing seven cats. Each cat kills seven mice and each mouse would have eaten seven ears of spelt. Each ear of spelt would have produced seven
hekats
of grain. What is the total of all these?
This curiosity, paraphrased here, is problem 79 in the Rhind papyrus
which was written about 1650 BC. Nearly 3000 years later in his
Liber Abaci
(1202), Fibonacci
posed this problem:
which was written about 1650 BC. Nearly 3000 years later in his
Liber Abaci
(1202), Fibonacci
posed this problem:
Seven old women are travelling to Rome, and each has seven mules. On each mule there are seven sacks, in each sack there are seven loaves of bread, in each loaf there are seven knives, and each knife has seven sheaths. The question is to find the total of all of them.
It is tempting to suppose that these puzzles are related. If they are, could there be a historical connection across 5000 years with this riddle from the British eighteenth century Mother Goose collection?
As I was going to St. Ives,I met a man with seven wives.Each wife had seven sacks,Each sack had seven cats,Each cat had seven kits;Kits, cats, sacks and wives,How many were going to St. Ives?
Another widespread puzzle concerns a man, a wolf, a goat and a cabbage, to be transported across a river in a small boat, never leaving the wolf alone with the goat or the goat alone with the cabbage. It first appeared in a collection attributed to the medieval scholar Alcuin of York (735–804),
Propositions to Sharpen the Young
[Alcuin of York
1992
].
Propositions to Sharpen the Young
[Alcuin of York
1992
].
Tartaglia (1500–1557) who famously solved the cubic equation and then gave the solution to Cardan who scandalously broke his solemn agreement not to publish it, printed a version featuring three brides and their jealous husbands who have to cross a river in a boat that will only take two people. If no bride can be accompanied by another women's future husband, how many trips are required?
Essentially the same puzzle is also found in Africa, in Ethiopia, in the Cape Verde Islands, in Cameroon, and among the Kpelle of Liberia and elsewhere. Since these African versions are often logically distinct from the Western, they may well be entirely independent: the difficulty of transporting uncongenial items across a river used to be universal [Ascher
1990
].
Another traditional puzzle appeals to me because it sets the solver a trap, albeit a rather obvious one. Here is one version. A snail – or a serpent or a frog! – lies at the bottom of a well, 30 units deep. It climbs 6 units every day but falls back 3 units every night. How long does it take to escape from the well? The obvious answer is that the snail rises 3 units every day-and-night, on balance, so it takes 10 days-and-nights to escape, but this is wrong because it will actually reach the top of the well half-way through the 10th day and after only 9 nights.
1990
].
Mathematics and riddles‘Mathematics has much in common with riddling, and with humour. Everything in mathematics has many meanings. Every diagram and every figure, every sum and every equation, can be “seen” in different ways. Every sentence, in English or in algebra, can be variously read and interpreted.…Mathematics, riddles and, humor have something else in common. They share similar emotions. Humor, of course, is quick. No one laughs at a joke which has taken an hour to work out, and a joke that has to be explained is an embarrassment to the comedian and the audience. Riddles are harder work. Mathematics – and science – are harder still, but even more enjoyable.…This book is about solving mathematical riddles by “seeing”, sometimes with the eyes, sometimes without.’Here are four mathematical puzzles expressed in the form of traditional riddles to illustrate the connection:‘A cube is to an octahedron as a tetrahedron is to…?‘I am 20 less than my square. What number am I?’‘What is the difference between the square of a cube and the cube of a square?’‘I have 4 sides but only a single line of symmetry. My brother has the same property but he and I are different. What are we?’
This amuses me and must have amused many many people in the past because the puzzle is first found in the Indian Bakhshali manuscipt from the 7th century CE and appears again during the Renaissance in puzzle collections by Dell’Abaco in about 1370 and then by Chuquet in 1484 and in many collections since.
Many everyday
situations easily give rise to puzzles. Take a situation, spot a formal feature, strip away everything else and you may have a puzzle which will provide amusement, recreation and fun. The Romans punished companies of soldiers who were cowardly in battle by decimation. They were lined up and every tenth man was executed. Here is a puzzle on the same principle, called after the Jewish historian Josephus who is supposed to have saved himself by just such a trick as the puzzle describes:
situations easily give rise to puzzles. Take a situation, spot a formal feature, strip away everything else and you may have a puzzle which will provide amusement, recreation and fun. The Romans punished companies of soldiers who were cowardly in battle by decimation. They were lined up and every tenth man was executed. Here is a puzzle on the same principle, called after the Jewish historian Josephus who is supposed to have saved himself by just such a trick as the puzzle describes:
Josephus, during the sack of the city of Jotapata by the Emperor Vespasian, hid himself in a cellar with forty other Jews who were determined to commit suicide rather than fall into the hands of the Romans. Not wishing to abandon life, he proposed that they form a circle and that every third person, counting round the circle, should die, in the order in which they were selected. In other words, the count was: ‘one, two three, out, four five six, out, seven…’ Where did he place himself, and a companion who also wished to live, in order to ensure that they were the last two remaining?
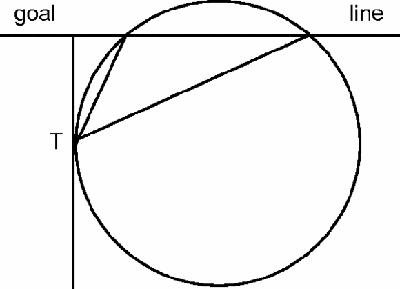
Anyone might notice that standing right under a statue on a plinth does not give the best view, but nor does standing far away. Here is the resulting puzzle: from which point does the statue
subtend
the greatest angle? This puzzle has been re-invented many times, most recently as a problem about rugby:
subtend
the greatest angle? This puzzle has been re-invented many times, most recently as a problem about rugby:
According to the rules of rugby football, a conversion of a try must be taken on a line extending backwards from the point of touchdown, at right-angles to the goal line. From which point on this line should the conversion be taken if the aim is to maximise the angle subtended by the goal-posts?
Figure 3
Angle of rugby conversion puzzle
Angle of rugby conversion puzzle

The solution,
for the mathematician but not necessarily for the practising rugby player, is to draw a circle through the goal posts which touches the perpendicular line on which the conversion must be taken (
Figure 3
). The kick should be taken from T.
for the mathematician but not necessarily for the practising rugby player, is to draw a circle through the goal posts which touches the perpendicular line on which the conversion must be taken (
Figure 3
). The kick should be taken from T.
Russian parents used to challenge their children as young as five or six years with Merchant's Problems
, tricky questions to make them think. Here is one of them, paraphrased from the late great Russian mathematician Vladimir Arnol'd, which has subsequently become a well-known puzzle in the West:
, tricky questions to make them think. Here is one of them, paraphrased from the late great Russian mathematician Vladimir Arnol'd, which has subsequently become a well-known puzzle in the West:
From a barrel of beer you transfer one teaspoonful of beer into your teacup. Then you transfer one teaspoonful of the mixture back into the barrel of beer. Is there now more beer in the tea or more tea in the beer?
These cunning questions were not unlike some traditional riddles that survived in our society into the Victorian era, and then died out, apart from some degenerate forms which appear in children's comics. Here are some modern mathematical ‘tricky questions’, suitable for pupils:
Why is 3 times 4 equal to 4 times 3?
What is the greatest number less than 10?
Does 10 have a square root?
Can you always tell if one fraction is bigger than another?
Does every shape have an area?
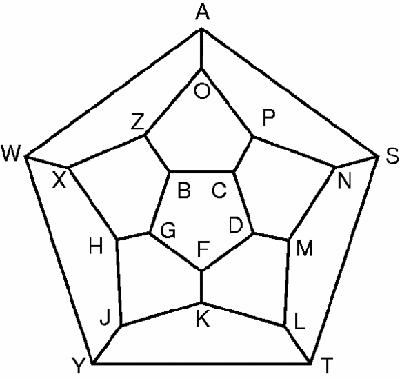
The next puzzle is more artificial. It was created by William Rowan Hamilton, a famous nineteenth-century mathematician, who sold the rights to Jacques,
Figure 4
The Icosian Game
The Icosian Game

manufacturers of fine chess sets, for the sum of £25. It was first sold in London in 1859 as a solid puzzle and later as a flat version called
The Icosian Game
.
The solid wooden puzzle was in the form of an icosahedron with the names of 20 cities marked at its vertices from B for Bruxelles to Z for Zanzibar with a few letters left out. The flat version had the design in
Figure 4
.
The Icosian Game
.
The solid wooden puzzle was in the form of an icosahedron with the names of 20 cities marked at its vertices from B for Bruxelles to Z for Zanzibar with a few letters left out. The flat version had the design in
Figure 4
.
The object of the game was to start at B and travel along the edges of the icosahedron to Z, visiting every city once and only once. Graph theorists today call the solution to such a puzzle, on any graph, a
Hamiltonian circuit
.
Hamiltonian circuit
.
In all these puzzles, the element of challenge and mystery is the hook, and the child – and many an adult – is happy to be caught.
Construction toys illustrate a different type of formality. LEGO
®
, named by its Danish inventor for
leg godt
, meaning
to play well
, has been awarded the title of ‘the greatest plastic product of all time’. It is also extremely formal and mathematical, like MECCANO and other construction toys. Because the pieces are manufactured to fine tolerances they can easily be joined in innumerable different ways – there are more than 100 million different ways to combine the six eight-stud bricks of the same colour.
®
, named by its Danish inventor for
leg godt
, meaning
to play well
, has been awarded the title of ‘the greatest plastic product of all time’. It is also extremely formal and mathematical, like MECCANO and other construction toys. Because the pieces are manufactured to fine tolerances they can easily be joined in innumerable different ways – there are more than 100 million different ways to combine the six eight-stud bricks of the same colour.
In the child's imagination the pieces always fit perfectly, of course: it is only in real life that this perfect game-like-ness sometimes breaks down. If we think of LEGO-in-the-mind as a construction game in which every move can be made perfectly, then real LEGO
®
with real coloured plastic pieces is a very precise but not-quite-perfect model of the mental game.
®
with real coloured plastic pieces is a very precise but not-quite-perfect model of the mental game.
Continuing our gentle meander from puzzles to abstract games and on to mathematics, we come to those popular
mathematical recreations
that elegantly and intriguingly link all three themes together in a tight knot of fascination. Several of these recreations – unicursal puzzles, knight tours and the Tower of Hanoi – are presented in
Chapter 1
.
mathematical recreations
that elegantly and intriguingly link all three themes together in a tight knot of fascination. Several of these recreations – unicursal puzzles, knight tours and the Tower of Hanoi – are presented in
Chapter 1
.
What do these links tell us about mathematics? That's what this book is about. It's a serious misapprehension that mathematics is all about calculation. It isn't, it's about imagination, insight and intuition. Real mathematics can be illuminated from three different perspectives. It is much like a collection of abstract games, it is much like a science, and it is very much a matter of perception, of
seeing
.
seeing
.
As a collection of related games, often still changing and evolving, it has both sharp tactics and subtle strategies, standard sequences, powerful methods, familiar manoeuvres, winning ‘moves’ and brilliant combinations, all within the
miniature world
of the game as created by the rules. It is because mathematics is game-like that mathematicians can
prove
their conclusions. However, they also
ask questions about
the game. Often this leads to new ideas, to new possibilities, so the original game is transformed into something else.
miniature world
of the game as created by the rules. It is because mathematics is game-like that mathematicians can
prove
their conclusions. However, they also
ask questions about
the game. Often this leads to new ideas, to new possibilities, so the original game is transformed into something else.
As scientists, mathematicians explore their miniature worlds, observe, generalise, create hypotheses and conjectures, perform experiments to test their
speculations and draw conclusions – though as long as they are wearing their scientific hats they can never actually prove anything.
speculations and draw conclusions – though as long as they are wearing their scientific hats they can never actually prove anything.
As observers, they spot patterns and connections, observe analogies, notice unusual sequences of moves, see one situation in different ways or different situations in the same way, and generalise their results, leading to ideas of structure.
The three aspects cannot be separated. The mathematician as game-player observes and makes conjectures; the mathematician as scientist makes moves and spots possibilities; the mathematician as observer studies objects which are much like the pieces in an abstract game of chess. This book introduces all three aspects.
It is divided into two parts. Part I is about puzzles and games and mathematical recreations. Part II presents mathematics in its three aspects, naturally matching the arguments of Part I, but now illustrated by purely mathematical examples.
The final chapter takes a step back to look at society and culture as a whole and to see what game-like features we can find in it – both illuminating the role of mathematics and helping to explain why maths exists at all.
Other books
The Field of Blood by Denise Mina
For His Keeping (For His Pleasure, Book 3) by Kelly Favor
By the Horns by Rachael Slate
shift happens 03 - no were to run by peterman, robyn
El caballero del jabalí blanco by José Javier Esparza
Southern Belle's Special Gift by Marsha Hubler
The Crucifix Killer by Chris Carter
The Round House by Louise Erdrich
The Seventh Suitor by Laura Matthews