Games and Mathematics (30 page)
Read Games and Mathematics Online
Authors: David Wells
Extremal problems
Pappus
and the honeycomb
Heron's problem and all its descendants are
extremal
problems: find the greatest or the least distance, time, area, volume, action…The first person on record to tackle an extremal problem was Queen Dido of Carthage. According to Virgil's
Aeneid
, she arrived by ship on the coast of north Africa as a refugee and asked the native inhabitants for as much land as could be surrounded by a bull's hide. They agreed and she cut it into fine strips, tied them together and surrounded a local hill. Had she been a mathematician she could have enclosed a larger area by constructing a semicircle with the sea as one side, if you accept that a circle surrounds the greatest area possible for its circumference (
Figure 15.9
).
extremal
problems: find the greatest or the least distance, time, area, volume, action…The first person on record to tackle an extremal problem was Queen Dido of Carthage. According to Virgil's
Aeneid
, she arrived by ship on the coast of north Africa as a refugee and asked the native inhabitants for as much land as could be surrounded by a bull's hide. They agreed and she cut it into fine strips, tied them together and surrounded a local hill. Had she been a mathematician she could have enclosed a larger area by constructing a semicircle with the sea as one side, if you accept that a circle surrounds the greatest area possible for its circumference (
Figure 15.9
).
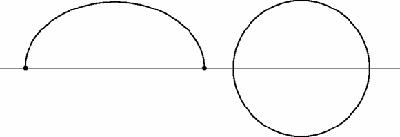
Figure 15.9
The area enclosed by a rope against a shoreline
The area enclosed by a rope against a shoreline

Suppose that Dido chose the shape on the left: we reflect it in the sea shore. The total circumference is now double the length of her hide rope, but it is not surrounding the maximum area, which would be larger if it were a circle. Therefore, she should have chosen to make a semicircle.
and the honeycomb
The Greek mathematician Pappus (290–350 CE) discussed an extremal problem that continues to delight us today:
It is of course to men that God has given the best and the most perfect notion of wisdom in general and of mathematical science in particular…to the other animals, while denying them reason, he granted that each of them should, by virtue of a certain natural instinct, obtain just so much as is needful to support life.
This instinct, says Pappus, is seen in all animals but most of all in bees. He then refers to the way they store their honey, assuming they would naturally choose a way of dividing the plane which leaves no spaces between the cells through which ‘foreign material could enter…and so defile the purity of their produce’. There are three such tessellations of regular figures, composed of equilateral triangles, squares, and regular hexagons and the bees, ‘by reason of their instinctive wisdom chose for the construction of the honeycomb the figure which has the most angles because they conceived that it would contain more honey than either of the two others’.
Their choice is therefore the regular hexagon, because as Pappus is now going on to demonstrate,
of all equilateral and equiangular plane figures having an equal perimeter, that which has the greater number of angles is always greater, and the greatest plane figure of all those which have a perimeter equal to that of the polygon is the circle.
This problem is quite unlike anything in Euclid but it is mathematical and it led in due course to a novel branch of mathematics called
the calculus of variations
after a paper by that universal mathematician, Euler. So natural history, physics and mathematics, not forgetting chemistry, have all contributed to an extraordinary symbiosis in which an attractive but strange metaphysical principle has turned out to be a goldmine of powerful theories, concepts and methods. An enigma indeed.
the calculus of variations
after a paper by that universal mathematician, Euler. So natural history, physics and mathematics, not forgetting chemistry, have all contributed to an extraordinary symbiosis in which an attractive but strange metaphysical principle has turned out to be a goldmine of powerful theories, concepts and methods. An enigma indeed.
16
The foundations: perception, imagination, insight
Chinese proofs by dissection

The foundations: perception, imagination, insight
Perception is a puzzle. We think of
visual
perception because we use our eyes so much though we perceive through all our senses. But we also say, ‘Can you see the next move?’ or ‘Can you spot the next move?’ which often means ‘Can you work it out?’ We also ask, ‘Do you see what I mean?’ which happens to be the commonest use of ‘see’ in the English language – and it's not about seeing, but about understanding!
visual
perception because we use our eyes so much though we perceive through all our senses. But we also say, ‘Can you see the next move?’ or ‘Can you spot the next move?’ which often means ‘Can you work it out?’ We also ask, ‘Do you see what I mean?’ which happens to be the commonest use of ‘see’ in the English language – and it's not about seeing, but about understanding!
Psychologists tell us that perception is an
active
and neurologically complex process. We see nothing
instantly
, only in real time. As we look at a geometrical diagram our eyes pick out particular features that are already there on the paper (or the computer screen) but we may also ‘see’ lines or circles or points that are
not yet
there. They are potential – we could add them if we chose to do so. The Greeks were keen on such constructions and often used them in their proofs. Indeed, many proofs would be impossible without them.
active
and neurologically complex process. We see nothing
instantly
, only in real time. As we look at a geometrical diagram our eyes pick out particular features that are already there on the paper (or the computer screen) but we may also ‘see’ lines or circles or points that are
not yet
there. They are potential – we could add them if we chose to do so. The Greeks were keen on such constructions and often used them in their proofs. Indeed, many proofs would be impossible without them.
So we see what is actually there, and we ‘see’ or imagine what might be, emphasising how
active
mathematics is. Indeed, we can sometimes ‘see’ what would happen if the parts of the diagram started
moving around
. We see, in our mind's eye, the effect of a
transformation
. Computer graphics can create this movement for you but this can be dangerous: a machine which replaces your brain may stop your brain working, a disaster because maths is an imaginative activity that needs an active brain.
active
mathematics is. Indeed, we can sometimes ‘see’ what would happen if the parts of the diagram started
moving around
. We see, in our mind's eye, the effect of a
transformation
. Computer graphics can create this movement for you but this can be dangerous: a machine which replaces your brain may stop your brain working, a disaster because maths is an imaginative activity that needs an active brain.
Strangely, very much the same processes occur when you look at an algebraic equation. Equations don't look like a picture and you wouldn't frame one and hang it on your wall (that is not quite true – you can purchase beautifully printed mathematical and scientific equations over the Internet) but you do scan it to pick out features, to make sense of it. In looking at this series,
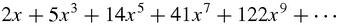
you might notice, in no particular order, that the variable is always
x
, that it contains only odd powers of
x
, and that the coefficients are rising rapidly. Look harder, and you might ‘see’ that the differences between the coefficients seem to be the rising powers of 3: 3, 9, 27…and so on.
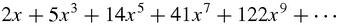
x
, that it contains only odd powers of
x
, and that the coefficients are rising rapidly. Look harder, and you might ‘see’ that the differences between the coefficients seem to be the rising powers of 3: 3, 9, 27…and so on.
You might also ‘see’ possible transformations of the equation. As always, this takes imagination. As in a chess position, there are many possible ‘moves’ and it is often not obvious which one is best. Here's an example. This quadratic equation can be transformed by dividing throughout by
x
:
 Fair enough, but what's the point? What does it
Fair enough, but what's the point? What does it
mean
? Well, it means that now you have two numbers,
x
and 15/
x
, whose product is 15, and whose sum is 8. So the original quadratic seems to be equivalent to the problem: find
a
and
b
if,
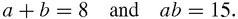 Because in this case the two numbers are integers, it is easy to spot that they are 3 and 5. This particular transformation turns out to be useful, but many aren't. There is an element of experiment. You make a move (mentally in simpler cases) to see what you get and sometimes, naturally, the experiment fails.
Because in this case the two numbers are integers, it is easy to spot that they are 3 and 5. This particular transformation turns out to be useful, but many aren't. There is an element of experiment. You make a move (mentally in simpler cases) to see what you get and sometimes, naturally, the experiment fails.
x
:

mean
? Well, it means that now you have two numbers,
x
and 15/
x
, whose product is 15, and whose sum is 8. So the original quadratic seems to be equivalent to the problem: find
a
and
b
if,
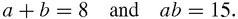
This division throughout by
x
could be a waste of time or a big step towards a general method for solving all quadratic equations. (It's the latter.) The important point is that it is entirely a matter of
algebraic
seeing. Whatever area of maths grips you, there will be
appropriate
ways of seeing and other ways which are useless, which is why Jean Dieudoneé exhorted his students to develop an
intuition for the abstract
. Since all mathematics is more-or-less abstract, his advice applies to everyone. Fortunately, there is a very enjoyable means of acquiring this intuition: just remember that – like abstract games – ‘maths is not a spectator sport’, and get stuck in!
Archimedes’ lemma and proof by lookingx
could be a waste of time or a big step towards a general method for solving all quadratic equations. (It's the latter.) The important point is that it is entirely a matter of
algebraic
seeing. Whatever area of maths grips you, there will be
appropriate
ways of seeing and other ways which are useless, which is why Jean Dieudoneé exhorted his students to develop an
intuition for the abstract
. Since all mathematics is more-or-less abstract, his advice applies to everyone. Fortunately, there is a very enjoyable means of acquiring this intuition: just remember that – like abstract games – ‘maths is not a spectator sport’, and get stuck in!
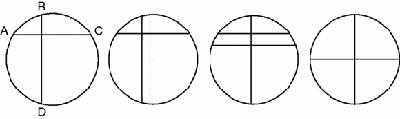
This
elegant theorem appears in a
Book of Lemmas
purportedly written by the great Greek mathematician Archimedes: two perpendicular lines divide the circumference of a circle into four arcs, AB, BC, CD and DA creating a very simple figure (
Figure 16.1
).
elegant theorem appears in a
Book of Lemmas
purportedly written by the great Greek mathematician Archimedes: two perpendicular lines divide the circumference of a circle into four arcs, AB, BC, CD and DA creating a very simple figure (
Figure 16.1
).
Figure 16.1
Archimedes’ lemma
Archimedes’ lemma

Archimedes proved that AB + CD = BC + DA. To see why this is so, move the vertical line to the right. AB increases in length by the same amount that
CD decreases so the total AB + CD does not change at all. Similarly, BC + DA is unchanged. Now move the horizontal line down a bit. The same is true.
CD decreases so the total AB + CD does not change at all. Similarly, BC + DA is unchanged. Now move the horizontal line down a bit. The same is true.
So we can move the perpendicular lines anywhere we like, provided they remain parallel to their originals, and the total lengths, AB+CD and BC + DA will remain unchanged. Fine! We choose to move them so that their intersection is the centre of the circle, then AB + CD = BC + DA = one half of the circumference and so each sum equals half the circumference.
This proof-by-transformation is typically dynamic. We
observe
how the lines
behave
when we move them. It is so convincing because it appears to depend only on the symmetry of the circle – and what could be more obvious than that?! As so often the appearance of symmetry is so overwhelming that we are once convinced [Hutchins
1952
: 564–5].
observe
how the lines
behave
when we move them. It is so convincing because it appears to depend only on the symmetry of the circle – and what could be more obvious than that?! As so often the appearance of symmetry is so overwhelming that we are once convinced [Hutchins
1952
: 564–5].
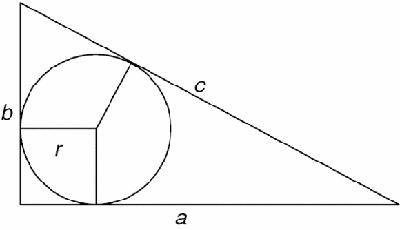
What is the radius of the incircle of the right-angled triangle in Figure
16.2
? We could calculate it by finding the area of the triangle in two ways, and comparing them.
16.2
? We could calculate it by finding the area of the triangle in two ways, and comparing them.
Figure 16.2
Chinese dissection to show inradius
Chinese dissection to show inradius

If the radius is r and the sides are
a
,
b
and
c
, then the area is equal to,
 ar
ar
+
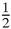 br
br
+
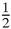 cr
cr
; but it also
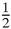 ab
ab
. Putting these two results together,
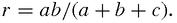
However, Liu Hui in his third-century book,
Commentary on The Nine Chapters of the Mathematical Art
, drew a diagram like Figure
16.3
(which we have simplified slightly).
a
,
b
and
c
, then the area is equal to,
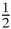 ar
ar+
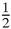 br
br+
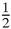 cr
cr; but it also
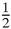 ab
ab. Putting these two results together,
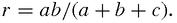
Commentary on The Nine Chapters of the Mathematical Art
, drew a diagram like Figure
16.3
(which we have simplified slightly).
Figure 16.3
Dissected triangle re-arranged
Dissected triangle re-arranged

The height of the rectangle is
r
, and its length is the distance round the triangle [Yan & Shiran
1987
: 70–71].
r
, and its length is the distance round the triangle [Yan & Shiran
1987
: 70–71].
This suggests – by analogy – that other results might be proved by dissection and indeed they were. The ancient Chinese mathematicians appreciated the value of analogy as this dialogue in the 2000-year old
Zhoubi suanjing
illustrates. Master Chen is explaining to a pupil:
Zhoubi suanjing
illustrates. Master Chen is explaining to a pupil:
The method of calculation is very simple to explain, but it is of wide application. This is because ‘man has a wisdom of analogy’ that is to say, after understanding a particular line of argument one can infer various kinds of similar reasoning, or in other words, by asking one question one can reach ten thousand things. When one can draw inferences about other cases from one instance and one is able to generalise, then one can say that one really knows how to calculate.
Master Chen continues:
after you have learnt something, beware that what you have learnt is not wide enough and after you have learnt widely, beware that you have not specialised enough.
Other books
Blessed Offense (Sixteen Seasons) by Christensen, V.R.
The Starving Years by Jordan Castillo Price
To Love Twice by McCoubrey, Heather
Defective by Sharon Boddy
White Heart by Sherry Jones
For Love of Audrey Rose by Frank De Felitta
Memories of the Heart by Marylyle Rogers
Mrs. Perfect by Jane Porter
Defy by Sara B. Larson
The Big Finish by James W. Hall