Games and Mathematics (33 page)
Read Games and Mathematics Online
Authors: David Wells
Invented or discovered? (Again)
These patterns seem to be a ‘natural’ feature of the counting numbers. We didn't put them there and nor did the ancient Greeks and if there are other intelligent beings in the universe who have developed beyond the caveman level we can be
confident that they will have thought of counting numbers and spotted features which are forced by the very process of counting in sequence, so it is tempting to say that they have been
discovered
.
confident that they will have thought of counting numbers and spotted features which are forced by the very process of counting in sequence, so it is tempting to say that they have been
discovered
.
It is true that the particular form they are given – all patterns can be represented in many ways – is at the choice of the discoverer and so we could say that, once again, there is an element of invention.
On the other hand, many different systems of counting numbers have been invented and we can be sure that any distant civilisation is sooner or later going to ‘discover’ the idea of counting and so ‘invent’ a counting system. Just as the rules of a game such as Hex or Go are invented but then force us to recognise a rich
structure of possibilities
that is not initially apparent to the players, so the very simple rules by which we count also force the existence of the rich patterns and relationships that Nichomachus started to sketch and Fermat, Euler, Gauss and many others investigated with such extraordinary imagination and insight.
structure of possibilities
that is not initially apparent to the players, so the very simple rules by which we count also force the existence of the rich patterns and relationships that Nichomachus started to sketch and Fermat, Euler, Gauss and many others investigated with such extraordinary imagination and insight.
17
Structure



Structure
Mathematics is the art of giving the same name to different things.
Mathematicians are always and everywhere looking for patterns. If they can't see patterns on the surface, they look underneath the surface. If they cannot spot a pattern in some isolated object they try to put it in a broader context.
Patterns in everyday life can be superficial – mere decoration – but in mathematics they are more significant. Rather than surface decoration, they resemble internal skeletons. They are the
structure
upon which mathematics is
constructed
and if you understand the skeleton, then you understand a lot about the object itself.
structure
upon which mathematics is
constructed
and if you understand the skeleton, then you understand a lot about the object itself.
Patterns have another use: the same patterns – or skeletons – turn up again and again in different situations, allowing insight to be spread from one to the other, so mathematicians are also, like the best scientists, obsessed with
analogies
:
analogies
:
For above all I love analogies, my most faithful teachers, acquainted with all the secrets of nature.
Spotting an analogy is just spotting a pattern or common structure so it is no surprise that analogy and structure are basic to mathematics or that beauty is so important, since beauty depends on all three features.
The next section looks at Pythagoras' theorem and at coordinates. It is a crucial feature of mathematics that a situation will be easier to understand if you
represent it appropriately
and mathematicians spend much time and effort trying to find the best representations.
represent it appropriately
and mathematicians spend much time and effort trying to find the best representations.
Following Pythagoras, we look at another aspect of structure, the search for similar structures, and for hidden structures below the surface. The primes are
very difficult to understand: one promising line of enquiry is to consider which features are peculiar to the primes alone and which features might be shared by other strange sequences – such as the lucky numbers.
very difficult to understand: one promising line of enquiry is to consider which features are peculiar to the primes alone and which features might be shared by other strange sequences – such as the lucky numbers.
If we draw graphs of quadratic functions they appear to sometimes have two roots and sometimes no roots with a ‘boundary’ case in which the parabola touches the axis. With cubic functions there are apparently 1 or 3 roots, with a similar boundary case. Look more deeply, however, and a hidden structure reveals that – when suitably viewed through the lens of complex numbers – they always have the maximum number of roots, (provided multiple roots are correctly counted), a perfect example of hidden structure illuminating the landscape.
Finally, if we understand its structure, it is often possible to transform a problem into a much easier problem, a theme that we shall illustrate by
geometrical inversion
.
Pythagoras' theoremgeometrical inversion
.
Figure 17.1
Empty space
Empty space

Figure
17.1
is a picture of some empty space. It is meant to be flat as it would be if the book were closed. Not much to look at, is there? So let's add some detail, a set of equidistant parallel lines (Figure
17.2
).
17.1
is a picture of some empty space. It is meant to be flat as it would be if the book were closed. Not much to look at, is there? So let's add some detail, a set of equidistant parallel lines (Figure
17.2
).
Figure 17.2
A sequence of equi-distant parallel lines
A sequence of equi-distant parallel lines

This is still not obviously fascinating, so in Figure
17.3
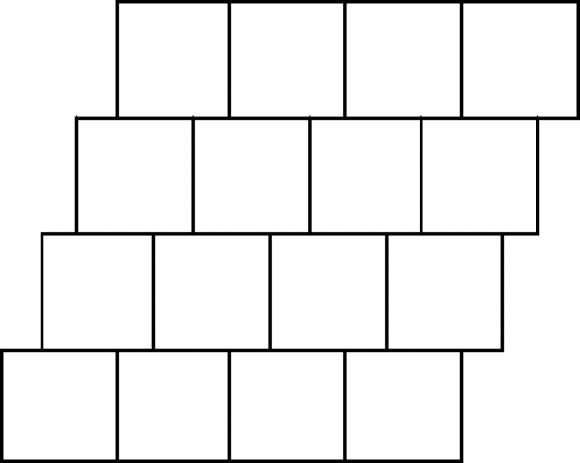
we have added a second identical set of parallel lines, perpendicular to the first, creating a grid of squares which could, in theory, continue off-page as far as we choose.
17.3
we have added a second identical set of parallel lines, perpendicular to the first, creating a grid of squares which could, in theory, continue off-page as far as we choose.
Figure 17.3
Two sets of equidistant parallel lines forming squares
Two sets of equidistant parallel lines forming squares

Squares are familiar objects, and there are many things we could do with them: what we actually do is to slide them so that each strip moves the same distance past its neighbours (Figure
17.4
).
17.4
).
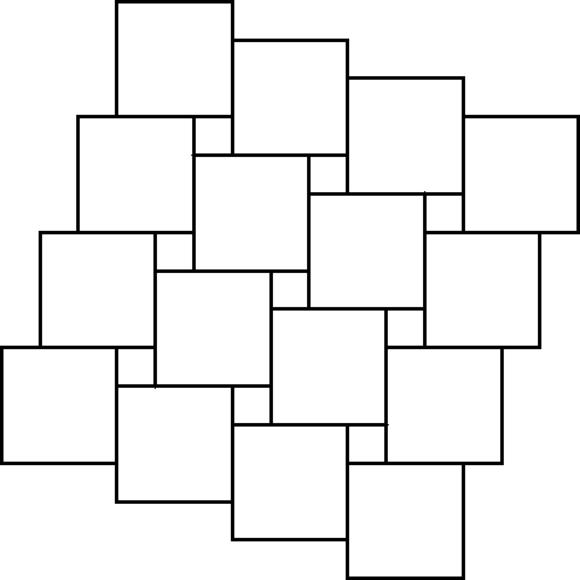
Next, we slide the squares in the perpendicular direction, by the same distance, creating a pattern full of ‘square holes’ (Figure
17.5
).
17.5
).
Figure 17.5
A pattern of square holes
A pattern of square holes

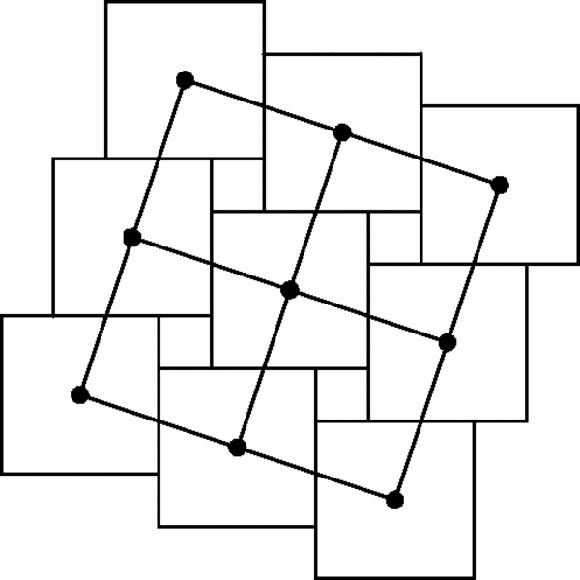
This has a simple kind of symmetry. The squares march off the edge of the diagram in two directions at right-angles which we have highlighted by choosing some suitable points, the centres of the large squares, and joining them (Figure
17.6
).
17.6
).
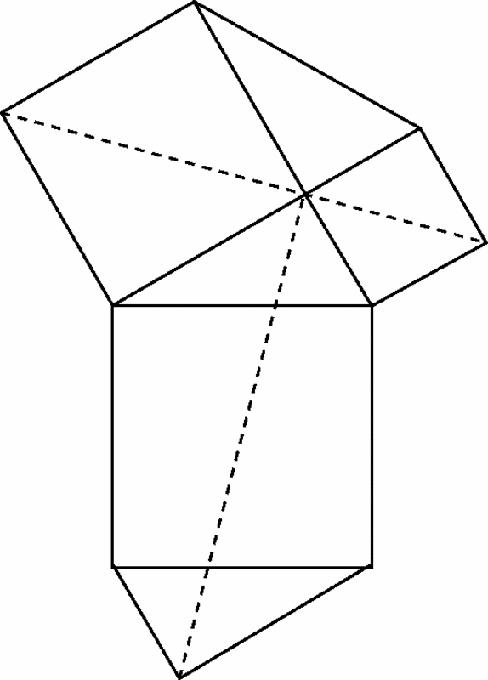
Figure 17.6
9 Offset squares with their centres joined
9 Offset squares with their centres joined

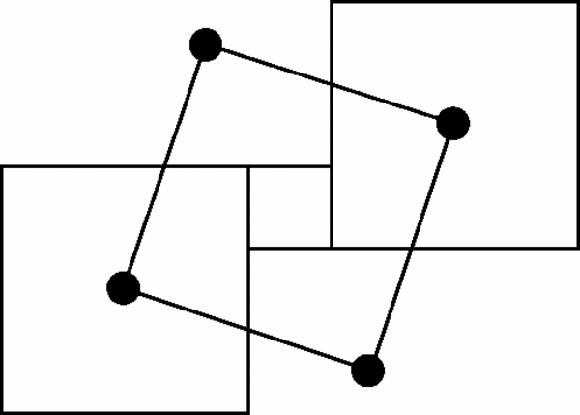
In a strange way we have got back to our first pattern of squares covering the plane, except these new squares are larger and tilted. In fact there is one large new square for each original-square-plus-square-hole. From this observation we deduce that the area of each large square
equals
the sum of the areas of a pair of smaller squares (Figure
17.7
).
equals
the sum of the areas of a pair of smaller squares (Figure
17.7
).
Figure 17.7
Part of Figure 17–6 blown up
Part of Figure 17–6 blown up

Look again, and these five pieces can be fitted together to make
either
one large square
or
two smaller squares, so we have stumbled across a dissection which proves our point.
either
one large square
or
two smaller squares, so we have stumbled across a dissection which proves our point.
We can also look at these squares in another way. If we draw the triangle in Figure
17.8
, the three sizes of squares fit round it exactly.
17.8
, the three sizes of squares fit round it exactly.
Figure 17.8
Dissection of large square into two smaller squares
Dissection of large square into two smaller squares

Aha! The theorem of Pythagoras which says that in any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares on the other two sides. By a few simple
transformations
plus, of course,
looking
we have discovered Pythagoras' theorem and a way of proving it. Or have we? On our
way we made a rather basic assumption, as often happens when you are relying on experiment and observation. We assumed that we could cover a flat plane, represented by part of the page of this book, by a set of equidistant parallel lines, but this only works for a ‘flat’ surface and not, for example, on a sphere. We can indeed divide the surface of a sphere by two set of lines, lines of longitude and latitude, but the lines of longitude are not parallel to each other (they meet at the North and South poles) and the lines of latitude are not actually
straight lines
on the sphere, because particular lines of latitude are not the shortest distances between any two points on them. (The equator is the only exception.)
transformations
plus, of course,
looking
we have discovered Pythagoras' theorem and a way of proving it. Or have we? On our
way we made a rather basic assumption, as often happens when you are relying on experiment and observation. We assumed that we could cover a flat plane, represented by part of the page of this book, by a set of equidistant parallel lines, but this only works for a ‘flat’ surface and not, for example, on a sphere. We can indeed divide the surface of a sphere by two set of lines, lines of longitude and latitude, but the lines of longitude are not parallel to each other (they meet at the North and South poles) and the lines of latitude are not actually
straight lines
on the sphere, because particular lines of latitude are not the shortest distances between any two points on them. (The equator is the only exception.)
It seems that instead of saying that on a plane surface, Pythagoras' theorem is true and we've proved it, it would be more accurate to say that
if
Pythagoras's theorem is true, all over a surface, then that surface is a plane! Instead of assuming that we know what a plane surface is – it's a kind of all-over-flat thing – we ought to admit that Pythagoras' theorem is a test for whether a surface is indeed a plane.
if
Pythagoras's theorem is true, all over a surface, then that surface is a plane! Instead of assuming that we know what a plane surface is – it's a kind of all-over-flat thing – we ought to admit that Pythagoras' theorem is a test for whether a surface is indeed a plane.
Does this mean that we can't actually prove Pythagoras? That can't be right, because it's proved in school textbooks! Indeed, but only by assuming some alternative defining properties of a plane as found in Euclid. Using such basic properties, there are many proofs, so many that Elijah S. Loomis was able to publish 367 of them in his book
The Pythagorean Proposition
(1940). Since
then many more have been discovered. Here is an old proof by Leonardo da Vinci
(Figure
17.9
).
The Pythagorean Proposition
(1940). Since
then many more have been discovered. Here is an old proof by Leonardo da Vinci
(Figure
17.9
).
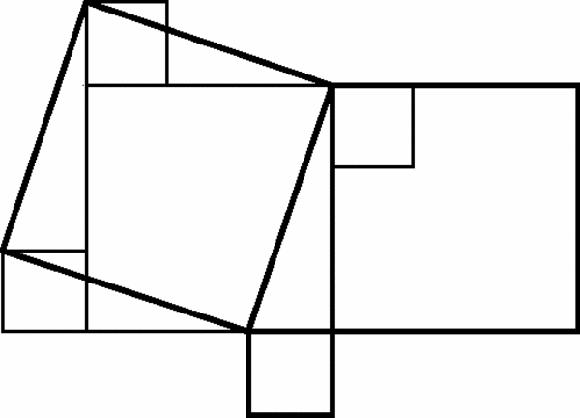
Figure 17.9
Leonardo's proof of Pythagoras
Leonardo's proof of Pythagoras

Leonardo takes a standard figure, repeats the original triangle at the bottom, and joins the two top vertices to make a third copy of the original triangle. He then draws the two thin lines, which are perpendicular, creating four identical quadrilaterals: one pair makes two original triangles and the large square; the other makes two original triangles and the two smaller squares.
But how illuminating is this proof? Drawing the two dotted lines looks like a trick which makes Pythagoras's theorem looks like a trick too, an idiosyncratic result that has no deeper significance. How misleading! The existence of hundreds of proofs of Pythagoras is rather a sign that it is very deep, though we can guarantee that few of them will explain why. They convince, but they do not illuminate.
Some proofs confirm what we suspected, but do not show why in any deeper sense, because the question, ‘Why?’ is ambiguous. Are we asking for a logically convincing proof or an illuminating proof that highlights the structure of the situation? Many proofs are the former, the best proofs are both, and some arguments are illuminating but not entirely convincing so you look for ways to tighten them up.
The artist John Constable wrote that, ‘We see nothing till we truly understand it.’ When you understand Pythagoras as a representing the
deep structure
of the geometrical plane, the diagram
looks
different and the theorem itself appears entirely obvious.
deep structure
of the geometrical plane, the diagram
looks
different and the theorem itself appears entirely obvious.
Other books
Elisabeth Crabtree - Pink Flamingo Hotel 01 - Death by Pink Flamingo by Elisabeth Crabtree
The Lincoln Conspiracy by Timothy L. O'Brien
1,001 Best Hot and Spicy Recipes by Dave Dewitt
Zodiac by Romina Russell
Ashes of the Realm: Book 04 - The Return of the Realm by Saxon Andrew
Thornlost (Book 3) by Melanie Rawn
Sam Harlan (Book 3): Damned Cold by Swaim, Kevin Lee
Wedding at Willow Lake by Mary Manners
The Gambler by Lily Graison
Under the Boardwalk by Barbara Cool Lee