Games and Mathematics (15 page)
Read Games and Mathematics Online
Authors: David Wells
8
New concepts and new objects
Does it exist?
The force of circumstance
New concepts and new objects
Mathematical explorers continually discover and name new objects in the mathematical landscape, and their features. Here are just some nouns and adjectives – there are plenty of mathematical verbs also – from the hundreds in any mathematical dictionary.
Abelian group, abundant number, affine space, area, automorphism, axis, binomial coefficient, braid, Cantor set, cardinal, Cauchy sequence, characteristic, Chinese remainder theorem, closed interval, combination, complex integration, continued fraction, cross ratio, deltoid, Desargues’ theorem, discriminant, duality, eccentricity, equation, equivalence, Euclidean, evolute, extremal, factor, factorial, Fagnano's problem, field, finite, free group, function, Galois theory, Gaussian integers, golden section, the greedy algorithm, group, Hamiltonian, harmonic, height, heptagon, hypercube, identity, imaginary number, incidence matrix, index, infinitesimal, infinite series, integer, integration, invariant, inversion, isogonal, isometry, isomorphism, iteration, Jacobian, Jordan curve, Julia set, Klein bottle, knot, Kurschak tile, Latin square, lattice, linear function, locus, logarithm, magic square, Mandelbrot set, matrix, maximum, mean value theorem, median, metric space, Möbius strip, model, modular arithmetic, nephroid, node, normal, orbit, ordinate, origin, orthogonal, packing, parabola, parallel, Pascal's triangle, Peano curve, pencil, perfect number, permutation, pigeonhole principle, pole, polygon, power, prime, probability, projection, quadrilateral, quadratic, quartile, radical axis, radius, rational, reflection, ring, rotation, ruled surface, saddle, sample, scalar, set, similarity, Simpson line, sphere, square, Stirling's formula, subtraction, symmetry, tangent, Taylor series, tessellation, topological space, torus, trace, transitive, tree, triangle, unduloid, uniform, union, value, variable, vector, vertex, Viviani's theorem, volume, weighted average, word,
x
-axis, zero, zeta function, Zorn's lemma.
x
-axis, zero, zeta function, Zorn's lemma.
Some of these are, as it were, very small objects, others are large-scale features. Many of the nouns are associated with adjectives and verbs, as in any colloquial language.
We start by glancing at the problem of naming objects. We all know that there are lots of numbers, but how can we refer to them? Next, a kind of dual problem, of objects that you can talk about easily although they don't exist! In mathematics as in real life, talk is cheap. Just because we can refer to an
odd perfect number
doesn't mean it exists. However, just because mathematicians are doing mathematics and not science they can draw firm conclusions about these ‘objects’ even if it turns out in time that their existence is impossible because it would be contradictory.
odd perfect number
doesn't mean it exists. However, just because mathematicians are doing mathematics and not science they can draw firm conclusions about these ‘objects’ even if it turns out in time that their existence is impossible because it would be contradictory.
A different kind of object is constructed to fit a specific purpose – rather as a DIY enthusiast might make a special tool – but, because this is mathematics, the tool is
forced
by the situation, if only we can work out how. We realise in the long run that the concept-object ‘has to exist’ because all the evidence points inexorably to that conclusion: and when we discover it, we are rewarded by its simplicity and power.
forced
by the situation, if only we can work out how. We realise in the long run that the concept-object ‘has to exist’ because all the evidence points inexorably to that conclusion: and when we discover it, we are rewarded by its simplicity and power.
A different problem arises when we take an informal idea such as
infinity
or
tangent
, and ask how they can be made game-like. It's easy to talk about a parabola ‘going off to infinity’ but what
ought
that to mean,
precisely
? It's easy to sketch a curve – such as a parabola – and then use a ruler to draw a straight line that (roughly) touches it, but how do we make that idea precise? While on the subject of the parabola, even the everyday idea of
shape
turns out to be surprisingly ambiguous.
Creating new objectsinfinity
or
tangent
, and ask how they can be made game-like. It's easy to talk about a parabola ‘going off to infinity’ but what
ought
that to mean,
precisely
? It's easy to sketch a curve – such as a parabola – and then use a ruler to draw a straight line that (roughly) touches it, but how do we make that idea precise? While on the subject of the parabola, even the everyday idea of
shape
turns out to be surprisingly ambiguous.
Once upon a time, the very numbers we now take for granted were a novelty. The ancient Greeks had no good method of naming numbers – they used the letters of their alphabet and soon ran short of possibilities – and the Romans as we know used the letters I, V, X, L, C, D, M for a selection of numbers from 1 to 1000. It is no surprise that calculation with these numbers was tricky, which is why for all practical purposes they used an abacus instead.
The Indian-Arabic counting system, with its notation for decimal fractions added, is superior because it lets us name far larger numbers according to a simple plan. The number 1034667 stands for,
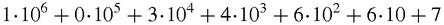
Today, mathematicians couldn't do without series based on the same idea: the variable
x
in this series appears in powers from zero upwards:
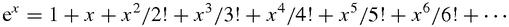However, even the Arabic system is stretched to express high numbers and so we use the notation of powers and powers of powers:
and
can be written briefly as 10
256
. This is more than merely an abbreviation – it avoids error by eliminating the need to count all those zeros. It is also greater by far than the number of particles in the universe, if cosmologists are correct, although minuscule, even negligible, when compared to numbers so large that we can hardly imagine them: infinity is a
very
long way away!
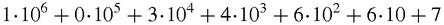
x
in this series appears in powers from zero upwards:
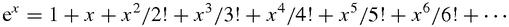
256
. This is more than merely an abbreviation – it avoids error by eliminating the need to count all those zeros. It is also greater by far than the number of particles in the universe, if cosmologists are correct, although minuscule, even negligible, when compared to numbers so large that we can hardly imagine them: infinity is a
very
long way away!
However, by
inventing
a new notation we can very easily go far beyond the customary notation for powers and powers of powers. Suppose we define 2* to mean 2
2
or 2
∧
2 and 3* to mean 3
3
3
, and so on. Conventionally, mathematicians read these ‘towers of powers’ from the top downwards so that 3* = 3
∧
(3
∧
3) = 3
27
and so on.
inventing
a new notation we can very easily go far beyond the customary notation for powers and powers of powers. Suppose we define 2* to mean 2
2
or 2
∧
2 and 3* to mean 3
3
3
, and so on. Conventionally, mathematicians read these ‘towers of powers’ from the top downwards so that 3* = 3
∧
(3
∧
3) = 3
27
and so on.
Then 2* = 4, which is very small, and 3* = 3
27
= 7625597484987, which is much larger. How large is 4*? Well, 4
∧
4 = 256, so 4
∧
(4
∧
4) = 4
256
which is approximately 1.3407796 × 10
154
or a number of 155 digits. So 4* is approximately 4
∧
(1.3407796 × 10
154
) which is a number of about 8.072297 × 10
∧
153 digits.
27
= 7625597484987, which is much larger. How large is 4*? Well, 4
∧
4 = 256, so 4
∧
(4
∧
4) = 4
256
which is approximately 1.3407796 × 10
154
or a number of 155 digits. So 4* is approximately 4
∧
(1.3407796 × 10
154
) which is a number of about 8.072297 × 10
∧
153 digits.
5* will be vastly larger again and 100* will be unimaginably large, and yet we can write it down – we have just done so – and we can also write down very briefly the fantabulously ginormous number (100*)*.
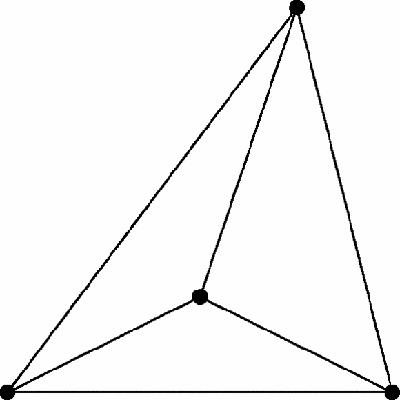
Can you draw
four equidistant points which are, let's say, 10 cm from each other? Tricky. You might start by doing what Euclid did in his
Elements
Bk.1, 1–1, and construct an equilateral triangle but when you look for a fourth equidistant point it doesn't exist – in two dimensions. However, you could add a fourth point in three dimensions, to make this regular tetrahedron (
Figure 8.1
).
four equidistant points which are, let's say, 10 cm from each other? Tricky. You might start by doing what Euclid did in his
Elements
Bk.1, 1–1, and construct an equilateral triangle but when you look for a fourth equidistant point it doesn't exist – in two dimensions. However, you could add a fourth point in three dimensions, to make this regular tetrahedron (
Figure 8.1
).
Figure 8.1
Four dots form a tetrahedron
Four dots form a tetrahedron
In other words, in two dimensions there is a contradiction in the idea of four mutually equidistant points, but in three dimensions there isn't.
Other objects are less obviously fake, for example, the
odd perfect numbers
. Perfect numbers are the sum of all their factors excluding the number itself, so 6 = 1 + 2 + 3 is the first and 28 = 14 + 7 + 4 + 2 + 1 is the second. Euclid proved in his
Elements
, Book IX, that if 2
n
− 1 is prime then 2
n
−1
(2
n
− 1) is perfect. Since 2
5
− 1 = 31 is prime, 16·31 = 496 is the third perfect number. However, Euclid's formula gives only even perfect numbers and says nothing about odd PNs. Are there any odd PNs? No one knows, but it has been proved that
if
an odd PN exists then it must be greater than 10
200
, must have at least eight prime factors and must be divisible by a prime power greater than 10
18
. And if an odd PN cannot exist? Then these statements will still be
true
– but irrelevant – curiosities.
odd perfect numbers
. Perfect numbers are the sum of all their factors excluding the number itself, so 6 = 1 + 2 + 3 is the first and 28 = 14 + 7 + 4 + 2 + 1 is the second. Euclid proved in his
Elements
, Book IX, that if 2
n
− 1 is prime then 2
n
−1
(2
n
− 1) is perfect. Since 2
5
− 1 = 31 is prime, 16·31 = 496 is the third perfect number. However, Euclid's formula gives only even perfect numbers and says nothing about odd PNs. Are there any odd PNs? No one knows, but it has been proved that
if
an odd PN exists then it must be greater than 10
200
, must have at least eight prime factors and must be divisible by a prime power greater than 10
18
. And if an odd PN cannot exist? Then these statements will still be
true
– but irrelevant – curiosities.
Mathematicians sometimes realise that an object exists but can't easily identify it or find the best, the most ‘natural’, definition. For example, it is obviously
possible to measure angles by dividing a circle into a number of parts. Usually, we use 360 parts, or degrees, for reasons that go back to the ancient Babylonians and are highly arbitrary. This is very unsatisfactory, because the standard series for sin
x
,
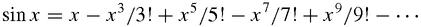and all the other usual trigonometrical series would have to be written with factors of 360 in them, if we chose any such
arbitrary
measure. To divide the circle into 100 parts would be just as arbitrary. So how
ought
angles to be measured
most naturally
?
possible to measure angles by dividing a circle into a number of parts. Usually, we use 360 parts, or degrees, for reasons that go back to the ancient Babylonians and are highly arbitrary. This is very unsatisfactory, because the standard series for sin
x
,
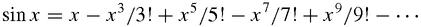
arbitrary
measure. To divide the circle into 100 parts would be just as arbitrary. So how
ought
angles to be measured
most naturally
?
Mysteriously, the answer is not to divide the circumference of the circle into any whole number of parts, but to divide it into 2π parts. The entire circumference of a unit circle is 2π by the usual formula, and so 180° becomes π, 90° becomes π/2, and so on.
(Some mathematicians seriously believe that it is an anomaly that it is 2π parts and that it should be divided into τ parts, where τ is the Greek letter
tau
, and τ = 2π or approximately 6.28. This argument will not be decided by pure logic, but by the collective judgements of many mathematicians – and the weight of history.)
tau
, and τ = 2π or approximately 6.28. This argument will not be decided by pure logic, but by the collective judgements of many mathematicians – and the weight of history.)
The new measure of angle is called the
radian
and only if we use this measure and no other will the usual series for sin
x
be so simple. Curiously, the term
radian
was first used in 1873, but the idea goes back to Roger Coates (1682–1716), and Euler who explained in his
Elements of Algebra
that angles should be measured by the length of the arc cut off on the unit circle – so although we could say that the radian was invented, it was also discovered because this simplest possible angle measure is unique and so is forced on us. The old idea of angle measure was simple but naive and it was only with advances in mathematics that the ‘true’ measure was realised.
radian
and only if we use this measure and no other will the usual series for sin
x
be so simple. Curiously, the term
radian
was first used in 1873, but the idea goes back to Roger Coates (1682–1716), and Euler who explained in his
Elements of Algebra
that angles should be measured by the length of the arc cut off on the unit circle – so although we could say that the radian was invented, it was also discovered because this simplest possible angle measure is unique and so is forced on us. The old idea of angle measure was simple but naive and it was only with advances in mathematics that the ‘true’ measure was realised.
We can say the same for everyday ideas of infinity: they may be intriguing (and attractive to poets) but they are also crude and confusing for the mathematician who needs to
formalise the informal
.
formalise the informal
.
Other books
Boys in Blue 01 - Bad Boys Bad Boys by Mia Watts
Take Her to HeVan (Nephilim Book 6) by Lucy Kelly
The Liar's Chair by Rebecca Whitney
Touch of Rogue by Mia Marlowe
Endless Love by Scott Spencer
The Seduction 3 by Roxy Sloane
The Scarlet Bride by Cheryl Ann Smith
Un anillo alrededor del Sol by Clifford D. Simak
The Spook's Apprentice by Joseph Delaney
School Reunion Year 1 by Laurel Aspen