Games and Mathematics (26 page)
Read Games and Mathematics Online
Authors: David Wells
Finally: formulae and yet more formulae
J. E. Littlewood, reviewing the collected papers of the Indian genius Ramanujan, quoted a couple of his extraordinary formulae (one is reproduced on page 213) and then remarked,
But the great day of formulae seems to be over. No one, if we are again to take the highest standpoint, seems able to discover a radically new type…[Littlewood 1986: 95]
I suppose it depends on what you mean by ‘the highest standpoint’ and ‘radically new’. Here is one of a multitude of possible counter-examples to Littlewood's pessimistic claim, created by a combination of experimental mathematics and computer power:


This result, now known as the BBP or Bailey–Borwein–Plouffe formula, has the remarkable property that by using very little computer memory and rather little calculation you can calculate the next few digits in the binary expansion of π
without calculating all the previous digits first
. So we now know that the 400 billionth binary digit of π is 0.
without calculating all the previous digits first
. So we now know that the 400 billionth binary digit of π is 0.
Just as remarkably, the formula was found not by logical reasoning but by exploiting first some clever observations and a strong sense of analogy, and then programming a computer to search for a formula for π of a certain type. The full story is told in
Experimental Mathematics: Plausible Reasoning in the 21st Century
by Jonathan Borwein and David Bailey.
Experimental Mathematics: Plausible Reasoning in the 21st Century
by Jonathan Borwein and David Bailey.
Littlewood also wrote that, referring to Ramanujan's papers,
The moral seems to be that we never expect enough; the reader…experiences perpetual shocks of delighted surprise.[Littlewood 1986: 96]
This could surely be said also of this formula for π and many other results from the new field of experimental mathematics!
14
Mathematics and the sciences
Scientists abstract
Mathematics anticipates science and technology
The success of mathematics in science
How do scientists use mathematics?
Methods and technique in pure and applied mathematics
Mathematics and the sciences
As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.
When Galileo
did his famous experiment of rolling a marble down a straight chute and timing its descent, he abstracted away the friction of the marble against the chute and the inevitable errors in his measurement of the time taken. When he argued that the flight of a cannonball could be analysed into a steady motion horizontally and an entirely separate accelerating motion vertically, he ignored the resistance of the air which would have had negligible effect on his marble in a chute but greatly distorts the flight of a cannonball from a perfect parabola.
did his famous experiment of rolling a marble down a straight chute and timing its descent, he abstracted away the friction of the marble against the chute and the inevitable errors in his measurement of the time taken. When he argued that the flight of a cannonball could be analysed into a steady motion horizontally and an entirely separate accelerating motion vertically, he ignored the resistance of the air which would have had negligible effect on his marble in a chute but greatly distorts the flight of a cannonball from a perfect parabola.
Galileo's experiments were concrete and physical but his conclusions, which he believed to be Laws of Nature ordained by God, were precise and mathematical. His results fit Einstein's
dictum
. The abstract model can be analysed with great confidence to make predictions – but the predictions will not fit reality perfectly. Plato
compared the use of mathematics for the study of reality to, ‘fitting a sandal to the foot’. It's a good analogy: the sandal should fit as closely as possible – if it doesn't it will be uncomfortable! – but no one mistakes one for the other [Young
1928
: 204].
dictum
. The abstract model can be analysed with great confidence to make predictions – but the predictions will not fit reality perfectly. Plato
compared the use of mathematics for the study of reality to, ‘fitting a sandal to the foot’. It's a good analogy: the sandal should fit as closely as possible – if it doesn't it will be uncomfortable! – but no one mistakes one for the other [Young
1928
: 204].
The ancient Greeks’ study of the conic sections as slices of circular cones is surely strange. Making a model of a cone is not easy with limited materials
and anyway why should anyone think of slicing one? We do not know – perhaps someone spotted that an asymmetrical slice was itself symmetrical and couldn't resist investigating further – but anyway, the results were beautiful and astonishing and surely very difficult, not least because you have to think in three dimensions.
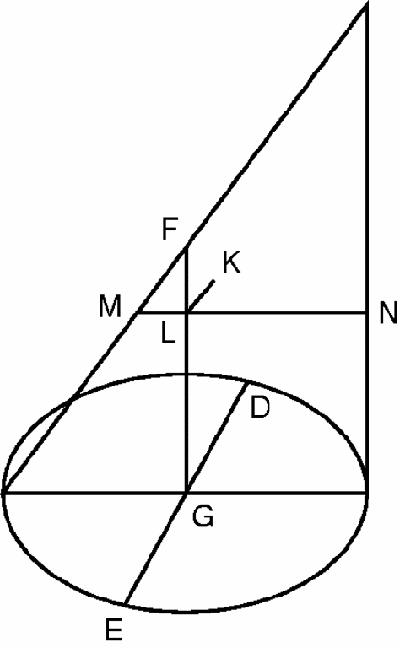
Figure 14.1
(somewhat simplified) is from Book 1, Proposition 11 of the
Conics
of Apollonius of Perga (262–190 BCE) ‘the Great Geometer’.
and anyway why should anyone think of slicing one? We do not know – perhaps someone spotted that an asymmetrical slice was itself symmetrical and couldn't resist investigating further – but anyway, the results were beautiful and astonishing and surely very difficult, not least because you have to think in three dimensions.
Figure 14.1
(somewhat simplified) is from Book 1, Proposition 11 of the
Conics
of Apollonius of Perga (262–190 BCE) ‘the Great Geometer’.
Figure 14.1
Apollonius figure
Apollonius figure

The figure shows a circular cone and a slice through E, F, K and D which is parallel to the edge through N, creating a parabola. FG is the axis of this parabola and L, a point on the axis is the mid-point of the chord through L and K. MN is the perpendicular to both LK and FG, cutting the cone at M and N.
This figure is very far from being the most complex in the work of Apollonius who often argues about plane conics by going back to their definitions as slices of cones and arguing in three dimensions: result, brilliant
pure
mathematics.
pure
mathematics.
In this figure, Apollonius proves that, in our notation, KL
2
= ML·LN. Very elegant, but what have such properties to do with science? Many centuries later, Kepler (1571–1630) was trying to use the voluminous data collected by Tycho Brahe to work out the orbits of the planets as they revolved (according to Copernicus) round the sun. He knew about the conics because Apollonius had been translated into Latin in 1536. Kepler concluded from his analysis of Brahe's data that the orbits were ellipses, and proposed his three laws of motion. Newton, whose friend Edmund Halley had published an edition of Apollonius in 1710, also studied the Greek geometer and used the geometry of the conics in his
Principia Mathematica
.
2
= ML·LN. Very elegant, but what have such properties to do with science? Many centuries later, Kepler (1571–1630) was trying to use the voluminous data collected by Tycho Brahe to work out the orbits of the planets as they revolved (according to Copernicus) round the sun. He knew about the conics because Apollonius had been translated into Latin in 1536. Kepler concluded from his analysis of Brahe's data that the orbits were ellipses, and proposed his three laws of motion. Newton, whose friend Edmund Halley had published an edition of Apollonius in 1710, also studied the Greek geometer and used the geometry of the conics in his
Principia Mathematica
.
If the Greeks had ignored sliced cones, Kepler might have merely thought that his orbits were squashed circles – and modern astronomy would have been stuck on its launching pad.
The modern hard sciences, starting with physics and astronomy, have long been highly mathematical which suggests that the world itself is essentially mathematical also. ‘God ever geometrises’ as Plato
put it. But why? Why is maths successful in the hard sciences, but not in the relatively feeble soft sciences? Here is Einstein in 1921:
put it. But why? Why is maths successful in the hard sciences, but not in the relatively feeble soft sciences? Here is Einstein in 1921:
At this point an enigma presents itself, which in all ages has agitated inquiring minds. How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality? Is human reason, then, without experience, merely by taking thought, able to fathom the properties of real things?
The success of mathematics in science reflects analogies in the physical world that are totally unexpected: for example, between the ellipses which are slices of cones or cylinders but which are also the paths of the planets, to a good approximation. This analogy was present
within
the physical world before it was analysed by mathematics. If the paths of the planets were easier to observe, more primitive men might have spotted that the curved slice of a cylindrical pole and the path of a planet appeared to be the same shape, without recognising that shape as mathematical. Why do such physical analogies exist – and why are they so precise?
within
the physical world before it was analysed by mathematics. If the paths of the planets were easier to observe, more primitive men might have spotted that the curved slice of a cylindrical pole and the path of a planet appeared to be the same shape, without recognising that shape as mathematical. Why do such physical analogies exist – and why are they so precise?
Pre-scientific men had no knowledge of the applicabilty of maths outside the business for which counting and arithmetic were invented. Of course, arithmetic works for the purposes of trade – that's why it was created – but why should the counting numbers fit very different areas of life?
Pythagoras
is a paradigm case. He discovered that the strings of musical instruments which produced certain harmonious notes when plucked had lengths in simple ratios. This seems both mysterious and apparently pointless: you don't need to understand mathematics to play a musical instrument
and most musicians are not mathematicians. Nobel prize-winning physicist Eugene Wigner once gave a much-anthologised address on ‘The unreasonable effectiveness of mathematics in the natural sciences’. He claimed that,
is a paradigm case. He discovered that the strings of musical instruments which produced certain harmonious notes when plucked had lengths in simple ratios. This seems both mysterious and apparently pointless: you don't need to understand mathematics to play a musical instrument
and most musicians are not mathematicians. Nobel prize-winning physicist Eugene Wigner once gave a much-anthologised address on ‘The unreasonable effectiveness of mathematics in the natural sciences’. He claimed that,
the enormous usefulness of mathematics in the physical sciences is something bordering on the mysterious, and that there is no rational explanation for it.
and concluded that:
The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it, and hope that it will remain valid for future research, and that it will extend, for better or for worse, to our pleasure even though perhaps also to our bafflement, to wide branches of learning.
A statistician might reply that you can easily fit any number of different curves to any set of data. Indeed, you can, but they will generally be complicated and ugly, whereas ellipses are both simple and elegant. That is the puzzle – that the mathematics used by hard scientists is so astonishingly
simple
.
simple
.
Physicists and other scientists exploring the natural world are in much the same position as the mathematician inventing – or discovering? – new mathematical objects and concepts. This can be a long process in which the naive preconception that mathematicians are always precise in their thinking and always know exactly what they are talking about, is turned on its head.
Thus mathematicians found the sums of many infinite series long before they had a clear definition of ‘the sum of an infinite series’. Even more strangely, as we have seen, Euler and others explored divergent series which apparently did not have a sum at all.
Oliver Heavyside, a great pioneer of electrical theory, was as daring and devil-may-care as most mathematicians were careful and cautious. Divergent series were just one of the novel methods that he used with great success in his work. The reaction of pure mathematicians and even other physicists was mixed. H. T. H. Piaggio, the author of a very popular textbook on differential equations, exclaimed that,
Heavyside's methods seemed a kind of mathematical blasphemy, a wilful sinning against the light. Yet Heavyside's results were always correct! Could a tree be really corrupt if it always brought forth good fruit?
On the other hand, one of his papers was rejected by the
Proceedings of the Royal Society
, an almost unheard of insult: members were generally allowed to published whatever they submitted in the
Proceedings
, but Heavyside had used divergent series rather too freely [Nahin
1988
/2002: 222–3].
Proceedings of the Royal Society
, an almost unheard of insult: members were generally allowed to published whatever they submitted in the
Proceedings
, but Heavyside had used divergent series rather too freely [Nahin
1988
/2002: 222–3].
Heavyside claimed that ‘rigorous mathematics is narrow, physical mathematics bold and broad’, and that,
In working out physical problems there should be, in the first place, no pretence of rigorous formalism. The physics will guide the physicist along somehow to useful and important results, by the constant union of physical and geometrical or analytical ideas. The practice of eliminating the physics by reducing a problem to a purely mathematical exercise should be avoided as much as possible. The physics should be carried right through, to give life and reality to the problem, and to obtain the great assistance which physics gives to mathematics.
This forceful statement both explains how Heavyside was so often correct despite his ‘dubious’ methods – he was kept on the straight and narrow by his powerful intuition – and why many pure mathematicians have no talent for applied mathematics, and vice versa. Heavyside shows a mental cast of mind which Atiyah no doubt would appreciate, but perhaps not MacLane.
The Indian-Arabic system of numerals in which we count in powers of 10, lends itself to simple sums or algorithms for the basic processes of addition, subtraction, multiplication and division and even – if you were a Victorian schoolboy – for the extraction of square and cube roots. These sums are indeed so very simple that certain seventeenth-century mathematicians decided that they could completely automate them, starting with the almost forgotten Wilhelm Schickard who built his Calculating Clock in 1623, then on through Pascal's adding machine and Leibniz's machine which did all the four basic operations. Leibniz was inspired by the thought that,
It is unworthy of excellent men to lose hours like slaves in the labour of calculation which would safely be relegated to anyone else if machines were used.[Leibniz 1685]
Today we have electronic calculators for a variety of ‘elementary’ calculations, but applied mathematicians still require methods and techniques to solve problems which cannot be solved by algorithms and yet which do not require great imagination or originality either.
This is where
mathematical methods
come into their own. When I was at college we had a giant textbook called
Methods of Mathematical Physics
by Harold Jeffreys and Bertha S. Jeffreys, both distinguished mathematicians. Today there is a plethora of books like
Mathematical Methods for Science Students
[Stephenson
1961
] which consists of 21 chapters on infinite series and calculus, differential and integral, plus 6 chapters on real numbers, inequalities, determinants, matrices, groups and vectors. All the chapters consist of extremely highly developed mathematics in which all doubts and uncertainties and ambiguities have been removed to leave the tools which science students and indeed anyone else, can use with confidence.
mathematical methods
come into their own. When I was at college we had a giant textbook called
Methods of Mathematical Physics
by Harold Jeffreys and Bertha S. Jeffreys, both distinguished mathematicians. Today there is a plethora of books like
Mathematical Methods for Science Students
[Stephenson
1961
] which consists of 21 chapters on infinite series and calculus, differential and integral, plus 6 chapters on real numbers, inequalities, determinants, matrices, groups and vectors. All the chapters consist of extremely highly developed mathematics in which all doubts and uncertainties and ambiguities have been removed to leave the tools which science students and indeed anyone else, can use with confidence.
The subtle proofs, the delicate conditions and qualifications, the dozens, even hundreds, of papers published on curious and weird objects such as Fourier series or the elliptic integrals as mathematicians attempted to understand these strange topics better and better and replace their complexity by clarity and simplicity, are nowhere to be seen.
Each topic has been reduced more-or-less to a game in which the rules of the game are clear, the allowable moves are unambiguous and the tool-user is more-or-less guaranteed to get ‘the right answer’.
Happily, the qualifications ‘more-or-less’ are still necessary. It is not illegal to attempt to find the Laplace transform of a strange function for which the standard methods don't work – but for the functions generally met with by science students, these methods will indeed function perfectly.
This process of reducing insightful and imaginative complexity to routine method, took many years, as we can see in the subject of finding the areas under curves such as the cycloid.
Other books
The Global War on Morris by Steve Israel
Signs by Anna Martin
Facing the Music by Andrea Laurence
The Strode Venturer by Hammond Innes
[Cornick Nicola] The Last Rake in London(Bookos.org) by The Last Rake in London
Taken by Norah McClintock
Rogue Dragon by Kassanna
Foxglove Summer by Ben Aaronovitch
An Outrageous Proposal by Maureen Child
No Place Like Hell by K. S. Ferguson