Games and Mathematics (24 page)
Read Games and Mathematics Online
Authors: David Wells
A Polya conjecture and refutation
The limitations of experiment
Could Goldbach's theorem
be false? History does offer some warnings. In 1919 George Polya compared the positive integers less than or equal to
N
with an
odd
number of factors and those with an
even
number of factors, and noticed that the former are apparently
never
less numerous than the latter.
be false? History does offer some warnings. In 1919 George Polya compared the positive integers less than or equal to
N
with an
odd
number of factors and those with an
even
number of factors, and noticed that the former are apparently
never
less numerous than the latter.
Calling the number of positive integers less than or equal to
N
with an odd number of factors,
O
N
, and those with an even number of factors,
E
N
, then:
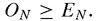 Experimental calculation showed that this conjecture was certainly true for many small numbers and it was rather assumed to be true for all numbers. Then, in 1958, it was proved that it is
Experimental calculation showed that this conjecture was certainly true for many small numbers and it was rather assumed to be true for all numbers. Then, in 1958, it was proved that it is
not
always true: there are an infinite number of exceptions. Four years later, R. S. Lehman found the first counter-example to Polya's conjecture and in 1980, M. Tanaka found the smallest counter-example, 906150257 [Haimo
1995
].
N
with an odd number of factors,
O
N
, and those with an even number of factors,
E
N
, then:
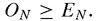
not
always true: there are an infinite number of exceptions. Four years later, R. S. Lehman found the first counter-example to Polya's conjecture and in 1980, M. Tanaka found the smallest counter-example, 906150257 [Haimo
1995
].
With the arrival of high-powered computers in recent years modern experimental mathematics has taken off, and it is even clearer that the mathematicians motto ought to be ‘caveat computat’, as the Borwein brothers
put it in presenting seven misleading equations which look as if they might be true but are in fact approximations correct to at least 30 digits and in one case to 18000 digits and in another to more than 1 billion digits [Borwein & Borwein
1992
: 622].
put it in presenting seven misleading equations which look as if they might be true but are in fact approximations correct to at least 30 digits and in one case to 18000 digits and in another to more than 1 billion digits [Borwein & Borwein
1992
: 622].
Experiment is vital to mathematics, but it has its limitations. Suppose that Cardan and later mathematicians had been content to find the roots of polynomials
by experiment. They could have found approximations to the solutions relatively easily – and we can do so almost instantly using modern computers – but if they had been content with so feeble an approach they would have missed the profound and profoundly creative ideas of complex numbers and group theory. On the other hand, if you could input the coefficients of a set of cubics into a computer program together with the solutions for each as calculated approximately, and the output was a formula linking the two sets of data then although you would initially have no idea why that formula
worked
, you would have some excellent
clues
to the deeper answer. All mathematicians are detectives and experiment can be a brilliant means of collecting clues.
by experiment. They could have found approximations to the solutions relatively easily – and we can do so almost instantly using modern computers – but if they had been content with so feeble an approach they would have missed the profound and profoundly creative ideas of complex numbers and group theory. On the other hand, if you could input the coefficients of a set of cubics into a computer program together with the solutions for each as calculated approximately, and the output was a formula linking the two sets of data then although you would initially have no idea why that formula
worked
, you would have some excellent
clues
to the deeper answer. All mathematicians are detectives and experiment can be a brilliant means of collecting clues.
Experiment has another side: possible failure. Not all experimental results are quite what they seem. Just as an apparently logically watertight proof can contain a hidden flaw, a pattern spotted in experimental data may look convincing yet actually be on further investigation, a chimaera. Here are two examples, one from number theory and the other from geometry. The first could be spotted by a bright school pupil, the second actually was.
The figure below is Pascal's triangle, also known as the binomial triangle because it appears in the coefficients of (1 +
x
)
n
.
and so on…
x
)
n
.
1 | ||||||
1 | 1 | |||||
1 | 2 | 1 | ||||
1 | 3 | 3 | 1 | |||
1 | 4 | 6 | 4 | 1 | ||
1 | 5 | 10 | 10 | 5 | 1 | |
1 | 6 | 15 | 20 | 15 | 6 | 1 |
Each number is the sum of the two numbers above it, left and right. The next figure is a variant, called the trinomial triangle because its terms appear when you expand (1 +
x
+
x
2
)
n
.
and so on…Each number is the sum of the three numbers immediately above it and to the left and right.
x
+
x
2
)
n
.
1 | ||||||||||
1 | 1 | 1 | ||||||||
1 | 2 | 3 | 2 | 1 | ||||||
1 | 3 | 6 | 7 | 6 | 3 | 1 | ||||
1 | 4 | 10 | 16 | 19 | 16 | 10 | 4 | 1 | ||
1 | 5 | 15 | 30 | 45 | 51 | 45 | 30 | 15 | 5 | 1 |
The central column, 1, 1, 3, 7, 19, 51,…is the
central trinomial sequence
t(n)
which appears in many combinatorial problems. For example,
t
(
n
)/3
n
is the probability that in a three-candidate race with
n
voters, two specified candidates will get the same number of votes.
central trinomial sequence
t(n)
which appears in many combinatorial problems. For example,
t
(
n
)/3
n
is the probability that in a three-candidate race with
n
voters, two specified candidates will get the same number of votes.
How could we predict the terms of this sequence without constructing the whole triangle?
Any school pupil with experience of trying to answer puzzles about continuing sequences will think of comparing successive terms to see how rapidly they are increasing. In this case, each term is a bit less than 3 times the previous term so we calculate 3
t
(
n
) −
t
(
n
+ 1) and see what the differences look like:
 Bingo! If we ignore for the time being the annoying first two terms, then the sequence 2, 6, 12, 30, 72…is made up of simple ‘round’ numbers which can be factorised as in the next row as products of pairs of consecutive integers. What's more, the first numbers in each pair of factors make the sequence of Fibonacci numbers, F(
Bingo! If we ignore for the time being the annoying first two terms, then the sequence 2, 6, 12, 30, 72…is made up of simple ‘round’ numbers which can be factorised as in the next row as products of pairs of consecutive integers. What's more, the first numbers in each pair of factors make the sequence of Fibonacci numbers, F(
n
) in which each number is the sum of the previous two:
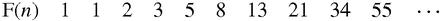 This pattern looks very convincing, going on for seven terms, but just to check it we calculate a bit farther:
This pattern looks very convincing, going on for seven terms, but just to check it we calculate a bit farther:
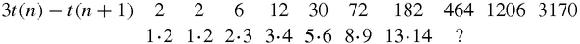 And now we see that the pattern fails because 21·22 = 462 and not 464. Similarly, 1206 is a miss: 34·35 = 1190, rather than 1206.
And now we see that the pattern fails because 21·22 = 462 and not 464. Similarly, 1206 is a miss: 34·35 = 1190, rather than 1206.
t
(
n
) −
t
(
n
+ 1) and see what the differences look like:

n
) in which each number is the sum of the previous two:
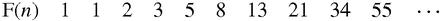
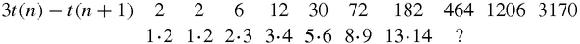
The great Euler, who was a genius at spotting patterns of all kinds, spotted this one and its failure, and write a short paper on it,
Exemplum memorabile inducionis fallacis
, or
A Memorable Example of Fallacious Induction
[Andrews
1990
] [Villegas
2007
: 121 and 92–112] [Euler 1760b].
Exemplum memorabile inducionis fallacis
, or
A Memorable Example of Fallacious Induction
[Andrews
1990
] [Villegas
2007
: 121 and 92–112] [Euler 1760b].
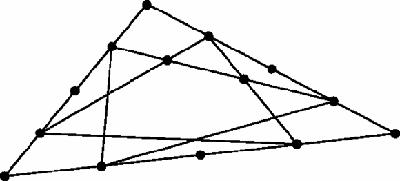
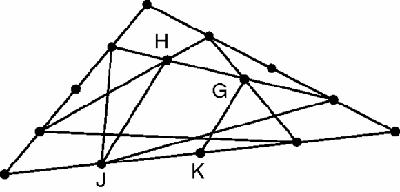
Now for a misleading geometrical figure. Daniel Schultz was 12 years old when he decided to explore a typical triangle with the quarter points marked on the sides. Joining the quarter points makes two triangles which overlap to make a hexagon (
Figures 12.1
,
12.2
).
Figures 12.1
,
12.2
).
Figure 12.1
Schultz basic figure
Schultz basic figure

Figure 12.2
Schultz figure with ‘parallel’ lines
Schultz figure with ‘parallel’ lines

Other books
The Nephilim and Pyramid of Apocalypse by Patrick Heron
Carmilla by Joseph Sheridan Le Fanu
WORTHY by Matthews, Evie
Burned: Black Cipher Files #3 (Black Cipher Files series) by Lisa Hughey
An Apple a Day Keeps the Dragon Away by Amber D Sistla
Bee Happy by Marcia C Brandt
The Eye of Elicion: The Kinowenn Chronicles Vol 1 by Rachel Ronning
Love's Last Chance by Jean C. Joachim
Five Quarters of the Orange by Joanne Harris
The Living End by Craig Schaefer