Games and Mathematics (20 page)

Read Games and Mathematics Online

Authors: David Wells

10
Mathematics becomes game-like
 
Divergent series are an example of an idea so novel and so difficult to understand that early work on divergent series was a mixture of uncertain manipulation, brilliant intuition, apparent failure, genuine errors, and incomprehensible success. It was only after many brilliant mathematicians had struggled with the idea that the dark and obscure landscape of divergent series was illuminated, and mathematicians finally decided what a divergent series ‘really is’ and how they could safely be handled.
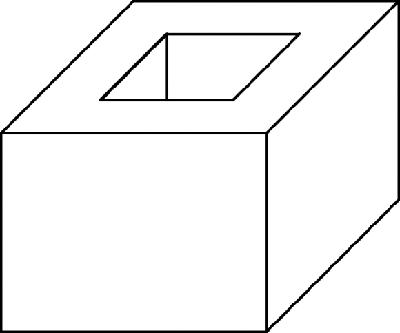
Euler's relation for polyhedra
 
A similar
confusion arose over another of Euler's interests: polyhedra. He noticed what Descartes had also seen earlier that for the simplest polyhedra, the number of vertices plus the number of faces exceeded the number of edges by 2: V + F = E + 2.
Thus, in Figure
10.1
a cube has 8 vertices, 6 faces and 12 edges, and 6 + 8 = 14 + 2. The octahedron on the right has 6 vertices, 8 faces and also 12 edges, while the irregular polyhedron below which is a square pyramid face-to-face with a cube, has 9 vertices, 9 faces and 16 edges, and 9 + 9 = 16 + 2.
 
Figure 10.1
Diagram of cube, octahedron and pyramid ON cube
 
 
Naturally
such simple observations cry out for an explanation, but all the early proofs were defective. Every proof that was offered turned out to have a destructive counter-example because no one had a clear idea of how to define a polyhedron.
Could a polyhedron have holes? Several holes? Could it consist of two parts meeting only at a point, like two pyramids joined at a common vertex? Could it be of two parts joined along an edge? What if a polyhedron intersects itself? How would you then count the edges, and faces? All the early proofs were undermined by ‘weird’ counter-examples.
If a polyhedron is defined as a solid form bounded by polygons, then the ‘doughnut’ in Figure
10.2
fits the definition. But it has 16 faces and 16 vertices but only 32 edges, so V + F = E. The hole-in-the-middle seems to have got rid of the original ‘2’.
Figure 10.2
Polyhedral doughnut
 
 
Only when the idea of what a polyhedron ‘is’ had been clarified to the satisfaction of mathematicians, was it possible to go ahead and draw conclusions about them with confidence.
This point has another side: the idea of a polyhedron was created in such a way that Euler's very simple and elegant relationship,
was true
. It turned out that the simplest and most aesthetically pleasing definition of a polyhedron fitted mathematicians’ original intuitions of what a polyhedron ‘ought to be’. Yet the process of throwing up counter-example after weird counter-example was not wasted, far from it, because it was only through being tested in the fire, as it were, that mathematicians were forced to create the ‘best’, the ‘proper’ definition – just as the best and proper definition of angle measure turned out to be the radian (p. 99).
Lakatos on
Proofs and Refutations
Imre Lakatos (1922–1974) made this example famous in his book
Proofs and Refutations
[
1976
]. This is an excellent account of the relevant history, but his conclusion, that mathematics always develops like a science, was false. He took a sequence of episodes in the history of mathematics and falsely generalised to mathematics as a whole. Most theorems go through no such historical process as he recounted.
Lakatos made the mistake of seeing mathematics as far too scientific – so that all theorems were open to potential refutation – and had no conception of mathematics as game-like.
The subtitle of
Proofs and Refutations
was
The Logic of Mathematical Discovery
. Note the definite article. He claimed that this was a ‘general method of mathematical discovery’. Criticising the deductivist style he wrote that:
 
The whole story vanishes, the successive tentative formulations of the theorem in the course of the proof-procedure are doomed to oblivion while the end result is exalted into sacred infallibility.
[Lakatos
1976
: 27]
 
Did he really believe that
all
theorems undergo ‘successive tentative formulations’? They do not. The problems he chose to analyze all involved questions of definition, that is, processes involved in the very construction of game-like mathematics, of the informal becoming formal. Of mathematics that is already adequately formalised, he said nothing at all.
In the process of formalising definitions of concepts and objects, failures of proof may be simple errors of reasoning but they may also be indications that the formalisation is itself flawed.
Vast tracts of ‘mathematical discovery’, however, do not consist of the development of such ‘informal theories’. How did Lakatos account for discovery outside his ‘informal theories’? He did not, because he had already denied them.
Lakatos seems not to have realised, or perhaps he could not accept, that if you chose to play a game – or if you invent a game yourself – certain implications
must
follow from the rules [Wells 1993b].
 
The invention-discovery of groups
 
In contrast to divergent series and polyhedra, the creators of group theory never encountered such problems. Early group theorists made many errors but – unlike the case of Euler's relation – they were game-like errors, not errors of definition.
One of the streams that led to the creation of group theory was the idea of the
permutations
of the roots of an equation. Here is an example with 5 objects which do not have to be the roots of an equation – they could be just about any objects at all.
If we start with the ordered set,
S = {a
b
c
d
e}
and they are permuted into this order
{b
c
a
e
d}
then we can see that a → b, b → c and c → a completing a cycle: a → b → c → a…At the same time, d and e just change places, d → e and e → d. We can represent the first cycle by (a b c) and the second by (d e), and the whole permutation from the 1st row to the 2nd is then clearly defined as (a b c)(d e).
Sometimes an element of a permutation does not move at all.
In this case, if
{a
b
c
d
e}
permutes into
{d
b
e
c
a}
then we can write the whole permutation as (a d c e)(b) showing that 4 letters form a cycle and b remains unchanged.
We can if we wish apply a permutation repeatedly. If we write (a b c)(d e) = X, then the results of applying X again and again are:
S =
{a b c d e}
XS =
{b c a e d}
XXS = X
2
S =
{c a b d e}
XXXS = X
3
S =
{a b c e d}
XXXXS = X
4
S =
{b c a d e}
XXXXXS = X
5
S =
{c a b e d}
XXXXXXS = X
6
S =
{a b c d e}.
So X
6
S = S. This is not a great surprise, since the permutation (b c a) when used 3 times, returns (a b c) to (a b c) and each switch (d e) ‘undoes’ the effect of the previous switch, so to ‘undo’ {b c a e d} by going forwards we must apply it 2 × 3 − 1 = 5 more times.
This is beginning, just, to look like an algebra of permutations and indeed there is a very natural way to ‘multiply’ permutations. If we write
(a b c)(d e) = X and (a d c e)(b) = Y. Then XY is defined perfectly clearly to be the effect of Y followed by the effect of X, so we have:
S =
{a b c d e}
YS =
{d b e c a}
XYS =
{e c d a b}.
If we calculate YXS by performing permutation X first and then permutation Y, the result is,
S =
{a b c d e}
XS =
{b c a e d}
YXS =
{b e d a c}.
In this case, XY does not equal YX so the permutations X and Y are
not commutative
. However, all permutations of
n
objects are
associative
, meaning that given three permutations X, Y and Z, (XY)(Z) = (X)(YZ). Also, each permutation has an
inverse
, which is the permutation which ‘undoes’ the permutation immediately.
So the inverse of,
X = (b c a)(e d)
is
X′ = (c b a)(d e)
because X′XS = S. It is also true that XX′S = S so the order of operations of X and X′ makes no difference. X and X′ do commute.
We are now close to defining a group of operations, (which does not have to be a permutation of objects). The defining rules, or axioms, of a group are that you start with a set of states and every operation leads to another state of the set. There must also be an identity operation, usually labelled I, which changes nothing. For permutations of 5 objects, the identity is the permutation I = (a)(b)(c)(d)(e). Also each operation, P has an inverse, P′ such that PP′ = P′P = I, and finally, the operations are associative.
Arthur Cayley proved that every finite group is isomorphic – meaning essentially identical to – some permutation group, so the
apparently
simple permutation groups
are actually representative of all the groups that exist. So the permutation groups are not as simple as they seem, far from it, and group theory itself is extraordinarily complex – a perfect example of how a very simple idea leads to a vast and very rich miniature world.
The point we wish to emphasise here, however, is that because of the simple and straightforward nature of the idea of a permutation, none of the difficulties and obscurities that attended the birth of a sound theory of divergent series or of polyhedra, ever appeared.
Different parts of mathematics differ greatly in their origins, and in their initial clarity or obscurity and so different mathematicians also have different views of mathematics and how it should be approached.
Atiyah and MacLane disagree
 
This argument between Saunders Maclane, author with Garrett Birkhoff of the standard textbook,
A Survey of Modern Algebra
, who recorded the incident, and Michael Atiyah, illustrates one difference very well:
 
I adopted a standard position – you must specify the subject of interest, set up the needed axioms, and define the terms of reference. Atiyah much preferred the style of the theoretical physicists. For them, when a new idea comes up, one does not pause to define it, because to do so would be a damaging constraint. Instead they talk around the idea, develop its various connections, and finally come up with a much more supple and richer notion…However I persisted in the position that as mathematicians we must know whereof we speak…This instance may serve to illustrate the point that there is now no agreement as to how to do mathematics…
[MacLane
1983
: 53]
 
Well, frankly there never was. From Archimedes to Diophantus and on to Fermat, Euler and Newton…mathematicians have succeeded with different styles and different approaches. The work of Atiyah is much more geometrical than that of MacLane's who is an algebraist. This is Atiyah's view of geometry:
 
Geometry is that part of mathematics in which visual thought is dominant whereas algebra is that part in which sequential thought is dominant. This dichotomy is perhaps better conveyed by the words “insight” versus “rigour” and both play an essential role in real mathematical problems.
[Atiyah
2003
: 29]
 
It is no accident that Atiyah turned in his later years to problems of theoretical physics. We could say that MacLane thinks of mathematics from the start as game-like – and can afford to do so because of the kind of hard-edged mathematics that he does – whereas Atiyah, as MacLane notes, is more like a physicist, who is exploring a mathematical landscape that is much less clear cut, and so he hesitates and explores further as he attempts to achieve the precision and clarity which MacLane has to begin with.
Andrew Wiles expressed very well his own sense of doing mathematics as exploring in the dark:
 
Perhaps I can best describe my experience of doing mathematics in terms of a journey through a dark unexplored mansion. You enter the first room of the mansion and it's completely dark. You stumble around bumping into furniture, but
generally you learn where each piece of furniture is. Finally, after six months or so, you find the light switch, you turn it on, and suddenly it's all illuminated. You can see exactly where you were. Then you move into the next room and spend another six months in the dark. So each of these breakthroughs, while sometimes they're momentary, sometimes over a period of a day or two, they are the culmination of – and couldn't exist without – the many months of stumbling around in the dark, that precede them.
[Griffiths
2000
]
 

Other books

Dancing with Deception by Kadi Dillon
The Sleep Room by F. R. Tallis
On Thin Ice 1 by Victoria Villeneuve
Interfictions by Delia Sherman
Eyes of Darkness by Dean Koontz
The Godwulf Manuscript by Robert B. Parker