Games and Mathematics (23 page)
Read Games and Mathematics Online
Authors: David Wells
The prime numbers
Prime pairs
The limits of conjecture
The theory of numbers, more than any other branch of pure mathematics, began by being an empirical science. Its most famous theorems have all been conjectured, sometimes a hundred years or more before they have been proved; and they have been suggested by the evidence of a mass of computation.
The prime numbers are those with no factors other than themselves and 1. The sequence starts,
It looks extremely irregular and it is. We can see why this is no surprise if we construct the Sieve of Erastosthenes, named after the brilliant astronomer and mathematician who was a friend of Archimedes
:
The sequence starts with 1 which has no factors apart from 1, but we don't actually count 1 as a prime, basically because a lot of theorems and formulae are simpler to express if you leave 1 from the list. (The Greeks thought that 1
was special, because it was the unity from which all the other counting numbers were generated so it is historically quite appropriate to make this exception.)
2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 |
41 | 43 | 47 | 53 | 59 | … |
:
(1) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
was special, because it was the unity from which all the other counting numbers were generated so it is historically quite appropriate to make this exception.)
We take the first number after 1 which is 2, and cross through all the subsequent even numbers. The first number remaining is 3, so we cross out all multiples of 3, except for 3. The next number remaining is 5, so we deleted all multiples of 5, except 5, and so on.
This seems a simple process but actually it's complicated. Let's see why. In the sequence of squares,
each square is calculated from the counting number above. It could be calculated from the previous square (you could calculate 36 from 25) but it's not quite so simple and it's not necessary. The situation with the primes is quite different. As we operate Erastosthenes’ sieve
, we only know what the next sieving number will be
at the last moment
, at the end of the previous sieving step.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | … |
, we only know what the next sieving number will be
at the last moment
, at the end of the previous sieving step.
There seems to be no simple way to calculate the
n
th prime from the number
n
, or from the (
n
−1)th prime, and indeed no such usable formula has ever been found. This is a hint that the behaviour of the primes is very irregular and that it will pose serious – but deeply fascinating! – problems. It does
not
mean that we can prove nothing about them, though the proofs of all but the simplest theorems are extremely difficult.
n
th prime from the number
n
, or from the (
n
−1)th prime, and indeed no such usable formula has ever been found. This is a hint that the behaviour of the primes is very irregular and that it will pose serious – but deeply fascinating! – problems. It does
not
mean that we can prove nothing about them, though the proofs of all but the simplest theorems are extremely difficult.
It is an obvious speculation that they go on for ever, that however far we go, we can always ‘another one’. But how might this be proved? One of Euclid
's great achievements, whether or not it was his own, was to record a simple proof that they do go ‘to infinity’. He argued that if the primes were only finite in number, for example if p were the largest:
then we could calculate the product and add 1:
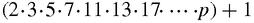 to get a number which is not divisible by any of the primes from 2 up to
to get a number which is not divisible by any of the primes from 2 up to
p
and therefore must either be prime itself or have a novel prime factor. Either way, our assumption that 2 to
p
is the set of all the primes is false.
's great achievements, whether or not it was his own, was to record a simple proof that they do go ‘to infinity’. He argued that if the primes were only finite in number, for example if p were the largest:
2 | 3 | 5 | 7 | 11 | 13 | 17 | … | … | p |
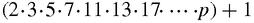
p
and therefore must either be prime itself or have a novel prime factor. Either way, our assumption that 2 to
p
is the set of all the primes is false.
Jot down the first few prime numbers, and it is impossible not to notice that some of them come in pairs:

An instant conjecture – the twin prime conjecture – is that just as there are an infinite number of primes, there is an infinite sequence of prime pairs. They may become rarer as they get larger – we would expect that too – but there will always be another one. This is believed but has not been proved.

Following the twin prime conjecture, it is natural to notice runs of primes such as 5–7–11 or 11–13–17 or 17–19–23, where the differences are always 2 then 4, and to conjecture that they also go on for ever. Easy to conjecture but difficult to prove! However, progress has been made. Many years ago, in 1923, G. H. Hardy and his long-time collaborator J. E. Littlewood published a paper containing a series of more than a dozen bold conjectures: bold, but based on their extraordinarily deep understanding of prime number theory and their own original methods. These included a formula for the expected number of twin primes; a conjecture that all prime patterns such as 5–7–11 and 5–7–11–13 and even 5–7–11–13–17 (with differences always 2, 4, 2, 4) are also infinite in number; and a formula for the number of primes of the form
n
2
+ 1 [Hardy & Littlewood
1923
: 1–170].
n
2
+ 1 [Hardy & Littlewood
1923
: 1–170].
How do you conjecture a complicated formula? As we said, Hardy and Littlewood had a profound understanding based on many years of research and many brilliant insights: on
that
kind of foundation, you can take a risk and be bold and specific. It is a mark of their profundity that not one of their conjectures has been disproved though neither have they been proved.
that
kind of foundation, you can take a risk and be bold and specific. It is a mark of their profundity that not one of their conjectures has been disproved though neither have they been proved.
The history of prime numbers
is indeed a history of experiment and conjecture as Hardy said but it doesn't follow that it could stay that way for ever. The harder the questions asked, the less reliable direct experience became. The early prime number theory of Fermat and his successors turned into, during the nineteenth century, analytic number theory, which exploited the calculus and complex variables to prove very profound theorems indeed. So G. H. Hardy, a master of the theory, issued a warning:
is indeed a history of experiment and conjecture as Hardy said but it doesn't follow that it could stay that way for ever. The harder the questions asked, the less reliable direct experience became. The early prime number theory of Fermat and his successors turned into, during the nineteenth century, analytic number theory, which exploited the calculus and complex variables to prove very profound theorems indeed. So G. H. Hardy, a master of the theory, issued a warning:
Some branches of mathematics have the pleasant characteristic that what seems plausible at first sight is generally true. In [analytic prime number] theory anyone can make plausible conjectures, and they are almost always false.
Elsewhere, Hardy pointed out that,
It is comparatively easy to make clever guesses; indeed, there are theorems, like ‘Goldbach's Theorem’, which have never been proved and which any fool could have guessed.
Goldbach (1690–1764) had conjectured in 1742 that every even number greater than 2 is the sum of two primes. The first few cases are easy to check:
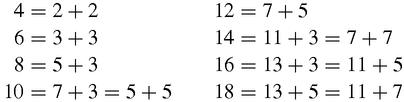 and so on. We might guess, with as little effort as Goldbach, that almost all even numbers are the sum of two primes in more than one way. Yet it is still a conjecture today, although usually referred to as Goldbach's
and so on. We might guess, with as little effort as Goldbach, that almost all even numbers are the sum of two primes in more than one way. Yet it is still a conjecture today, although usually referred to as Goldbach's
theorem
. What we do know is that every sufficiently large odd number is the sum of three primes, and that almost all even numbers are the sum of two.
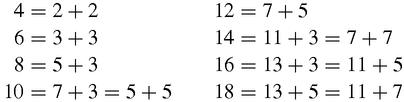
theorem
. What we do know is that every sufficiently large odd number is the sum of three primes, and that almost all even numbers are the sum of two.
Other books
Love In the Red Zone (Connecticut Kings Book 1) by Love Belvin
Los momentos y sus hombres by Erving Goffman
In the Presence of My Enemies by Gracia Burnham
Last Chance Christmas by Joanne Rock
Loved by Morgan Rice
Threads of Treason by Mary Bale
Blood of the Reich by William Dietrich
Bang The Drum Slowly by Mark Harris
Zotikas: Episode 1: Clash of Heirs by Storey, Rob, Bruno, Tom
Torpedo Run by Robb White