Games and Mathematics (38 page)
Read Games and Mathematics Online
Authors: David Wells
19
Mathematics and beauty
Experience and expectations
Beauty and Brilliancies in chess and mathematics
Beauty, analogy and structure
Mathematics and beauty
Pure mathematicians have written a stream of encomiums on the beauty of mathematics. Reading them, anyone might conclude that mathematics is an art like painting or music or poetry. The greater the mathematician, the more vividly, it seems, they appreciate its beauty. Fermat wrote to a friend, ‘I have found a great number of exceedingly beautiful theorems.’ No doubt one of the theorems he had in mind was that every prime number of the form 4
n
+ 1 is the sum of two integral squares in exactly one way. For example,
and so on. Primes of the form 4
n
+ 3, such as 7 or 19, are never the sum of two squares. This is extremely surprising, because the primes are so irregular and mysterious and the squares so regular and simple – so almost all mathematicians find his theorem extraordinarily beautiful.
n
+ 1 is the sum of two integral squares in exactly one way. For example,
n
+ 3, such as 7 or 19, are never the sum of two squares. This is extremely surprising, because the primes are so irregular and mysterious and the squares so regular and simple – so almost all mathematicians find his theorem extraordinarily beautiful.
Newton once wrote to Henry Oldenburg, the Secretary of the Royal Society in London,
I can hardly tell with what pleasure I have read the letters of those very distinguished men Leibniz and Tschirnhaus. Leibniz's method for obtaining convergent series is certainly very elegant…
We have already met Leibniz's series,
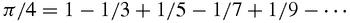What could be simpler or more elegant and, once again, surprising? Who would have thought that the ratio of the circumference of a circle to its diameter should be connected to the reciprocals of the integers?
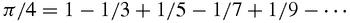
Mathematics is beautiful but mathematicians not only enjoy beauty, they use it as a criterion of success and as a guide in their work – but all guides, of course, occasionally fail. As Henri Poincaré explained,
When a sudden illumination invades the mathematician's mind…it sometimes happens…that it will not stand the test of verification…it is to be observed that almost always this false idea, if it had been correct, would have flattered our natural instincts for mathematical elegance.
Poincaré is saying that their aesthetic sense is so strong that it can even lead mathematicians astray! Note also Poincaré's reference to
verification
which, to the mathematician means
proof
. Mathematicians continually speculate but only proof certifies their conclusions.
verification
which, to the mathematician means
proof
. Mathematicians continually speculate but only proof certifies their conclusions.
How can aesthetic judgement, such a powerful psychological force, be anyone's guide to
successful
mathematics, despite strong individual differences of opinion? That is the subject of our speculations in the next two chapters.
Hardy on mathematics and chesssuccessful
mathematics, despite strong individual differences of opinion? That is the subject of our speculations in the next two chapters.
G. H. Hardy was a purer-than-pure mathematician who hated war, and a non-conformist who hated religion and regretted even working within the sound of a Roman Catholic church [Hardy
1941
: Intro.]. He claimed, famously, that,
1941
: Intro.]. He claimed, famously, that,
A mathematician, like a painter or poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with
ideas
.
He scorned the application of mathematics to anything at all and once expressed the hope that nothing he had ever discovered would have any practical use. He turned out to be mistaken though to be fair his one deliberate contribution to applied mathematics, the Hardy–Weinberg law
in genetics, was not published as a mathematical paper but sent as a letter to
Science
, which started by saying that, ‘I should have expected the very simple point which I wish to make to have been familiar to biologists’ and went on to refer to the mathematics involved as ‘A little mathematics of the multiplication-table type’ thus putting readers of
Science
in their place [Hardy
1908
].
in genetics, was not published as a mathematical paper but sent as a letter to
Science
, which started by saying that, ‘I should have expected the very simple point which I wish to make to have been familiar to biologists’ and went on to refer to the mathematics involved as ‘A little mathematics of the multiplication-table type’ thus putting readers of
Science
in their place [Hardy
1908
].
Our concern is that Hardy also made an aesthetic link between maths and chess, and mathematical puzzles:
The fact is that there are few more ‘popular’ subjects than mathematics. Most people have some appreciation of mathematics, just as most people can enjoy a
pleasant tune…There are masses of chess-players in every civilised country…and every chess-player can recognise and appreciate a ‘beautiful’ game or problem. Yet a chess problem is
simply
an exercise in pure mathematics…and everyone calling a problem ‘beautiful’ is applauding mathematical beauty…We may learn the same lesson…from the puzzle columns of the popular newspapers. Nearly all their immense popularity is a tribute to the drawing power of rudimentary mathematics, and the better makers of puzzles…use very little else. They know their business; what the public wants is a little intellectual ‘kick’, and nothing else has quite the kick of mathematics.
Hardy is no doubt correct but his claim begs as many questions as it answers. Millions do get a kick out of maths and puzzles – but millions don't. Why not? And how is this ‘kick’ connected to
success
at maths?
success
at maths?
As human beings we get satisfaction both when our expectations are met, and when they are not – when we are surprised! When we look at a visual pattern, or listen to music in which a rhythm repeats and a line of melody returns again and again, our expectations are met and we feel an aesthetic pleasure: but we also get our ‘kick’ when the pattern fails to continue because a different – and maybe deeper – pattern exists.
School pupils who have only graphed straight lines and parabolas are easily impressed when they first meet a curve with asymptotes: instead of heading steadily towards the edge of the graph paper the asymptote races off the page. An asymptote also has the strange feature that the curve gets closer and closer to it, but never meets it – an example of
limits
, another counter-intuitive topic which easily intrigues children.
limits
, another counter-intuitive topic which easily intrigues children.
This double effect of expectations met and expectations surprised is especially strong in mathematics just because our confidence in maths is so strong, so our expectations are perfectly met – except when they are amazingly confounded.
This creates a potential double bind for teachers: their pupils need experience
before
they can develop expectations and then have them confounded: so how can teachers give their pupils beautiful experiences to motivate them from the start? One answer is through the use of mathematical recreations that are already more or less ‘familiar’.
before
they can develop expectations and then have them confounded: so how can teachers give their pupils beautiful experiences to motivate them from the start? One answer is through the use of mathematical recreations that are already more or less ‘familiar’.
Mathematical
objects
and
proofs
give the same effect: a ‘kick’ out of structure and pattern and a ‘kick’ out of surprises, for example when a brilliant and
beautiful
proof introduces an unexpected idea.
objects
and
proofs
give the same effect: a ‘kick’ out of structure and pattern and a ‘kick’ out of surprises, for example when a brilliant and
beautiful
proof introduces an unexpected idea.
On the Continent what we call chess Brilliancy Prizes are, significantly, called Beauty Prizes. They are not won for merely calculating many moves ahead. Tactical brilliance helps but strategical depth is just as important and the greatest masterpieces display both. Alekhine's famous game against Reti [Reti-Alekhine, Baden-Baden 1925] does involve astonishing look-ahead but that's only a small part of its beauty. As the brilliant tactician Rudolph Spielmann exclaimed, ‘I can see the combinations as well as Alekhine, but I can't reach his positions!’ Strategical depth is the
desideratum
. Botwinnik's famous win against then world champion Capablanca in the 1938 AVRO tournament was just such a strategical masterpiece, rather than a display of fireworks.
desideratum
. Botwinnik's famous win against then world champion Capablanca in the 1938 AVRO tournament was just such a strategical masterpiece, rather than a display of fireworks.
In maths, as in chess, mere calculation is not enough. Imagination and insight are necessary to create beauty and, plausibly,
strategical or structural depth
.
strategical or structural depth
.
The rules of the game create structures that have a mysterious beauty simply because they are so hard to discover. Chess players of today appreciate the beautiful balance between the weakness of backward pawns and their dynamic possibilities, but this feature took centuries to discover.
Psychologists have studied the
Aha! experience
: the penny drops and you finally ‘see it’, whatever ‘it’ may be. This is closely related to the ‘kick’ that Hardy talked about and it depends on making connections and spotting surprising relationships, so it depends on structure, and especially on analogy which is especially beautiful, we might say, because you get two patterns for the price of one.
Aha! experience
: the penny drops and you finally ‘see it’, whatever ‘it’ may be. This is closely related to the ‘kick’ that Hardy talked about and it depends on making connections and spotting surprising relationships, so it depends on structure, and especially on analogy which is especially beautiful, we might say, because you get two patterns for the price of one.
Another side of the same coin is that mystery creating a challenge can be beautiful – and when it is clarified it remains beautiful because it has now been illuminated – so once again the mathematician wins both ways.
So does the chess player. Tournament spectators watching a master game on giant boards may be mystified by a certain move or sequence but in the adjoining analysis room another master comments on the play and sooner or later the mystery is elucidated: if it is indeed brilliant rather than an error (even masters make mistakes) then the puzzle and its solution share a linked beauty.
A sense of mystery, however, depends on the mode of presentation. If Pythagoras’ theorem
is displayed as a dry statement about right-angled triangles to pupils who lack the experience to find it surprising, the presentation will fail, but if it is used to predict the distance from one corner of the classroom to the
opposite corner, pupils start by being surprised but, all being well, conclude by understanding as well.
is displayed as a dry statement about right-angled triangles to pupils who lack the experience to find it surprising, the presentation will fail, but if it is used to predict the distance from one corner of the classroom to the
opposite corner, pupils start by being surprised but, all being well, conclude by understanding as well.
Jim Henle has referred to Romantic mathematics as maths that has the qualities of ‘remoteness and strangeness’ and François Le Lionnais distinguished between Classical and Romantic beauty. We might well conclude that the beauty of the Mandelbrot set is Romantic.
Figure 19.1
The Mandelbrot set, with an internal point marked
The Mandelbrot set, with an internal point marked
Figure 19.2
The Julia set
of the marked point
The Julia set
of the marked point
Figure 19.1
shows the Mandelbrot set.
Figure 19.2
shows the Julia set of an internal point, in one piece. When a point is chosen outside the
Mandelbrot set
then its
Julia set
breaks down into separated pieces: the more distant the
point chosen, the more broken-up the Julia set becomes, creating a beautiful and unique Fatou dust
cloud for every external point (
Figure 19.3
).
shows the Mandelbrot set.
Figure 19.2
shows the Julia set of an internal point, in one piece. When a point is chosen outside the
Mandelbrot set
then its
Julia set
breaks down into separated pieces: the more distant the
point chosen, the more broken-up the Julia set becomes, creating a beautiful and unique Fatou dust
cloud for every external point (
Figure 19.3
).
Figure 19.3
Fatou dust [Diagram by John Sharp]
Fatou dust [Diagram by John Sharp]
Other books
No Man's Space 1: Starship Encounter by Nate Duke
Fallen Angel by Melody John
The Seduction Plan by Elizabeth Lennox
Facade by Susan Cory
Luminous by Corrina Lawson
Just One Look by Joan Reeves
Singled Out by Trisha Ashley
Retribution by Gemma James
DARE: A Bad Boy Romance by Carmen Faye
Jamyria: The Entering (The Jamyria Series Book 1) by Madeline Meekins