In the Beginning Was Information (5 page)
Read In the Beginning Was Information Online
Authors: Werner Gitt
Tags: #RELIGION / Religion & Science, #SCIENCE / Study & Teaching
The nine above-mentioned general but fundamental theorems about the nature of the laws of nature, N1 to N9, have all been derived from experience. Their correctness cannot be proved, but can be tested repeatedly in the real world. We now formulate a tenth theorem which depends, however, on the personal view of the user. For this reason we present two different versions, theorems N10a and N10b. In the one case, the existence of God is denied, and in the second case, He is accepted as the Prime Cause. Both views are equally a question of belief and conviction. In the case of any given model, we have to decide which one of the two assumptions would be more useful.
N10a: Natural events can be explained without God.
This assumption can be used in all cases where the laws of nature are applied to existing or planned systems. An analysis of the energy equilibrium when ice melts is an example of an existing system, while an example of a planned system is the building of a new space vehicle. In actual fact, most effects of the laws of nature can be explained and computed without reference to God (e.g., free fall). All attempts to explain the origin of life by means of models where God as initiator is ignored are based on theorem N10a.
It is necessary to formulate an important alternative theorem for those who acknowledge the God of the Bible, namely, when did the laws of nature begin to operate, and what is God’s position in regard to these laws? These questions cannot be solved through observation, and we require some knowledge of the Bible as background.
N10b: The present laws of nature became operational when creation was completed.
The laws of nature are a fundamental component of the world as we know it, and they indicate that the Creator sustains all things (Col. 1:17, Heb. 1:3). These laws were installed during the six creation days, and thus cannot be regarded as prerequisites for creation, since they themselves were also created. It is very emphatically denied that God’s creative acts could be explained in terms of the present laws of nature. At the end of the six days of creation, everything was complete — the earth, the universe, the plants, animals, and man: "By the seventh day God had finished the work he had been doing" (Gen. 2:2).
If one tried to explain the actual creative acts in terms of the laws of nature, one would very soon be trapped in an inextricable net of speculations. This holds both for creationists and for supporters of evolution. The latter endeavor to explain the origin of life by means of laws of nature, but nobody has yet been able to do this! We therefore conclude: All the laws of nature have only been in operation since the completion of creation.
If God is the Creator of the laws of nature, then He himself is not subject to them. He can use them freely, and can, through His omnipotence, limit their effects or even nullify them. The miracles described in the Bible are extraordinary events where the effects of particular laws of nature were completely or partially suspended for a certain period or in a certain place. When Jesus walked on the water (Matt. 14:22–33), He, as the Son of God and Lord of everything, nullified the law of gravity. We read in Matthew 24:29 that "the heavenly bodies will be shaken"(this could also be translated as "the forces of the heavens will be shaken") when Jesus comes again. In the language of physics, this means that the present finely tuned equilibria of the various kinds of forces in the universe will be changed by the Creator, with the result that the orbits of the earth and the moon will become entangled and the stars will seem to move erratically: "The earth reels like a drunkard, it sways like a hut in the wind" (Isa. 24:20).
The moment that historical questions (e.g., about the origin of the world and of life) or future events (like the end of the earth) are considered, then N10a is entirely useless.
2.4 The Relevance of the Laws of Nature
R1: The laws of nature provide us with a better understanding of natural phenomena and events.
Without the laws of nature we would have had a very limited knowledge of the physical, chemical, astronomical, and biological processes occurring in the world around us. The progress of science mostly relies on the fact that fundamental principles are identified and classified, even when different effects are studied.
R2: The laws of nature enable us to make predictions.
Because of N5 and N9, the expected course of observed processes can be predicted. Exactly because of this certainty, it is in many cases possible to compute beforehand what will happen. If, for example, a stone is dropped, one can calculate what its speed will be after two seconds.
R3: The laws of nature make technological development possible.
All engineering constructions and all technical manufacturing processes are based on the laws of nature. The reason why the construction of a bridge, a car, or an aircraft can be planned in advance, is that the relevant laws of nature are known. Without knowledge of the laws of nature, there could have been neither chemical nor pharmaceutical industries.
R4: By means of the laws of nature, it is possible to determine beforehand whether an envisaged process would be realizable or not.
This is a very important application of the laws of nature. Some time ago I received a comprehensive piece of work consisting of many diagrams, calculations, and explanations, from an inventor with the request that the proposed construction should be checked. This person envisioned an extremely complex system of pumps and pipes which would be able to drive a hydraulic motor. It was, however, immediately clear, without my having to do any calculations or tests, that such an arrangement could never work, because it violated the energy law. In many cases, the laws of nature enable one to make conclusions beforehand without having to study the details.
R5: The laws of nature are applicable to cases formerly unknown.
The fact that the laws of nature can be transferred to new cases is of special importance. Up to the present time, nobody has been able to imitate the process of photosynthesis which takes place in every blade of grass. If and when such an endeavor may eventually be planned, then all proposed methods which violate any one of the laws could be rejected in advance. Any such design could be eliminated as useless in the conceptual phase. In addition, past results which were accepted in the light of some paradigm, could also be evaluated. Is it, for example, possible that information could have originated in a postulated primeval soup? This question is discussed further in chapter 6.
R6: One can employ a known natural law to discover another one.
It has happened time and again in the history of science that a new law has been discovered using the validity of a known law. If the law of gravity had not been known, then the behavior of the moons of Jupiter could not have been investigated properly. Observations of their motions made it possible to compute the speed of light, which is an important physical constant.
The orbits of the planets cannot be exactly elliptical (as would be required if the gravitational pull of the sun was the only force acting on them), as required by Newton’s law, since they are not only under the gravitational influence of the sun, but they also affect one another gravitationally to a lesser extent. John Couch Adams (1819–1892), a British astronomer and mathematician, computed the expected perturbations caused by their mutual gravitational attractions, of the orbits of the then known major planets, Jupiter, Saturn, and Uranus. The French astronomer Urban J.J. Leverrier (1811–1877) also computed the deviations of these orbits from the perfect Kepler ellipses independently. It was found that Jupiter and Saturn "lived up to the expectations," but Uranus exhibited deviant behavior.
Relying on the validity of Newton’s law, both astronomers were able to deduce the position of a hitherto unknown planet from these irregularities. Each of them then approached an observatory with the request to look for an unknown planet in such and such a celestial position. This request was not taken seriously at one observatory; they regarded it as absurd that a pencil-pusher could tell them where to look for a new planet. The other observatory responded promptly, and they discovered Neptune. Leverrier wrote to the German astronomer Johann Gottfried Galle (1812–1910), who then discovered Neptune very close to the predicted position.
2.5 The Classification of the Laws of Nature
When one considers the laws of nature according to the ways they are expressed, one discovers striking general principles which they seem to obey. The laws can accordingly be classified as follows.
Conservation theorems:
The following description applies to this group of laws: A certain number, given in a suitable unit of measurement, can be computed at a specific moment. If this number is recomputed later after many changes may have occurred in nature, its value is unchanged. The best-known law in this category is the law of the conservation of energy. This is the most abstract and the most difficult of all the conservation laws, but at the same time it is the most useful one, since it is used most frequently. It is more difficult to understand than the laws about the conservation of mass (see footnote 5), of momentum, of rotational moment, or of electrical charge. One reason is that energy can exist in many different forms, like kinetic energy, potential energy, heat energy, electrical energy, chemical energy, and nuclear energy. In any given process, the involved energy can be divided among these forms in many different ways, and a number can then be computed for each kind of energy. The conservation law now states that the sum of all these numbers stays constant irrespective of all the conversions that took place during the time interval concerned. This sum is always the same at any given moment. It is very surprising that such a simple formulation holds for every physical or biological system, no matter how complex it may be.
Equivalence theorems:
Mass and energy can be seen to be equivalent in terms of Einstein’s famous formula E = m x c
2
. In the case of atomic processes of energy conversion (nuclear energy) there is a small loss of mass (called the deficit) which releases an equivalent amount of energy, according to Einstein’s formula.
Directional theorems:
From experience in this world we know that numerous events proceed in one sense only. A dropped cup will break. The converse event, namely that the cup will put itself together and jump back into our hand, never happens, however long we may wait. When a stone is thrown into a pool of water, concentric waves move outward on the surface of the water. This process can be described mathematically, and the resulting equations are equally valid for outward moving waves and for the imaginary case if small waves should start from the edge and move concentrically inward, becoming larger as they do so. This converse process has never been observed, although the first event can be repeated as often as we like.
For some laws of nature, the direction does not play any role (e.g., energy), but for others the process is unidirectional, like a one-way street. In the latter case, one can clearly distinguish between past and future. In all cases where friction is involved, the processes are irreversible; they proceed in one direction only. Examples of such laws are the law of entropy (see the appendix), the chemical principle of Le Chatelier (Henry-Louis Le Chatelier, French chemist, 1850–1936; see Q20 p. 128–130), and the law of mass action.
Impossibility theorems:
Most laws of nature can be expressed in the form: "It is impossible that…." The energy law for example, can be stated as follows: "It is impossible that energy can come into existence by itself." R. Clausius formulated the second law of thermodynamics as an impossibility: "Heat cannot of itself pass from a colder to a hotter body" The impossibility theorems are very useful, because they effectively distinguish between possible and impossible events. This type of scientific formulation will be encountered frequently when we come to the information theorems.
Geometrical impossibilities can also be devised. Three different geometric representations appear in Figure 6, but such bodies are just as impossible to construct as it is to expect results that are precluded by laws of nature.
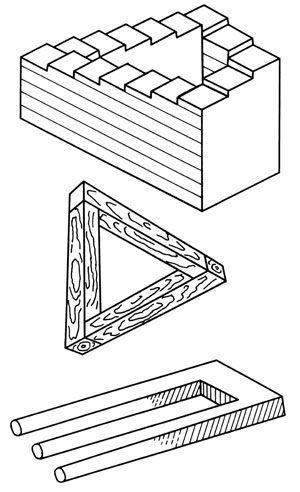
Figure 6:
Geometrically impossible bodies.
Laws which describe processes:
If the future (prognosis) or the past (retrognosis) states of a system can be described when the values of the relevant variables are known for at least one moment in time, such a formulation is known as a process law. A typical physical example is the description of radioactive decay.
Co-existence laws:
These describe the simultaneous existence of the properties of a system. The formula describing the state changes of an ideal gas, p x v = R x T, is a typical physical co-existence law. The values of the three quantities, pressure p, specific volume v, and absolute temperature T, comprise a complete description of the "state" of an ideal gas. This means that it does not depend on the previous history of the gas, and neither does it depend on the way the present pressure or the present volume has been obtained. Quantities of this type are known as state variables.