Jacquards' Web (11 page)
Authors: James Essinger
The German mathematician Gottfried Wilhelm Leibniz saw Pascal’s machine while on a visit to Paris and worked to develop a more advanced version. Pascal’s device was only able to count, whereas the instrument Leibniz developed was designed to multiply, divide, and could even extract square roots. He completed a model of the machine in
1673
and exhibited it at the Royal Society, but Leibniz’s device did not work properly either and was never anything more than a curiosity.
68
The Difference Engine
Pascal’s and Leibniz’s machines differed in one vitally important respect from the one Babbage planned. Theirs were manual devices, but Babbage was adamant from the outset that his own calculation machine would be
automatic
. Unlike Pascal’s and Leibniz’s apparatuses, which required meticulous human intervention every stage of the way, the machines Babbage conceived as a result of his determination to build a contrivance that would calculate tables ‘by steam’ were designed to produce column after column of results
themselves
, with the operator only having to turn the handle that powered the machine. It was, in other words, automatic. Even the handle-turning process could have been mechanized: there was indeed no reason why a small steam engine could not have been connected to the machine to do the job. Such a development would have answered Babbage’s cry of frustration with a practical reality.
Babbage made the important practical decision about the technology at the heart of his planned calculation machine early on in his deliberations, very likely during the first week or so following his frustrated exclamation during his work with Herschel. This decision was to build his machine from cogwheels.
In the
1820
s, when the science of electricity was still in its infancy and when the science of electronics, which concerns itself with the behaviour of the very particles of which electricity is composed, still lay a century in the future, Babbage had little choice but to use a mechanical technology for building his machines.
Unfortunately, he left no explicit explanation of why he decided to opt for cogwheels. But it is not difficult to guess the grounds of the decision. It is clear that cogwheels were the only technology he could imagine to be equal to the demands of the project.
Why? Because, firstly, a cogwheel is by definition a gear-wheel. It consequently facilitates the meshing with another cog-69
Jacquard’s Web
wheel that Babbage saw could form the hub of the addition process at the heart of the machine he planned. Secondly, and equally importantly, a cogwheel allows the transmission of energy in regular, incremental steps. It is precisely this attribute which makes cogwheels essential in mechanical clocks. They are an essential part of the
escapement
, a device in a clock or watch that alternately checks and releases the train (i.e. the connected elements of the mechanism) by a fixed amount and transmits a periodic impulse from the spring or weight to the balance wheel or pendulum. The relationship between cogwheels and a clock’s mechanism seems natural enough to us now, but like most major breakthroughs in science it took place less through inspiration than through necessity. The use of cogwheels in clock mechanisms appears to have derived from the first attempts—probably made sometime in the tenth or eleventh centuries—to build a clock that would be driven by a falling weight.
For the early clockmakers, a controlled falling weight on the end of a piece of cord was an obvious and reliable driving force to power a clock. It was, however, soon discovered that simply letting a weight fall and allowing this to turn an axis which in turn operates a clock does not actually work. The reason is that a weight accelerates as it falls. A clock driven by a simple falling weight would run faster and faster, like a clock face in a speeded-up movie. Even if a brake is used to slow the weight down, practical experience shows that the brake gradually wears away and becomes progressively smoother, causing the velocity of the weight to increase.
It is not known exactly when this problem was solved. But sometime early in the fourteenth century, an unknown genius had the idea of using a cord to connect a falling weight—whose fall was itself controlled by a speed governor—to a wheel that carried short, horizontal, uniformly spaced pegs around its circumference. These pegs meshed with an axis that was also equipped with such pegs. When the weight fell, the turning of 70
The Difference Engine
Folios and balance
weights
Verge
Palettes
W
A pegged wheel meshing with another in an early clock.
the wheel was carried out at a regular rate because the inertia of the weight itself checked the wheel’s rotation. This permitted the energy transmission to be regular and uniform, making possible the construction of clocks which work in a regular and measured way.
Eventually, it was understood that the wheel with pegs on it could be replaced by a metal cogwheel, and that this wheel would not only be more durable than a wooden one, but could also be made much smaller. As the centuries passed, the technology of clock-making became highly sophisticated. Indeed, some of the clocks of the seventeenth and eighteenth centuries are of such mechanical sophistication that they act as powerful correc-tives to the modern inclination to view the science and technology of the past with a kind of amused condescension.
71
Jacquard’s Web
The advent of electric and electronic timepieces during the twentieth century tended to restrict modern clockwork mechanisms to very large clocks, or luxury watches, but some great feats of clockwork were achieved in that century none the less. For example, the Jens Olsen Astronomical Clock, displayed in Copenhagen Town Hall, Denmark and set in motion on
15
December
1955
, possesses the slowest clockwork mechanism in the world. Its movements model just about every conceivable astronomical motion that one might wish to model. In particular, the so-called ‘celestial pole’ of the clock, mimicking the extremely slow precession of the Earth’s axis in relation to the stars, will take
25 753
years to complete just one revolution.
Charles Babbage would no doubt have enjoyed the idea of such a clock. When he started work on trying to build a cogwheel calculator he was able to benefit from clock-makers’
knowledge of producing cogwheels. Babbage designed his Difference Engine to use many thousands of metal cogwheels in order to perform calculations. No clock had ever employed anything like as many cogwheels as this, but Babbage was confident in his own scientific and engineering powers, and was sure he had a good chance of success.
Babbage called his first calculating machine the Difference Engine because it used a mathematical technique called the Method of Differences. This is a technique to calculate mathematical tables by repeated regular additions of the ‘differences’
between successive items in a mathematical series. A mathematical series is a set of terms in ordered succession, the value of each being determined by a specific relation to adjacent terms.
Mathematical series can be generated by a mathematical formula.
To take a simple example, the numbers
1
,
2
,
3
,
4
,
5
, and so on, to infinity comprise the mathematical series requiring
1
to be added to each previous term. Mathematical tables such as logarithmic tables can also be generated by a mathematical formula.
72
The Difference Engine
The beauty of the Method of Differences is that it simplifies the process of calculating a long and complex mathematical series. In essence, it allows otherwise difficult multiplications to be replaced by numerous straightforward but monotonous additions. But, of course, if a machine is carrying them out, their monotony does not matter. Interestingly, Babbage’s approach to calculating mathematical tables was basically the same as that chosen by Gaspard de Prony. The Frenchman also made use of the Method of Differences, and as we have seen hired unemployed hairdressers to complete the simple but numerous calculations necessary. Babbage was essentially mechanizing this process.
Babbage’s mechanization was based on the idea that teeth on individual cogwheels (described as ‘Figure Wheels’ by Babbage) would stand for numbers, and that the machine’s operation would be based around meshing independently moving Figure Wheels arranged in vertical columns with each other. This meshing process would carry out an arithmetical calculation.
Babbage decided to use the familiar, everyday counting system (base
10
) for his machine. He arranged things so that the Figure Wheel at the bottom of a vertical column would represent the units, the Figure Wheel second from the bottom the tens, the Figure Wheel third from the bottom the hundreds, and so on.
For example, the setting of a four-digit number such as ‘
6538
’
would require the bottom Figure Wheel to be turned eight teeth to represent ‘
8
’—that is, the number of
single units
; the second Figure Wheel from the bottom to be turned three teeth to represent ‘
3
’—that is, the number of
tens
; the third Figure Wheel from the bottom to be turned five teeth to represent ‘
5
’—the number of
hundreds
; and the fourth Figure Wheel from the bottom to be turned six teeth to represent ‘
6
’—the number of
thousands
. On this occasion all the Figure Wheels above the fourth wheel would be set to zero, as they were not required.
The value of any number was therefore capable of being set in the machine in a vertical stack of cogwheels as long as there were enough wheels in the vertical stack to cover the tens, thou-73

74
The Difference Engine
sands, tens of thousands, hundreds of thousands, millions, etc.
that were required.
In his own lifetime Babbage never succeeded in completing a Difference Engine. The closest he came was building one-seventh of a Difference Engine. This one-seventh is essentially a demonstration piece. It is this portion, finished in
1832
, that was the other main conversation piece at his soirées apart from the woven portrait of Jacquard.
Why exactly did Babbage fail to complete a working model of the Difference Engine during his own lifetime? To understand this, we need to understand how Babbage went about his work.
With nothing but the mechanical engineering of his own age to provide him with the tools he needed, he was obliged to imagine and improvise from scratch the components he needed for his revolutionary machine. Many of the parts he designed were wonderfully complex, especially in light of the fact that nothing comparable had ever been seen before.
Babbage designed these and numerous other components without any certain initial knowledge that they would work. He took great efforts to test his designs, often making the components out of cardboard to verify their action before having them made in metal. He was a pioneer in mechanical engineering.
But unfortunately, the lack of standardization in the component manufacture at the time meant that no component could be precisely identical with the previous one, which would of course have been the ideal. It was true that parts could be manufactured nearly identically by finishing them with hand tools or by additional machining, and could subsequently be made to fit in the machine by additional filing and tweaking. But this process was labour-intensive, time-consuming, and expensive. Babbage could have benefited enormously from the existence of a precision metal industry, but there wasn’t one in his day.
Babbage employed a brilliant toolmaker and draughtsman named Joseph Clement to work on the components. Clement’s (
right
) This portion of the Difference Engine, completed by Babbage and his engineer, Clement, is one of the scientific wonders of the nineteenth century.
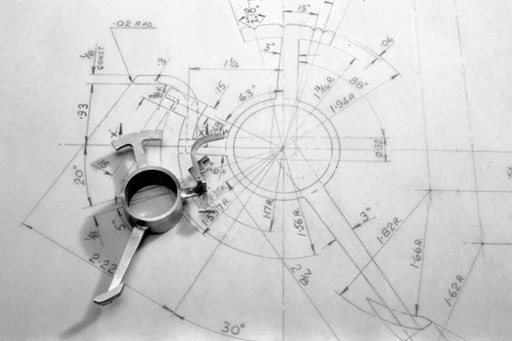
Jacquard’s Web
A modern piece-part drawing of a Difference Engine component showing the remarkable complexity of Babbage’s concept and the finished component built by modern precision engineering.