Mathematics and the Real World (52 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein
Since the Greeks made mathematics into a discipline based on axioms and logical rules of inference, mathematicians have viewed those as the solid foundation on which mathematics is based. Initially the axioms reflected physical truth, or ideal mathematical truth, which cannot be disputed. Later, the concept of an axiom was interpreted more widely, and lists of competing axioms were examined. Modern mathematics also allows mathematical developments under different lists of axioms that contradict each other with the intention of comparing the mathematical conclusions deriving from the various axioms. Be that as it may, the generally accepted assumption was that developments that fulfilled the criteria of the logical rules of inference could be relied upon. At the same time, as intuition that developed in the course of evolution is inconsistent with a significant part of the logical elements used in mathematical analysis, in many mathematical developments throughout the ages mathematicians ignored the strictness demanded by the logical method so that in day-to-day research
both definitions and proofs relied only on intuition or formalism, without relating to the framework of logic. Here are few examples.
The Greeks had come across negative numbers, but they rejected them as being unacceptable. The mathematician Diophantus of Alexandria, who lived in the third century CE, published methods of solving algebraic equations, and in a formal way found solutions that were negative numbers. However, he did not accept them as real solutions to the equations. The reason was integral to the approach that led the Greeks to a definition of numbers that was geometry based: every number reflects a length of a section that can be related to a length of one unit. A rational number, say , is the length of a section that is five times as long as a third of a section of unit length. An irrational number, say √2, is the length of the diagonal of a square with sides of length one unit. All these are intuitive geometrical definitions based on a system of axioms that the Greeks considered perfect. In such a system, there is no room for negative numbers.
, is the length of a section that is five times as long as a third of a section of unit length. An irrational number, say √2, is the length of the diagonal of a square with sides of length one unit. All these are intuitive geometrical definitions based on a system of axioms that the Greeks considered perfect. In such a system, there is no room for negative numbers.
Later on, the Indians permitted the use of negative numbers for purposes of solving problems. For example, a number can be written as negative on one side of an equation and can be transferred to the other side, but they too did not recognize negative numbers as independent mathematical entities. The Arab mathematician Abu Ja'far Al-Khwarizmi, whom we mentioned in connection with the discussion of algorithms, also allowed the use of negative numbers as a means of carrying out calculations, but he denied negative numbers the right to their own existence. Over time, many others used negative numbers to solve problems, and the method became embedded in mathematical practice, but those numbers were not accepted as legitimate entities. The debate over what they were also occupied mathematicians in the seventeenth century, who, although they used negative numbers, did not agree among themselves about various arithmetic operations involving those numbers. Leibniz pondered over the result of multiplying two negative numbers, or dividing 1 by negative 1. Euler proposed the solution (–1) × (–1) = 1 to preserve the rules of multiplication but with no logical or intuitive basis. This disagreement persisted until the eighteenth century and beginning of the nineteenth century.
Augustus De Morgan (1806–1871), one of the best-known mathematicians
of his time, used the following exercise to explain why negative numbers are of no significance. A fifty-six-year-old man has a son aged twenty-nine. When will the father be twice as old as his son? Simple arithmetic that any schoolchild today can do easily shows that the answer is –2, and we understand that to mean that two years ago the father was twice as old as his son. In the nineteenth century, however, De Morgan's conclusion was that the answer –2 was absurd. At the same time he argued that the question could be put differently and the correct answer obtained. That is, the question should be how many years ago was the father's age twice that of the son, and then the answer is 2. The approach accepted today, that the numbers are ranged along an infinite axis, with the negative numbers measuring the distance along what is called the negative direction, is a relatively modern one. Thus, we see that the negative numbers were developed independently in different places around the world, and they were used as an efficient tool for solving mathematical problems for a long time before they were recognized as representing a mathematical basis worthy of being defined by axioms.
Another example of a concept that preceded a logic-based system is that of complex numbers. These are numbers in the form of
a
+
ib
, where
a
and
b
are real numbers, and
i
is the square root of negative 1, that is,
i
= √–1. These also appeared as formal expressions in solutions of algebraic equations. For example, the equation
x
2
+ 1 = 0 has no real-number solution, but both
i
and –
i
are solutions to the equation. Today this number system is well known and is used for various purposes, including the description of natural phenomena. There are also axioms that describe the system of complex numbers, but mathematicians were using complex numbers long before the system of axioms was constructed. One of the first to use them was Gerolamo Cardano, of whom we wrote in section 36, who was famous for solving polynomial equations and proposed complex numbers as a solution without explaining what those numbers are and without referring to axioms. Others developed the system further, but as in the case of negative numbers, many members of the scientific community opposed the adoption of the concept that complex numbers were legitimate numbers. Descartes, for example, was among the opponents, saying that such a solution
had no significance, and he called
i
an imaginary number, intending that as a term of denigration. The name stuck, and is still used, but without any negative connotations. Neither did Newton, later on, accept those numbers as legitimate. Today complex numbers are used as a convenient description of mechanical systems that Newton himself analyzed and developed, a possibility that did not occur to him. Later, the arithmetic of complex numbers was developed formally, and many additional uses were discovered. The logic of complex numbers, together with the axioms that define them, was determined only in the nineteenth century, but that did not prevent its use much earlier.
Infinitesimal calculus as developed by Newton and Leibniz also lacked a base in logic accompanied by appropriate axioms. We have spoken of the article by Bayes that defended Newton's theory against the bitter attacks made by Bishop Berkeley. The latter, and others, denied infinitesimal calculus, as it was constructed without a basis in logic. The attack was given some support because of the fact that infinitesimal calculus was developed without regard to the normal rigorous mathematical approach, as a result of which many blatant errors were made and revealed. Newton and Leibniz defined the derivative of a function at a given point as the rate of change of the function at that point. The geometric expression of that rate of change is the slope of the tangent to the function at that point. They used the term
the tangent
, with the definite article
the
. They applied that definition to every function and at every point, ignoring the question whether a tangent exists. It is easy to find functions that do not have tangents at particular points, for instance, the function that ascribes to a number its absolute value (this is generally written as │
x
│) does not have a tangent at 0 and therefore does not have a derivative at that point. Perhaps we could come to terms with this example by ignoring the single point 0, but it is more difficult to satisfy intuition regarding derivatives in the case of the example given by Karl Weierstrass (1815–1897), one of the most highly respected German mathematicians. He presented a continuous function that did not have even a single tangent. The statement by Émile Picard (1856–1941) is quoted with good reason: If Newton and Leibniz had known of Weierstrass's example, infinitesimal calculus would not have come into being.
Thus, more than a hundred years passed before mathematicians undertook the task of proposing a more rigorous framework for infinitesimal calculus founded on accepted logic.
58. RIGOROUS DEVELOPMENT WITHOUT GEOMETRY
It was not until the nineteenth century that the mathematical community began to become involved in a reexamination of the logical basis of mathematics and the degree of rigor in its development. The words
not until
are used advisedly, as for thousands of years from the development of mathematics by the Greeks mathematicians relied on their intuition and were certain that it was consistent with the system of axioms determined by Euclid. This does not mean that the status of the axioms was totally ignored. There were sporadic attempts to check the compatibility of the axioms or to replace some of them with others, but these attempts focused on specific subjects, such as the discussion of the parallel-lines postulate discussed in section 27. Mathematicians in general did not consider it necessary to perform an overall examination of the foundations of mathematics.
Two interrelated factors brought about the realization that the concepts that mathematics had used for a long time and the axioms underlying mathematics should be reexamined. One was the growing number of definitions that were not sufficiently clear, definitions that even caused errors that were discovered in the use of infinitesimal calculus. Newton's formulation, specifically the use of fluxion as the basis for the description of the change of direction of a function, may have been appropriate for his own intuition, but it was thwarted many others. Leibniz's formulation, the division of infinitesimal quantities of the form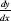 was convenient to use, but it did not relate to the essence of the infinitesimal quantities, and mathematicians developed intuitions about them that often resulted in errors. Both approaches, that of Newton and that of Leibniz, and in their wake all the following developments of the theory, were based on geometry.
was convenient to use, but it did not relate to the essence of the infinitesimal quantities, and mathematicians developed intuitions about them that often resulted in errors. Both approaches, that of Newton and that of Leibniz, and in their wake all the following developments of the theory, were based on geometry.
Then the second factor appeared, highlighting the need for renewed
study of basics. The logical foundations of geometry throughout the generations were considered stable and thus not in need of examination and checking. And then, as described in section 27, questions and doubts arose at the beginning of the nineteenth century regarding the validity of the axioms that constituted the basis of geometry. The questions asked related to the absolute correctness of axioms that describe the geometry of nature, as well as to their logical completeness. For example, Euclid relates to the situation in which two points lie one on each side of a straight line. When we encounter such a description, a clear picture immediately comes into our minds of a straight line with a point on either side. But what are the two sides of the straight line? Their existence does not derive from the axioms. Imagine a long tube, and imagine a straight line drawn along its length. Does that straight line actually have two sides? Such doubts led mathematicians, with the leading French mathematician Augustine-Louis Cauchy (1789–1857) at their head, to redevelop differential and integral calculus, but this time based on the system of numbers and not on geometry.
We will not delve here into the details of the developments but will just illustrate one concept. As stated, for Newton, Leibniz, and their followers the derivative was defined as the slope of the tangent of a function at a point. A tangent and its slope are clearly defined in geometry. To define them using numbers alone, Cauchy used as a basis a precise formulation of the concept of the limit of a sequence of numbers. Archimedes had already related explicitly to the concept of a limit, but without defining it. Cauchy defined a limit as follows:
The number
z
is the limit of a sequence of numbers
x
n
if for every number
ε
greater than zero there is an index
m
such that for every index
n
greater than
m
the distance between
x
n
and
z
is smaller than
ε
.