Mathematics and the Real World (55 page)

During the development of this elegant theory, some troubling questions arose. For example, is there a power greater than that of the natural
numbers and smaller than that of the continuum? In mathematical notation the question is, does C =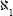
? This question greatly perturbed Cantor himself and generations of mathematician who came after him until the answer was found in 1964, as we will describe below. Another question was, what happens to the set of all sets? It was always clear that there was no natural number that was the largest of all numbers. With any number, 1 can be added to it, and a larger number will be obtained. When examining sets, however, the question can be asked, what is the power of the set whose elements are all the sets in the world? Such a property would ensure that the power of that set is the greatest possible. On the other hand, Cantor proved that for every set that is not empty, and hence also the set of all sets, the power of the collection of its subsets is greater than the power of the set itself. We seem to have arrived at a contradiction. It was solved by the decision that not all sets are “legitimate” from the aspect of the new mathematics. Thus, the set of all sets, although we have called it a set, is not a set in the sense that we can apply the new mathematics to it, just as the arithmetic of the natural numbers cannot be applied to infinity.

That was the situation toward the end of the nineteenth century and at the beginning of the twentieth. Natural numbers were defined by sets. Then, as we have seen, the positive rational numbers could be defined, followed by the negative rational numbers (we spared the reader the detailed description of that stage). Next, the irrational numbers could be defined by means of Dedekind cuts, which were themselves defined as sets of power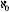
and were thus permitted infinite sets. From there it was possible to continue to derivatives, integrals, and the rest of mathematics. Operations in logic, and in particular the laws of inference, could also be explained in terms of sets. At that time it seemed that the solid foundations of mathematics had been found that would replace the shaky foundations set by the Greeks.

In this context another important new development took place in understanding the concept of an axiom. For the Greeks, axioms expressed agreed properties of entities in nature. As such, the axioms related to familiar concepts, such as points and straight lines, which the mathematicians defined rigorously. The problem is that the definition itself uses concepts that have
not themselves been defined. Here the question reappears: To what extent are the defined entities self-explanatory? The answer, on which there was a consensus in the nineteenth century, was that the axioms relate also to abstract entities, which do not need to pertain to anything recognized and defined but just need to be denoted, say, by letters,
x
,
y
,
A
,
B
, and so on. When we want to apply abstract mathematics, we must ascribe to undefined quantities a reference to known entities. If the explanation conforms to the axioms, the mathematics to be developed in line with the axioms will indeed describe reality. Unlike with the Greeks, however, in the mathematics of the nineteenth century, the elements dealt with by the axioms could have nothing to do with nature or with other uses. Speaking of elements that at the outset have no explanation, the English mathematician-philosopher Bertrand Russell (1872–1970) described a mathematician as a person who does not know what he is talking about, nor does he care whether what he is saying is true. Not knowing what we are talking about refers to entities that mathematics deals with that from the outset have no explanation or use. Not knowing whether what we are saying is true refers to truth for a particular purpose, for instance, in nature. In other words, the mathematician can engage in mathematics without any explanation and without being at all interested in an explanation of the entities he is analyzing. Despite Russell's humoristic note, and despite the agreement that axioms relate to abstract entities that are not represented in nature, I do not know mathematicians who can discuss and analyze what can be derived from the axioms without having in mind some sort of representation of a system that fulfills the axioms, except in limited and extreme cases. As we have seen, the human brain is incapable of relating intuitively to logical systems that are completely abstract.

The attitude of the leading mathematicians of the time, at the turn of the century (nineteenth to twentieth), to the basing of mathematics on set theory is interesting. Of particular interest is the reaction of the most famous mathematicians of that period, the German David Hilbert, and the Frenchman Henri Poincaré.

Hilbert (1862–1943) was born in and studied in Königsberg, Prussia
(today the Russian city Kaliningrad), then moved to Göttingen, where he remained until the end of his life. In his lifetime he saw regimes in Europe change several times, and he died while the Nazis were in power. He was not one of their supporters, and after 1933 he tried to help persecuted Jewish mathematicians and physicists, even though at that time he was no longer at his prime. A leading figure in the Nazi regime turned to Hilbert in the course of an official dinner and said, “Herr Hilbert, at last we have rid ourselves of the Jews who contaminated German mathematics.” Hilbert's reply was, “Yes, sir, but since the Jews have left, mathematics has ceased to exist in Germany.” He made many contributions to mathematics in various spheres. He was responsible for fundamental developments, in particular the abstraction of concepts and methods, and was interested in logic and the foundations of mathematics. He made a major impact on mathematics worldwide. When he was invited to deliver the keynote lecture at the Second International Congress of Mathematicians in 1900, instead of presenting his own achievements, as usually happened at such congresses, Hilbert chose to present a list of unsolved problems in mathematics, which he predicted would become the central mathematical problems of the twentieth century. Those problems did indeed feature in research in mathematics throughout the twentieth century; some were solved relatively quickly, and others are as yet unsolved and await solutions in the twenty-first century.

Henri Poincaré, who featured in our discussion of the events that led to the development of the theory of relativity, actually came from the field of engineering. He studied in the École des Mines (a mining, or engineering, school), which was and remains a highly prestigious school in France. His abilities were discovered when he was very young, and he was elected to the French Academy, taught at the Sorbonne, and was possibly the most influential French mathematician of his time. One of his nonacademic activities was engaging in the defense of Alfred Dreyfus at the appeal stage of the famous trial. He and his colleagues, the mathematicians Paul Appel and Jean Gaston Darboux, examined the evidence and declared in a written report submitted to the court that probability theory showed that the charges did not hold up under serious scientific examination. In
his private life Poincaré exhibited great courage in other situations too. In mathematics he was active in mathematical physics and dynamics. His career surged when in the context of a competition announced by the king of Sweden he promoted the understanding of the three-body problem, that is, the dynamics of three or more bodies in space, for instance, the Sun and the planets. In his research he discovered and characterized the dynamic behavior that results in what is studied today in the context of chaos theory.

Hilbert enthusiastically adopted the new developments in understanding the axioms and their connection to logic. He himself drew up a series of geometry axioms, which refined Euclid's axioms, and succeeded in showing that they do not depend on unreliable intuition, nor do they contain internal contradictions. Poincaré also adopted the dependence on logic with enthusiasm and actually said that logic is the material that disinfects mathematics by inhibiting errors. Nevertheless, with regard to the use of sets as the basis of mathematics, opinions were divided. Hilbert declared that set theory is the crowning achievement of man's creativity. Poincaré is reputed to have declared that set theory is a sickness that mathematics will be cured of. We will see the effects of this dispute on the status of set theory when we discuss matters related to the teaching of mathematics, in the
last chapter
of the book.

60. A MAJOR CRISIS

With the exception of a relatively small group of mathematicians, the mathematics community welcomed the reliance on set theory with open arms. Gottlob Frege (1848–1925), a leading German mathematician at the beginning of the twentieth century, decided to put in writing the set theory basis of mathematics. He published the first tome and was in the latter stages of the second when the crisis erupted. Bertrand Russell wrote him a dramatic letter and set out the famous paradox he had discovered in Frege's text, a paradox that led Frege to halt the publication of the second part of his book. For a while Frege tried to correct the theory he had developed but eventually decided to abandon the project he had undertaken.
Bertrand Russell was then a young mathematician whose astuteness had already earned him a reputation in Britain. He was later acknowledged as one of the founders of analytic philosophy and was known for his radical social and political views. He was a pacifist, a conscientious objector in the First World War, and bitterly critical of totalitarian regimes throughout the world. In 1950 he was awarded the Nobel Prize in Literature for his writings in which he championed humanitarian ideals and freedom of thought and for his famous bestseller
A History of Western Philosophy
.

Russell's paradox was in fact a variation on a paradox known already in the time of the Greeks, the liar's paradox. A person says of himself, “I am a liar.” Can we believe him? If his statement is untrue, he is telling the truth, so he is a liar. If it is true, then he is a liar, so we cannot believe him and he not a liar. We have a paradox. Likewise with regard to sets, claimed Russell; define a set such that it contains all sets that do not include themselves as one of the members of the set. Does such a set include itself as one of its elements? If not, it is itself a member of the set and therefore includes itself. If it includes itself, then by the definition of the set it is not one of its elements. A paradox.

Russell's paradox could have been solved in the same way as the Greeks solved the paradox of the liar and similar paradoxes. The solution is to determine that a statement in natural language relating to itself is not acceptable, and it is not legitimate to analyze it by mathematical means. This rule can also be adopted with regard to sets. Just as the set of all sets was excluded from being a set that can be analyzed mathematically, it can be decided that a set whose definition relates to itself is not a “legitimate” set, and the set that Russell used in the paradox was such a set. However, Russell's paradox raised a more fundamental problem, one that even the Greeks were unaware of. We will examine again one of the basic laws of inference, the law of excluded middle.

For every claim P, either P holds or P does not hold.

As this rule of inference relates to itself, among other things, it is not acceptable! The removal of this rule of inference from the area of mathematics
is too great a blow for the mathematics community to bear. One reason is that the method of proof via contradiction is based on this rule. Abolishing all the claims that were based on this system means going right back to square one, including, for example, placing a question mark by the discovery in Pythagoras's time that the number √2 is not rational (see section 7) and also doubting a large part of mathematics developed since then. It was clear that this proposed method of solving the paradox would not work, so there was an urgent need to get to the source of the problem and to reexamine the foundations of mathematics.

The attempts to reconstruct the foundations of mathematics focused on three main avenues.

The first was proposed by Bertrand Russell himself, together with his colleague the well-known English mathematician and philosopher Alfred North Whitehead (1861–1947). They realized that elimination of sets or logical claims would not yield the desired results. Instead, they decided to define what is a permitted system of logic, and they started with a very delicate classification of permitted logical claims, constructing the permitted structure of logic “from below.” They called the permitted bases “types,” and constructed a theory of types from which all mathematics could be developed. Whitehead and Russell began to write their theory and published the first parts in a weighty tome, from which it would eventually be possible to develop mathematics. Its title was
Principia Mathematica
. Their monumental project was never completed, because the approach was too complex. For example, the proof of the equality 1 + 1 = 2 did not appear before page 362. Clearly such a system could not play a future role in a vibrant mathematics.