Mathematics and the Real World (56 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein
A second approach, called intuitionism, was developed by a group of mathematicians led by the Dutchman Luitzen Brouwer (1881–1966). The mathematics that this approach allowed was limited to concrete constructive operations. For example, if you wish to show that a geometric body that has certain properties exists, you must point to it directly. Inferring that the body exists from indirect evidence is not acceptable as proof. In particular, according to this approach the method of proof by contradiction
is not acceptable. Brouwer and his colleagues managed to reconstruct a large part of mathematics in accordance with their approach, but the awkwardness in mathematical practice deriving from that method, together with the need to relinquish many results in the existing mathematics, led to the non-adoption of the method by the mathematics community. Hilbert himself was strongly opposed to intuitionism, repeating and emphasizing that proof by contradiction is at the core of mathematics.
The third avenue pursued was the one accepted by mathematicians as a whole. The idea of basing the structure on sets remained, but like Whitehead and Russell's approach of constructing logic from the foundations, instead of declaring which sets are not permissible and risking future encounters with other paradoxes, here the construction is “from the very core.” We start with permitted sets and, via specific building axioms, we show which sets can be formed from those already in existence. Only sets that can be constructed via the axioms are “legitimate” from the aspect of mathematical analysis. It was Ernst Zermelo, of whom we wrote with regard to his contribution to game theory, who presented these axioms, and they were completed later by Abraham Halevi Fraenkel.
Zermelo was a German mathematician who studied in Berlin, worked for some years in Zurich, returned to Germany, to the University of Freiburg, but resigned in 1936 in protest against the Nazi regime's treatment of the Jews. After World War II he was reinstated to his honorary professorship in Freiburg. Abraham Halevi Fraenkel was also born in Germany, where he published his work on the foundations of set theory and reached the position of professor. He was an active Zionist, and in 1929 he immigrated to pre-State Israel (then Palestine), joined the Hebrew University of Jerusalem, and worked there for the rest of his life.
The system of axioms developed by Zermelo and completed by Fraenkel were named the Zermelo-Fraenkel axioms. The axioms themselves are too technical to be of interest to the general public, and we will not present them here, but once they were put forward and tried on a range of problems, it seemed that hope had been reawakened that mathematics could be based on set theory. In addition to the set-theory axioms, other specific systems of axioms were also being examined, for example, the axioms of the natural
numbers developed by the Italian mathematician Giuseppe Peano (1858–1932). Those axioms are quite simple and incorporate some self-evident statements, such as: the rule that the number 1 exists, the rule stating every natural number is followed by a number that is larger than it by 1, the rules of how to add and multiply and how to use induction, which is actually an independent axiom. The system is simple, and its purpose is to show that mathematics can be based on simple axioms, and those axioms can also be translated into terms related to sets. We mentioned above that Euclid's geometric axioms also underwent a reexamination that was led by Hilbert himself. It seemed that the new versions are free from lack of clarity and the errors of the mathematics of Euclid and his followers.
Alongside the efforts to improve the axiom systems, emphasis was also placed on understanding the properties that a system of axioms should have in order to make it acceptable. As mentioned, for the Greeks, axioms reflected absolute unassailable truths. The more modern approach permitted alternative systems of axioms and even systems that contradict each other. It was therefore important for all of that to clarify what is expected of a system of axioms itself for it to be accepted as reliable. Here are two basic requirements:
Consistency
: Mathematical inferences from the use of axioms should not result in contradictions; in other words, mathematical conclusions deriving from the axioms should not contradict each other.
Completeness
: Every mathematical claim about the system that the axioms describe can be proven or disproven by using the axioms themselves.
The consistency requirement is self-evident. In many day-to-day events the human reaction to an encounter with logical contradictions is not one of great upheaval because we are constantly exposed to situations that we do not examine in depth or even to apparent contradictions that we are prepared to accept as part of our daily lives. Mathematics, however, cannot allow itself internal contradictions. That is, a mathematical system cannot allow a conclusion that is both true and untrue.
The completeness requirement is more intricate. The basic idea is that when we formulate a hypothesis, let us say about numbers, the system of axioms that describes the numbers must be rich enough for us to be able to decide whether the hypothesis is or is not correct within the system of axioms. If that is not so, there could be, say, number systems that contradict each other that satisfy the system of axioms and we will not know which is correct and which is not. This does not mean that a system that is incomplete is useless. The completeness property, however, ensures that in principle we can conclude whether a claim is correct without having to resort to additional axioms.
When the Zermelo-Fraenkel system of axioms was formulated and the first successful steps were taken to corroborate its consistency and completeness, the mathematics community was spiritually uplifted. The axioms seemed reasonable and were formulated meticulously. Although their consistency and completeness have not been completely proven, the intuition and care with which the axioms were constructed appears flawless, and the first steps to establish their consistency and completeness are promising. Hilbert himself published the grand program: a full formulation of the system of axioms for mathematics that would be consistent and complete. He declared in a lecture in 1930 on the occasion of his retirement
We have to know, and we will know.
And that is what is inscribed, in German, on his tombstone.
61. ANOTHER MAJOR CRISIS
The “evil” came from Austria. Kurt Gödel was born in Brünn (now Brno), then a Czech town in the Austro-Hungarian Empire. When that empire broke up, Gödel automatically became a Czech citizen, but he considered himself Austrian and studied at the University of Vienna. There he completed his doctorate studies and two years later, in 1931, published his famous incompleteness theorem, which we will describe below. While
in Vienna, when the Nazis came to power in Germany, he was severely affected by the brutality and anti-Semitism of Nazi groups in Austria and by the murder of Moritz Schlick on the steps of the university. Schlick was a member of the university's academic staff and of the logical-philosophical Vienna Circle, of which Gödel was also a member. Although Gödel was not Jewish, he became paranoiac and remained so all his life. In the 1930s Gödel received several invitations to go to the United States, and he stayed at the Institute for Advanced Study in Princeton, alongside Einstein, who became a close friend. Gödel's yearnings for Vienna grew stronger, and despite his fears he returned to Austria. He was in Vienna in the beginning of the war as a German citizen, citizenship he had received with the German annexation of Austria. But the pressure grew and in 1940 he moved back to the United States, accepting an invitation to become a permanent member of the Institute for Advanced Study in Princeton, where he remained until his death in 1978.
Gödel's interest in the foundations of mathematics and the link between logic and the developing set theory began in the time of his doctoral studies. His doctoral thesis presented a result that merged well with the program that Hilbert envisioned. Gödel proved that with a consistent and finite list of axioms, if every system that fulfilled the axioms had a certain property, it could be proven from the axioms themselves. This was a promising step forward. What was now needed to complete Hilbert's program was “only” to prove that the Zermelo-Fraenkel system was consistent and that every property of a system that satisfies the axioms exists in every system that satisfies the axioms. Two years later, however, Gödel himself presented a result that completely negated Hilbert's program, and that was
Gödel's incompleteness theorem
.
The theorem showed that in every finite system of axioms (or even infinite system, if it was created by algorithmic computation) that is rich enough to include the natural numbers, there will always be theorems that cannot be proven or disproven. In other words, such a system cannot be complete!
This result was a slap in the face for all those, like Hilbert, who believed that there is nothing in mathematics that we cannot know; in other words,
those who believed that the logical approach based on axioms that can be stated clearly will always result in the resolution of the question whether a particular mathematical claim is correct or not. Gödel's result also relates to systems such as the system of natural numbers constructed by Peano, the system of types developed by Whitehead and Russell, and the system of axioms of Zermelo and Fraenkel. With regard to such systems of axioms he showed that it is impossible to prove that the system does not have contradictions by using the axioms themselves. That is, if we rely only on the axioms of the system, then either one day we will discover a contradiction, or we will never know whether the system contains a contradiction. (It may be possible to prove consistency by using a broader theory, but such a theory has not yet been discovered.) The inconsistency theorem did not affect the intuitionist approach, but neither did it breathe renewed life into it. There is a strong desire to operate in an environment without potential contradictions, but not at the price of significantly limiting the range within which mathematics can develop.
Beyond the philosophical aspect and the questions relating to the foundations of mathematics, Gödel's result had a direct effect on the practice of research in mathematics. Throughout the development of mathematics, when a mathematician set out to prove a theorem, he faced two possibilities. One was that the theorem was correct, and he had to find a proof. The other was the theorem was not correct, and he had to disprove it, either by bringing a counterexample or by finding a contradiction between the theorem and other results. The incompleteness theorem gives rise to a third possibility, that the theorem cannot be proven or disproven.
Let us take as an example Fermat's last theorem, which states that for any four natural numbers
X
,
Y
,
Z
and
n
, if
n
is greater than 2, the sum
X
n
+
Y
n
cannot equal
Z
n
. For more than three hundred years, mathematicians tried to prove or disprove the theorem. With the publication of Gödel's incompleteness theorem a third possibility was added: Fermat's theorem could be one of those that cannot be proven or disproven. In 1995 Andrew Wiles published a proof of the theorem, and the cloud of incompleteness around Fermat's theorem was dispelled.
Goldbach's conjecture, formulated by Christian Goldbach in 1742, is also simple: Every even number is the sum of two prime numbers. Despite the simplicity of the formulation, still today no one has proven or disproven the conjecture, and here too nobody knows whether it is one of the theorems that Gödel's theorem applies to.
Now for a third hypothesis, Georg Cantor's continuum hypothesis, that is, the question referred to in section 59: Does C =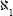 ? Cantor invested much effort in trying to prove or disprove this claim, using the naive approach to set theory, the approach in which Russell found the contradiction. Following the formulation of the Zermelo-Fraenkel axioms, the question became: Is the equality C =
? Cantor invested much effort in trying to prove or disprove this claim, using the naive approach to set theory, the approach in which Russell found the contradiction. Following the formulation of the Zermelo-Fraenkel axioms, the question became: Is the equality C =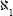 correct or incorrect in the context of those axioms?
correct or incorrect in the context of those axioms?