The Amazing Story of Quantum Mechanics (34 page)
Read The Amazing Story of Quantum Mechanics Online
Authors: James Kakalios
What determines the current observed in a metal for a given applied voltage? Normally the electrons can surf using the atoms in the metal wire—as long as the atoms are in a uniform crystalline arrangement, they do not impede the electrical current. One can run on a city sidewalk and never step on a crack (thereby preserving one’s mother’s back) as long as the placement of the concrete segments is uniform and matched to one’s stride. If there is a hole in the sidewalk, or a protruding tree root, or a shortened segment, then it is likely that the runner will stumble. In any real metal wire there will be defects such as crystalline imperfections (atoms randomly located out of their preferred ordered positions) and impurities that inevitably sneak into the solid during the fabrication process. Electrons accelerated by a voltage will scatter from these defects and transfer some of their kinetic energy to these atoms.
Sometimes this scattering is a good thing, as in an incandescent lightbulb or a toaster. There a large current is forced through a narrow filament, and the accelerated electrons transfer so much of their energy to the atoms in the wire that they shake violently about their normal crystalline positions. This shaking heats the wire until it is glowing red-hot (as in the coils in your toaster), and for higher currents in thinner wires, the shaking can cause excitation of electrons to all higher energy states equally, with resultant emission of light of all frequencies, perceived as white light (as in the filament of a lightbulb). Sometimes the loss of energy through collisions with atoms in the metallic wire is a bad thing, as in electrical power transmission cables; in order to compensate for these energy losses, the voltages along the lines must be very high, requiring power substations and transformers along the line.
Computer hard-drive disc readers employ the scattering of an electrical current by magnetic atoms to sense the different fields of the magnetized bits. A thin, nonmagnetic metal is sandwiched between two magnetic metals. In the absence of an external magnetic field, one slice of magnetic “bread” is permanently polarized so that its magnetic field points in one direction within the layer, while the other slice of bread is polarized in another direction (the nature of the quantum mechanical coupling between the magnetic layers, separated by the nonmagnetic middle layer, leads to this configuration being the low-energy state).
Imagine a flow of electrons perpendicular through the top of this “sandwich,” passing through the face of one slice of magnetic bread, through the nonmagnetic metal meat of the sandwich, and finally through the face of the other magnetic metal bread slice, as shown in Figure 47. When first entering the first magnetized layer, the electrons are unpolarized—their internal magnetic fields are as likely to point in one direction (spin “up”) as the other (spin “down”). The first ferromagnetic layer polarizes the electrons, and those that move into the nonmagnetic spacer layer will have their internal magnetic fields pointing in the same direction as the field in the first metal layer. When they reach the second magnetized layer, which normally has a field pointing in the opposite direction, these polarized electrons are mostly reflected, so very little electrical current passes through the second layer and leaves the sandwich. If very little current results for a given voltage, we say that the device has a high resistance for an electrical current passing perpendicular through the three layers.
Now this structure is placed in an external magnetic field, such as that created by a magnetized bit on a computer hard drive. The external field forces both magnetic layers in this sandwich (Figure 47b) to point in the same direction. When an electrical current now passes through this structure, the first layer polarizes the electron’s magnetic fields as before, and the second layer, now pointing in the same direction, readily allows the electrons to pass through, and hence a large current flows through the three-layer device. This change in resistance with an external magnetic field can be very large, up to 80 percent or more (they are, seriously, technically known as giant magnetoresistance devices), which means that they are very sensitive to even small magnetic fields. One can thus make the magnetically polarized bits on the hard drive smaller and still be able to reliably read out the sequence of “ones” and “zeros.” Smaller bits means more of them can be packed on a given disc area, and the storage capabilities of computer hard drives have increased dramatically since the introduction of this first spintronic device.
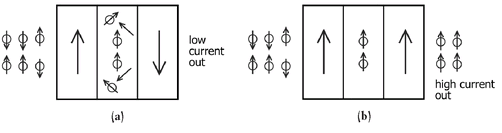
Figure 47:
Sketch of the device structure used to measure magnetic fields with an electrical current in a computer hard drive. An electrical current has both a negative charge and a built-in magnetic field resulting from its quantum mechanical intrinsic angular momentum (“spin”). Electrons flowing into the device are magnetically polarized by the first layer. In (a), the second layer is aligned opposite to the first, so the electrons polarized by the first layer are repelled by the second, and a very small current results. In the second case (b), the second magnetic layer is aligned in the same direction as the first, and the polarized electrons easily pass through the second layer. This configuration would present a low resistance to the flow of current, while the first case (a) would represent a high resistance state.
Sketch of the device structure used to measure magnetic fields with an electrical current in a computer hard drive. An electrical current has both a negative charge and a built-in magnetic field resulting from its quantum mechanical intrinsic angular momentum (“spin”). Electrons flowing into the device are magnetically polarized by the first layer. In (a), the second layer is aligned opposite to the first, so the electrons polarized by the first layer are repelled by the second, and a very small current results. In the second case (b), the second magnetic layer is aligned in the same direction as the first, and the polarized electrons easily pass through the second layer. This configuration would present a low resistance to the flow of current, while the first case (a) would represent a high resistance state.
The first generation of iPods was able to store large data files on a small magnetic disc because the sensors used to read the information made use of the giant magnetoresistance effect. The drive to pack smaller magnetic bits at higher densities has led to the development of magnetic sensors on hard drives that employ another quantum mechanical phenomenon—tunneling—to sense the magnetic fields of the bits. These sensors have essentially the same structure as the device in Figure 47. Instead of a nonmagnetic metal placed between the two magnetic slices of bread, a thin insulator is used. A current can pass through the device only via tunneling, and the probability of this process turns out to be very sensitive to the magnetic polarization on either side of the barrier. These devices provide an even more sensitive probe of very small magnetic fields and are found in computer hard drives currently available for purchase. Every time we access information on our computers, we are making use of the practical applications of quantum mechanical tunneling.
The basic principles underlying giant magnetoresistance are finding new applications in future spintronic devices. Giant magnetoresistance was discovered in 1988 by Albert Fert in France and independently by Peter Grünberg in Germany, for which they shared the Nobel Prize in Physics in 2007. By 1997, hard drives containing read heads using the giant magnetoresistance effect were available for sale. It is actually not unusual for quantum-mechanics-enabled devices to quickly find their way into consumer products. Bell Labs held a press conference announcing the invention of the transistor in 1948, and by 1954 one could purchase the first (expensive) transistor radio.
CHAPTER NINETEEN
A Window on Inner Space
In the 1963 Roger Corman
science fiction film
X: The Man with the X-ray Eyes,
Dr. James Xavier, searching for improvements in patient care, develops a serum in the form of eye drops that enables a person to see through solid matter. Eschewing animal testing as not being suitably reliable, he experiments on himself and does indeed gain the ability to see through a person’s clothing and epidermis. However, this success leads to one of the greatest catastrophes that can befall any scientist—he loses his research grant when his funding agency discounts his claims of “X-ray vision!” Nevertheless, his ability to see within the interior of a person enables him to save a small child’s life, as he recognizes that she was about to receive an unnecessary and ineffective operation. Sadly for Dr. Xavier, his X-ray vision becomes stronger and stronger, until his eyelids and thick dark glasses provide no respite. It does not end well for the well-meaning doctor, as the biblical expression “If thine eye offend thee ...” plays a key role in the film’s conclusion.
science fiction film
X: The Man with the X-ray Eyes,
Dr. James Xavier, searching for improvements in patient care, develops a serum in the form of eye drops that enables a person to see through solid matter. Eschewing animal testing as not being suitably reliable, he experiments on himself and does indeed gain the ability to see through a person’s clothing and epidermis. However, this success leads to one of the greatest catastrophes that can befall any scientist—he loses his research grant when his funding agency discounts his claims of “X-ray vision!” Nevertheless, his ability to see within the interior of a person enables him to save a small child’s life, as he recognizes that she was about to receive an unnecessary and ineffective operation. Sadly for Dr. Xavier, his X-ray vision becomes stronger and stronger, until his eyelids and thick dark glasses provide no respite. It does not end well for the well-meaning doctor, as the biblical expression “If thine eye offend thee ...” plays a key role in the film’s conclusion.
Fortunately we can safely peer inside a person, see his or her internal organs, and discriminate healthy tissue from cancerous growths, without the disastrous consequences suffered by Dr. Xavier. I now address a device that has become common in most hospitals and many medical clinics and would certainly have strained the credulity of the editors of any science fiction pulp magazine had it been featured in a submitted story—magnetic resonance imaging, or MRI. This process, enabling detailed high-resolution imaging of the interior of a person, is a striking illustration of how our understanding of the quantum nature of matter, driven by scientists’ curiosity in the 1920s and 1930s about the rules governing the behavior of atoms and light, has led to the development of technologies that futurists could not suspect fifty years ago.
We have made use of the intrinsic angular momentum of fundamental subatomic particles when determining which form of quantum statistics—Fermi-Dirac or Bose-Einstein—they would obey. In this way the internal spin is crucial to understanding the nature of metallic or insulating solids but was not employed directly when describing the physics of diodes or transistors. Associated with the spin is a small intrinsic magnetic field that enabled Stern and Gerlach to measure the spin in the first place (Chapter 4), and remotely probing the magnetic field from the spin of nuclear protons enables magnetic imaging.
We are composed mostly of water—molecules consisting of an oxygen atom bound to two hydrogen atoms. Each hydrogen atom has a single proton in its nucleus. The intrinsic spin of the proton is ±ℏ/2, and there is a small magnetic field associated with each proton. The magnetic field has a north and south pole (Chapter 4, Figure 10), and when we place the water molecule in an external magnetic field, the hydrogen atom’s proton points either in the same direction as the applied field (that is, its north pole points up while the lab magnetic field does likewise) or in the opposite direction (its north pole points down while the external field’s north pole points up). The proton in the nucleus has a series of available quantum levels, just as the electron has its own series of possible states. If the proton’s magnetic field is in the same direction as the external magnetic field, it is in a lower energy state. If the proton’s magnet is opposite to the external magnetic field, then it will have a higher energy, as it takes work to rotate it to the lower-energy, aligned configuration. As indicated in Figure 48, the energy level that is occupied by the single proton can thus be split into two energy values by placing the hydrogen atom between the poles of a strong magnet, with the proton’s energy being lower than what we find with no outside field or the energy being higher, depending on whether the proton’s magnetic field points with or against the external field, respectively.
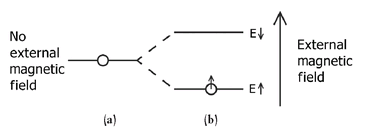
Figure 48:
Sketch of the energy level of a single proton in the nucleus of a hydrogen atom (a) when no outside magnetic field is applied and (b) when a field is present. In the second case the proton’s energy is lowered if its own intrinsic magnetic field points in the same direction as the outside magnet, and the energy is higher if it points in an opposite direction. In this figure the proton is indicated with its spin aligned with the external magnetic field and thus in the lower energy state. If the spin were opposite to the external field, the proton would reside in the higher energy state.
Sketch of the energy level of a single proton in the nucleus of a hydrogen atom (a) when no outside magnetic field is applied and (b) when a field is present. In the second case the proton’s energy is lowered if its own intrinsic magnetic field points in the same direction as the outside magnet, and the energy is higher if it points in an opposite direction. In this figure the proton is indicated with its spin aligned with the external magnetic field and thus in the lower energy state. If the spin were opposite to the external field, the proton would reside in the higher energy state.
Say a proton is aligned in the same direction as the external magnetic field, in the lower-energy split state (Figure 48b). If I provide energy, in the form of a photon, I can promote the proton to the higher-energy state, which corresponds to the proton’s magnetic field being opposite to the outside magnet. This resonant absorption is entirely analogous to the line spectra (Chapter 5, Figure 13) for electronic energy levels in an atom. In essence the photon provides energy to flip the proton’s internal magnet, from pointing up to pointing down (for example). It is as if I had a top that was spinning clockwise, and with an appropriate pulse of energy I caused its direction to reverse, so that it was now rotating counterclockwise.
Other books
The Gravity Engine by Kylie Chan
Will Power by A. J. Hartley
Love Songs by Bernadette Marie
The Lost Island by Douglas Preston
Silent Girl by Tricia Dower
Out on Blue Six by Ian McDonald
Against the Gods: The Remarkable Story of Risk by Peter L. Bernstein
The Death and Life of Superman by Roger Stern
The Blonde Theory by Kristin Harmel