Understanding Sabermetrics (4 page)

Read Understanding Sabermetrics Online

Authors: Gabriel B. Costa,Michael R. Huber,John T. Saccoma

Before we move on, however, there are many other factors which must be addressed. In Ruth’s case, some of these include the fact that he did not play night games, that he never traveled by airplane on road trips and that he did not play against African-American opponents. These issues will be considered later on in the chapter Seventh Inning Stretch: Non-Sabermetrical Factors.
The Sultan of Swat held the career-home-run title from 1921 until 1974. The example above demonstrates how Babe Ruth’s home run prowess can be sabermetrically reasoned to argue his dominance. Let’s look at a pitching example. Suppose we wish to make an argument about the “magic number” of wins which will ensure a starting pitcher’s election into Baseball’s Hall of Fame. For decades, baseball players, writers, and fans would argue that 300 wins translates to a “lock” for admittance into Cooperstown. With most teams now employing a five-man starting rotation, is it possible any longer for a pitcher to win 300 games in his career? Let’s establish a sabermetrical reasoning argument, according to our algorithm.
First, identify the question. “What is the career pitching victory total that should guarantee election for a pitcher into the Hall of Fame?” Maybe it will stay at 300 wins, but maybe not. Next, gather all the relevant information. Going to the World Wide Web, we need to gather information on those starting pitchers currently in the Hall and their victory totals. We also need to gather information on current (active) starting pitchers and seek to develop any trends, using as many measures as possible. Confining our search to starting pitchers, we find that there are 70 pitchers with a plaque in the Hall of Fame. Twenty-two of these have 300 or more career victories. Interestingly, all retired pitchers with at least 300 career victories are in the Hall of Fame (Greg Maddux is still active). Further, Bobby Mathews, who played 15 seasons from 1871 to 1887, ended his career with 297 victories, and he was
not
voted into the Hall of Fame.
What other measures or instruments should be introduced? Should we consider the average number of starts per season (for starters)? Cy Young pitched 22 years for the Cleveland Spiders (NL), St. Louis Cardinals (NL), Boston Americans (then Red Sox) (AL), and Cleveland Indians (AL), totaling 815 games started. His career total of 511 wins (and 316 losses) will probably never be equaled. In those 22 seasons, the Cyclone averaged just over 37 starts per season (even when 40 years old). He also averaged just over 23 wins per season. Walter “Big Train” Johnson is second on the all-time list with 417 career victories, all for the Washington Senators. In 21 seasons, he averaged close to 32 starts and almost 20 wins each season. One of the greatest left-handed starting pitchers of all time was Warren Spahn, who pitched for the Boston (and then Milwaukee) Braves. Spahnny had one fewer career start than the Big Train but garnered “only” 363 victories. One reason for this might be that he didn’t begin really playing major league baseball until the age of 25, due to service in World War II. Over 21 seasons, he averaged just over 17 wins and 31 starts per season. Our sabermetrical reasoning should continue for every pitcher in the Hall of Fame. By examining the average number of starts and wins in a season, we can introduce some normalization into the study. By comparing these to other pitchers of their eras, or comparing their statistics to league averages, we could introduce the idea of relativity into the study. We could also explore the statistic of winning percentage (total wins divided by wins plus losses) or the notion of average wins per start. Cy Young had 511 wins / 815 starts = 0.627 wins per start. Or, looking at the reciprocal, Cy Young won a game every 1.59 starts (which really means that he won nearly two games every three games he started).
Roger Clemens, in comparison, had 354 victories at the end of the 2007 season, together with 707 career games started (he had one relief appearance during his 1984 rookie season). In 23 years, this translates to an average of 30 starts per season and just over 15 wins per season. If we multiply Clemens’s average wins per start (0.500) times 49 starts, which is what Cy Young had in 1892 for the Spiders, we see that Clemens would win 24.5 games. Clemens has broken the 20-win plateau six times, with a career high of 24 in his third season, 1986. This is the point where we need to exercise caution with respect to extrapolation and prediction. Clemens never started more than 36 games in any of his 24 seasons. Why would we expect him to start 49 games, as Young did?
Now we look at the population of current starting pitchers. To get an unbiased population, we need to select those pitchers with a baseline of career starts or career victories, perhaps 100, 150, or 200. We do not want to be too restrictive. Next, interpret the results. Randy “Big Unit” Johnson had won 284 games in his 20-year career through the end of the 2007 season. He had also won five Cy Young Awards (and placed second three more times) as the best pitcher in his league. We can easily compute his average wins per season. Should his victory total be enough for the Hall of Fame? As a final example, consider the career of Greg “Mad Dog” Maddux. An amazing eighteen times in his 22-year career (through the 2007 season), Maddux won at least fifteen games in the season. That got him to the magic number of 300, and he has added to it every year, with 347 total victories. Perhaps we could determine how many other current pitchers have won at least fifteen games per season and could do it for 20 years (15 times 20 equals 300).
Here is where the historical context comes into play. Also, we might realize that our sabermetrical reasoning has some limitations. Perhaps non-sabermetrical factors now play a part. If you were voting for admittance into the Hall of Fame, how much weight would you put on a pitcher who pitched in fifteen All-Star games? With the recent role shifting of pitchers (“starters” give way to “set-up men” who then turn the game over to “closers”), and the fact that starting pitchers are currently averaging fewer innings per start than in earlier decades (which means close games might be decided after the starter has departed the game), our original question is not as trivial as initially suspected. If you can develop a sabermetrical argument that creates a new magic number of wins, several pitchers (and their agents) will suddenly be your best friends, while others will blame you for not getting a ticket to Cooperstown.
Fast Ball Down the Middle
 
Regarding home runs, has anyone in history been either as dominant or more dominant than Babe Ruth?
Curve Ball Low and Away
 
Who was the more dominant pitcher, Cy Young or Nolan Ryan? Consider both sabermetrical and non-sabermetrical factors.
Inning 1: Simple Additive Formulas
 
While many sabermetrical formulas are rather complicated mathematical models, there are some that are very simple to compute, and can be used to compare players of different skills on a level playing field, i.e., they do not favor the high average hitter over the slugger, or vice versa. This first statistic, however, definitely favors the big power hitter.
On Base Plus Slugging and Batting Average (OPS + BA)
 
Most people are aware of OPS (see “Batting Practice” section) as a measure of offensive effectiveness, but the creator or creators of the POP
™
Award (
http://www.popaward.com/htdocs/index.htm
) have come up with an extension of the formula to include batting average, calling it POP, which accumulates OPS and BA. Thus, if a player has a batting average of .300, an on-base percentage of .400, and a slugging percentage of .500, he would have POP = BA + OBA + SLG = .300 + .400 + .500 = 1.200. According to the POP
™
Award Web site, 48 percent of the players who achieve one such season are enshrined in the Hall of Fame, and 71 percent of those with two or more such seasons, called “premier” seasons, are so honored.
In 1966, when he won the American League Most Valuable Player award while playing for the Baltimore Orioles, Frank Robinson had BA = .316, OBP = .410, and SLG = .637, so his POP was the sum of those figures — 1.363, one of five “premier” seasons in which he would have BA greater than .300, OBP greater than .400, and SLG greater than .500.
In 1954, when he was named National League Most Valuable Player while playing for the New York Giants, Willie Mays had a POP of 1.423, with BA = .345, OBP = .411, and SLG = .667, one of his four “premier” seasons.
HEQ-Offense
 
Michael Hoban was a professor of mathematics and dean at Monmouth University in New Jersey. He defined a formula to measure a batter’s effectiveness, called the Hoban Effectiveness Quotient (HEQ): TB + R + RBI + SB + 0.5 × BB. Hoban stated that an HEQ of 600 represents an outstanding year at the bat. When evaluating players’ careers, he looked at the average of the players’ 10 best seasons of HEQ. In this way, he was measuring the consistency of a player’s level of achievement over time.
The beauty of the formula lies in its simplicity; it is measure of how much business a player transacted in a given season. When he stole a record 130 bases in a single season (1982), Oakland outfielder Rickey Henderson scored an HEQ of 563. In that season, Henderson batted .267 and had an OPS of .780. The following table lists Henderson’s offensive statistics:
 
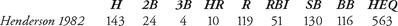
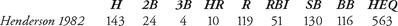
Table 3.1 Rickey Henderson’s HEQ for 1982
 
To calculate his HEQ, we first need to determine Henderson’s total bases (TB). The standard method of computing TB requires separating out the singles. Henderson had 143 hits. When we subtract the total number of non-singles from his hits (24 + 4 + 10 = 38), we get 143 − 38 = 105 singles. Thus, using the formula TB = Singles + (2 × Doubles) + (3 × Triples) + (4 × Home Runs), we obtain 105 + 2(24) + 3(4) + 4(10) = 205 total bases. This allows us to calculate Henderson’s HEQ = TB + R + RBI + SB + 0.5 × BB = 205 + 119 + 51 + 130 + 0.5 × 116 = 563.
There is a shortcut that can be employed as well in the calculation of TB. Since the total number of hits is redundant in the double, triple and home run totals, TB can be calculated by reducing the weights on each of these figures by 1, and then adding the number of hits. Thus, instead of having a weight of 2, the doubles total is multiplied by 1, triples by 2 and home runs by 3: TB = H + Doubles + (2 × Triples) + (3 × Home Runs) = 143 + 24 + 2(4) + 3(10), which also equals 205.
During the same season, Milwaukee outfielder Gorman Thomas, co-HR champion, batted .245 with an OPS of .849. His HEQ was 540 (verifiable using the fact that his total bases were 287). Thomas’s statistics for 1982 are listed in the following table:
 
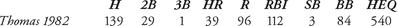
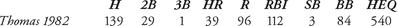
Table 3.2 Gorman Thomas’ HEQ for 1982
 
A statistic such as HEQ can put players like Thomas and Henderson on a more or less equal footing as a basis of comparison, even though their skill sets were vastly different in 1982 (home run slugger versus all-time base stealer). HEQ is not recommended as a measure to compare players from different seasons.
There also is a defensive component for the HEQ, so from here on in, the offensive HEQ will be denoted HEQ-O, and the defensive component will be denoted HEQ-D.
HEQ-Defense
 
The defensive formula for HEQ is a bit more complicated, but it still is relatively easy to use. The fact is that, despite the disfavor into which fielding percentage has fallen among baseball researchers, there are not many ways to quantify defense.
Just like the HEQ-O formula, HEQ-D reflects the quantity of positive defensive plays. It is constructed as a different weighted formula for each defensive position, and the only raw data required is PO (putouts), A (assists), E (errors) and DP (double plays). All of these statistics are weighted, and each position has a Position Multiplication Factor (PMF) that adjusts the numbers in such a way that a season of 400 is considered outstanding. Pitchers are not measured using this statistic. Here are the HEQ-D formulas by position:
 

Other books

Tessa's Redemption by Josie Dennis
Darkness Devours by Keri Arthur
He's Her by Mimi Barbour
B00AFYX78I EBOK by Harrison, Kate
Finding Mr. Right Now by Meg Benjamin
The Two Faces of January by Patricia Highsmith
Hot Pursuit by Gemma Fox