Data Mining (21 page)
Authors: Mehmed Kantardzic
and finally, if all the values in a bin are replaced by the closest of the boundary values, the new set will be
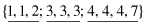

One of the main problems of this method is to find the best cutoffs for bins. In theory, a decision about cutoffs cannot be made independently of other features. Still, heuristic decisions for every feature independently give good results in many data-mining applications. The value-reduction problem can be stated as an optimization problem in the selection of k bins. Given the number of k bins, distribute the values in the bins to minimize the average distance of a value from its bin mean or median. The distance is usually measured as the squared distance for a bin mean and as the absolute distance for a bin median. This algorithm can be computationally very complex, and a modified heuristic procedure is used to produce a near-optimum solution. The procedure consists of the following steps:
1.
Sort all values for a given feature.
2.
Assign approximately equal numbers of sorted adjacent values (v
i)
to each bin, where the number of bins is given in advance.
3.
Move a border element v
i
from one bin to the next (or previous) when that reduces the global distance error (ER; the sum of all distances from each v
i
to the mean or mode of its assigned bin).
A simple example of the dynamic bin procedure for feature discretization is given next. The set of values for a feature f is {5, 1, 8, 2, 2, 9, 2, 1, 8, 6}. Split them into three bins (k = 3), where the bins will be represented by their modes. The computations in the first iteration of the algorithm are
1.
Sorted set of values for feature f is {1, 1, 2, 2, 2, 5, 6, 8, 8, 9}
2.
Initial bins (k = 3) are
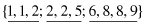
3.
(i) Modes for the three selected bins are {1, 2, 8}. After initial distribution, the total error, using absolute distance for modes, is
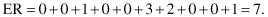
4.
(iv) After moving two elements from BIN
2
into BIN
1
and one element from BIN
3
to BIN
2
in the next three iterations and obtaining smaller and smaller ER, the new and final distribution of elements will be
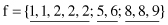

The corresponding modes are {2, 5, 8}, and the total minimized error ER is 4. Any additional move of elements between bins will cause an increase in the ER value. The final distribution, with medians as representatives, will be the solution for a given value-reduction problem.
Another very simple method of smoothing feature values is
number approximation by rounding
. Rounding is a natural operation for humans; it is also natural for a computer, and it involves very few operations. First, numbers with decimals are converted to integers prior to rounding. After rounding, the number is divided by the same constant. Formally, these steps are described with the following computations applied to the feature value X:
1.
Integer division: Y = int (X/10
k
)
2.
Rounding:
If
(mod [X,10
k
] ≥ [10
k
/2])
then
Y = Y + 1
3.
Integer multiplication: X = Y * 10
k
where k is the number of rightmost decimal places to round. For example, the number 1453 is rounded to 1450 if k = 1, rounded to 1500 if k = 2, and rounded to 1000 if k = 3.
Given a number of values for a feature as an input parameter of the procedure, this simple rounding algorithm can be applied in iterations to reduce these values in large data sets. First, a feature’s values are sorted so that the number of distinct values after rounding can be counted. Starting at k = 1, rounding is performed for all values, and the number of distinct values counted. Parameter k is increased in the next iteration until the number of values in the sorted list is reduced to less than the allowable maximum, typically in real-world applications between 50 and 100.
3.7 FEATURE DISCRETIZATION: CHIMERGE TECHNIQUE
ChiMerge is one automated discretization algorithm that analyzes the quality of multiple intervals for a given feature by using χ
2
statistics. The algorithm determines similarities between distributions of data in two adjacent intervals based on output classification of samples. If the conclusion of the χ
2
test is that the output class is independent of the feature’s intervals, then the intervals should be merged; otherwise, it indicates that the difference between intervals is statistically significant, and no merger will be performed.
ChiMerge algorithm consists of three basic steps for discretization:
1.
Sort the data for the given feature in ascending order.
2.
Define initial intervals so that every value of the feature is in a separate interval.
3.
Repeat until no χ
2
of any two adjacent intervals is less then threshold value.
After each merger, χ
2
tests for the remaining intervals are calculated, and two adjacent features with the χ
2
values are found. If the calculated χ
2
is less than the lowest threshold, merge these intervals. If no merge is possible, and the number of intervals is greater than the user-defined maximum, increase the threshold value.
The χ
2
test or the contingency table test is used in the methodology for determining the independence of two adjacent intervals. When the data are summarized in a contingency table (its form is represented in Table 3.5), the χ
2
test is given by the formula:
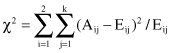
where
| k | = the number of classes, |
| A ij | = the number of instances in the i th interval, j th class, |
| E ij | = the expected frequency of A ij , which is computed as (R i C j )/N, |
| R i | = the number of instances in the i th interval = ∑ A ij , j = 1,…, k, |
| C j | = the number of instances in the j th class = ∑ A ij , i = 1,2, |
| N | = the total number of instances = ∑ R i , i = 1,2. |