Data Mining (9 page)
Authors: Mehmed Kantardzic
For example, if the initial set of values of the attribute is v = {1, 2, 3}, then
mean
(v) = 2,
sd
(v) = 1, and the new set of normalized values is v* = {−1, 0, 1}.
Why not treat normalization as an implicit part of a data-mining method? The simple answer is that normalizations are useful for several diverse methods of data mining. Also very important is that the normalization is not a one-time or a one-phase event. If a method requires normalized data, available data should be initially transformed and prepared for the selected data-mining technique, but an identical normalization must be applied in all other phases of data-mining and with all new and future data. Therefore, the normalization parameters must be saved along with a solution.
2.3.2 Data Smoothing
A numeric feature, y, may range over many distinct values, sometimes as many as the number of training cases. For many data-mining techniques, minor differences among these values are not significant and may degrade the performance of the method and the final results. They may be considered as random variations of the same underlying value. Hence, it can be advantageous sometimes to smooth the values of the variable.
Many simple smoothers can be specified that average similar measured values. For example, if the values are real numbers with several decimal places, rounding the values to the given precision could be a simple smoothing algorithm for a large number of samples, where each sample has its own real value. If the set of values for the given feature F is {0.93, 1.01, 1.001, 3.02, 2.99, 5.03, 5.01, 4.98}, then it is obvious that smoothed values will be F
smoothed
= {1.0, 1.0, 1.0, 3.0, 3.0, 5.0, 5.0, 5.0}. This simple transformation is performed without losing any quality in a data set, and, at the same time, it reduces the number of different real values for the feature to only three.
Some of these smoothing algorithms are more complex, and they are explained in Section 3.2. Reducing the number of distinct values for a feature means reducing the dimensionality of the data space at the same time. Reduced values are particularly useful for logic-based methods of data mining, as will be explained in Chapter 6. Smoothers in this case can be used to discretize continuous features into a set of features with binary true–false values.
2.3.3 Differences and Ratios
Even small changes to features can produce significant improvement in data-mining performances. The effects of relatively minor transformations of input or output features are particularly important in the specification of the data-mining goals. Two types of simple transformations,
differences
and
ratios,
could make improvements in goal specification, especially if they are applied to the output features.
These transformations sometimes produce better results than the simple, initial goal of predicting a number. In one application, for example, the objective is to move the controls for a manufacturing process to an optimal setting. But instead of optimizing the absolute magnitude specification for the output s(t + 1), it is more effective to set the goal of a relative move from current value to a final optimal s(t + 1) − s(t). The range of values for the relative moves is generally much smaller than the range of values for the absolute control setting. Therefore, for many data-mining methods, a smaller number of alternatives will improve the efficiency of the algorithm and will very often give better results.
Ratios are the second simple transformation of a target or output features. Using s(t + 1)/s(t) as the output of a data-mining process instead of absolute value s(t + 1) means that the level of increase or decrease in the values of a feature may also improve the performances of the entire mining process.
Differences and ratio transformations are not only useful for output features but also for inputs. They can be used as changes in time for one feature or as a composition of different input features. For example, in many medical data sets, there are two features of a patient (height and weight) that are taken as input parameters for different diagnostic analyses. Many applications show that better diagnostic results are obtained when an initial transformation is performed using a new feature called the body mass index (BMI), which is the weighted ratio between weight and height. This composite feature is better than the initial parameters to describe some of the characteristics of the patient, such as whether or not the patient is overweight.
Logical transformations can also be used to compose new features. For example, sometimes it is useful to generate a new feature that will determine the logical value of the relation A > B between existing features A and B. But there are no universally best data-transformation methods. The lesson to be learned is that a major role remains for human insight while defining the problem. Attention should be paid to composing features, because relatively simple transformations can sometimes be far more effective for the final performance than switching to some other techniques of data mining.
2.4 MISSING DATA
For many real-world applications of data mining, even when there are huge amounts of data, the subset of cases with complete data may be relatively small. Available samples and also future cases may have values missing. Some of the data-mining methods accept missing values and satisfactorily process data to reach a final conclusion. Other methods require that all values be available. An obvious question is whether these missing values can be filled in during data preparation, prior to the application of the data-mining methods. The simplest solution for this problem is the reduction of the data set and the elimination of all samples with missing values. That is possible when large data sets are available, and missing values occur only in a small percentage of samples. If we do not drop the samples with missing values, then we have to find values for them. What are the practical solutions?
First, a data miner, together with the domain expert, can manually examine samples that have no values and enter a reasonable, probable, or expected value, based on a domain experience. The method is straightforward for small numbers of missing values and relatively small data sets. But, if there is no obvious or plausible value for each case, the miner is introducing noise into the data set by manually generating a value.
The second approach gives an even simpler solution for elimination of missing values. It is based on a formal, often automatic replacement of missing values with some constants, such as:
1.
replace all missing values with a single global constant (a selection of a global constant is highly application dependent);
2.
replace a missing value with its feature mean; and
3.
replace a missing value with its feature mean for the given class (this approach is possible only for classification problems where samples are classified in advance).
These simple solutions are tempting. Their main flaw is that the substituted value is not the correct value. By replacing the missing value with a constant or changing the values for a few different features, the data are biased. The replaced value (values) will homogenize the cases with missing values into a uniform subset directed toward the class with the most missing values (an artificial class). If missing values are replaced with a single global constant for all features, an unknown value may be implicitly made into a positive factor that is not objectively justified.
One possible interpretation of missing values is that they are “don’t care” values. In other words, we suppose that these values do not have any influence on the final data-mining results. In that case, a sample with the missing value may be extended to the set of artificial samples, where, for each new sample, the missing value is replaced with one of the possible feature values of a given domain. Although this interpretation may look more natural, the problem with this approach is the combinatorial explosion of artificial samples. For example, if one 3-D sample X is given as X = {1, ?, 3}, where the second feature’s value is missing, the process will generate five artificial samples for the feature domain [0, 1, 2, 3, 4]
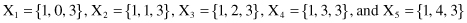
Finally, the data miner can generate a predictive model to predict each of the missing values. For example, if three features A, B, and C are given for each sample, then based on samples that have all three values as a training set, the data miner can generate a model of correlation between features. Different techniques, such as regression, Bayesian formalism, clustering, or decision-tree induction, may be used depending on data types (all these techniques are explained later in Chapters 5, 6, and 7). Once you have a trained model, you can present a new sample that has a value missing and generate a “predictive” value. For example, if values for features A and B are given, the model generates the value for the feature C. If a missing value is highly correlated with the other known features, this process will generate the best value for that feature. Of course, if you can always predict a missing value with certainty, this means that the feature is redundant in the data set and not necessary in further data-mining analyses. In real-world applications, you should expect an imperfect correlation between the feature with the missing value and other features. Therefore, all automatic methods fill in values that may not be correct. Such automatic methods are among the most popular in the data-mining community. In comparison to the other methods, they use the most information from the present data to predict missing values.
In general, it is speculative and often misleading to replace missing values using a simple, artificial schema of data preparation. It is best to generate multiple solutions of data mining with and without features that have missing values and then analyze and interpret them.
2.5 TIME-DEPENDENT DATA
Practical data-mining applications will range from those having strong time-dependent relationships to those with loose or no time relationships. Real-world problems with time dependencies require special preparation and transformation of data, which are, in many cases, critical for successful data mining. We will start with the simplest case—a single feature measured over time. This feature has a series of values over fixed time units. For example, a temperature reading could be measured every hour, or the sales of a product could be recorded every day. This is the classical univariate time-series problem, where it is expected that the value of the variable X at a given time can be related to previous values. Because the time series is measured at fixed units of time, the series of values can be expressed as
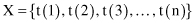
where t(n) is the most recent value.
For many time-series problems, the goal is to forecast t(n + 1) from previous values of the feature, where these values are directly related to the predicted value. One of the most important steps in the preprocessing of raw, time-dependent data is the specification of a window or a time lag. This is the number of previous values that influence the prediction. Every window represents one sample of data for further analysis. For example, if the time series consists of the 11 measurements
