Data Mining (25 page)

Before further formalization of a learning process, it is necessary to make a clear distinction between two concepts that are highly connected with a learning process. Let us discuss the differences between
statistical dependency and causality.
The statistical dependency between input X and output Y is expressed with the approximating functions of the learning method. The main point is that causality cannot be inferred from data analysis alone and concluded with some inductive, learned model using input–output approximating functions, Y = f(X, w); instead, it must be assumed or demonstrated by arguments outside the results of inductive-learning analysis. For example, it is well known that people in Florida are on average older than in the rest of the United States. This observation may be supported by inductive-learning dependencies, but it does not imply, however, that the climate in Florida causes people to live longer. The cause is totally different; people just move there when they retire and that is possibly the cause, and maybe not the only one, of people being older in Florida than elsewhere. Similar misinterpretation could be based on the data analysis of life expectancy for a married versus a single man. Statistics show that the married man lives longer than the single man. But do not hurry with sensational causality and conclusions: that marriage is good for one’s health and increases life expectancy. It can be argued that males with physical problems and/or socially deviant patterns of behavior are less likely to get married, and this could be one of possible explanations why married men live longer. Unobservable factors such as a person’s health and social behavior are more likely the cause of changed life expectancy, and not the observed variable, marriage status. These illustrations should lead us to understand that inductive-learning processes build the model of dependencies but they should not automatically be interpreted as causality relations. Only experts in the domain where the data are collected may suggest additional, deeper semantics of discovered dependencies.

Let us return again to the learning machine and its task of system modeling. The problem encountered by the learning machine is to select a function from the set of functions this machine supports, which best approximates the system’s responses. The learning machine is limited to observing a finite number of samples
n
in order to make this selection. The finite number of samples, which we call a training data set, is denoted by (X
_i
, y
_i
), where i = 1, … , n. The quality of an approximation produced by the learning machine is measured by the
loss function
L(y, f[X, w]), where

• y is the output produced by the system,
  
• X is a set of inputs,
  
• f(X, w) is the output produced by the learning machine for a selected approximating function, and
  
• w is the set of parameters in the approximating functions.
  

L measures the difference between the outputs produced by the system y
_i
and that produced by the learning machine f(X
_i
,w) for every input point X
_i
. By convention, the loss function is nonnegative, so that large positive values correspond to poor approximation, and small positive values close to 0 show a good approximation. The expected value of the loss is called the
risk functional
R(w)

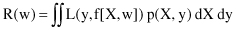
where L(y, f[X, w])is a loss function and p(X, y) is a probability distribution of samples. The R(w) value, for a selected approximating functions, is dependent only on a set of parameters w. Inductive learning can be now defined as the process of estimating the function f(X,w
_opt
), which minimizes the risk functional R(w) over the set of functions supported by the learning machine, using only the training data set, and not knowing the probability distribution p(X, y). With finite data, we cannot expect to find f(X, w
_opt
) exactly, so we denote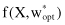
as the estimate of parameters
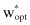of the optimal solution w
_opt
obtained with finite training data using some learning procedure.

For common learning problems such as classification or regression, the nature of the loss function and the interpretation of risk functional are different. In a two-class classification problem, where the output of the system takes on only two symbolic values, y = {0, 1}, corresponding to the two classes, a commonly used loss function measures the classification error.

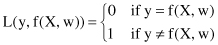
Using this loss function, the risk functional quantifies the
probability of misclassification
. Inductive learning becomes a problem of finding the classifier function f(X, w), which minimizes the probability of misclassification using only the training data set.

Regression is a process of estimating a real-value function based on a finite data set of noisy samples. A common loss function for regression is the squared error measure

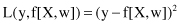
The corresponding risk functional measures the
accuracy
of the learning machine’s predictions of the system output. Maximum accuracy will be obtained by minimizing the risk functional because, in that case, the approximating function will describe the best set of given samples. Classification and regression are only two of many typical learning tasks. For the other data-mining tasks, different loss functions may be selected and they are supported with different interpretations of a risk functional.

What is a learning procedure? Or how should a learning machine use training data? The answer is given by the concept known as
inductive principle
. An inductive principle is a general prescription for obtaining an estimate f(X,w
_opt
*) in the class of approximating functions from the available finite training data. An inductive principle tells us
what
to do with the data, whereas the learning method specifies
how
to obtain an estimate. Hence a learning method or learning algorithm is a constructive implementation of an inductive principle. For a given inductive principle, there are many learning methods corresponding to a different set of functions of a learning machine. The important issue here is to choose the candidate models (approximating functions of a learning machine) of the right complexity to describe the training data.

The mathematical formulation and formalization of the learning problem explained in this section may give the unintended impression that learning algorithms do not require human intervention, but this is clearly not the case. Even though available literature is concerned with the formal description of learning methods, there is an equally important, informal part of any practical learning system. This part involves such practical and human-oriented issues as selection of the input and output variables, data encoding and representation, and incorporating a priori domain knowledge into the design of a learning system. In many cases, the user also has some influence over the generator in terms of the sampling rate or distribution. The user very often selects the most suitable set of functions for the learning machine based on his/her knowledge of the system. This part is often more critical for an overall success than the design of the learning machine itself. Therefore, all formalizations in a learning theory are useful only if we keep in mind that inductive learning is a process in which there is some overlap between activities that can be formalized and others that are not a part of formalization.

4.2 SLT

SLT is relatively new, but it is perhaps one of the best currently available formalized theories for finite-sample inductive learning. It is also known as the Vapnik-Chervonenkis (VC) theory. It rigorously defines all the relevant concepts for inductive learning and provides mathematical proofs for most inductive-learning results. In contrast, other approaches such as neural networks, Bayesian inference, and decision rules are more engineering-oriented, with an emphasis on practical implementation without needing strong theoretical proofs and formalizations.

SLT effectively describes statistical estimation with small samples. It explicitly takes into account the sample size and provides quantitative description of the trade-off between the complexity of the model and the available information. The theory includes, as a special case, classical statistical methods developed for large samples. Understanding SLT is necessary for designing sound, constructive methods of inductive learning. Many nonlinear learning procedures recently developed in neural networks, artificial intelligence, data mining, and statistics can be understood and interpreted in terms of general SLT principles. Even though SLT is quite general, it was originally developed for pattern recognition or classification problems. Therefore, the widely known, practical applications of the theory are mainly for classification tasks. There is growing empirical evidence, however, of successful application of the theory to other types of learning problems.

The goal of inductive learning is to estimate unknown dependencies in a class of approximating functions using available data. The optimal estimate corresponds to the minimum expected risk functional that includes general distribution of data. This distribution is unknown, and the only available information about distribution is the finite training sample. Therefore, the only possibility is to substitute an unknown
true risk functional
with its approximation given as
empirical risk
, which is computable based on the available data set. This approach is called ERM and it represents the basic inductive principle. Using the ERM inductive principle, one seeks to find a solution f(X, w*) that minimizes the empirical risk expressed through the training error as a substitute for the unknown true risk, which is a measure of the true error on the entire population. Depending on the chosen loss function and the chosen class of approximating functions, the ERM inductive principle can be implemented by a variety of methods defined in statistics, neural networks, automatic learning, and so on. The ERM inductive principle is typically used in a learning setting where the model is given or approximated first and then its parameters are estimated from the data. This approach works well only when the number of training samples is large relative to the prespecified model complexity, expressed through the number of free parameters.