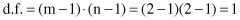Data Mining (46 page)
Authors: Mehmed Kantardzic
Correspondence analysis represents the set of categorical data for analysis within incidence matrices, also called
contingency tables
. The result of an analysis of the contingency table answers the question: Is there a relationship between analyzed attributes or not? An example of a 2 × 2 contingency table, with cumulative totals, is shown in Table
5.5
. The table is a result of a survey to examine the relative attitude of males and females about abortion. The total set of samples is 1100 and every sample consists of two categorical attributes with corresponding values. For the attribute
sex
, the possible values are male and female, and for attribute s
upport
the values are yes and no. Cumulative results for all the samples are represented in four elements of the contingency table.
TABLE 5.5.
A 2 × 2 Contingency Table for 1100 Samples Surveying Attitudes about Abortion

Are there any differences in the extent of support for abortion between the male and the female populations? This question may be translated to: What is the level of dependency (if any) between the two given attributes: sex and support? If an association exists, then there are significant differences in opinion between the male and the female populations; otherwise both populations have a similar opinion.
Having seen that log-linear modeling is concerned with association of categorical variables, we might attempt to find some quantity (measure) based on this model using data in the contingency table. But we do not do this. Instead, we define the algorithm for feature association based on a comparison of two contingency tables:
1.
The first step in the analysis is to transform a given contingency table into a similar table with
expected
values. These expected values are calculated under assumption that the variables are independent.
2.
In the second step, we compare these two matrices using the squared distance measure and the chi-square test as criteria of association for two categorical variables.
The computational process for these two steps is very simple for a 2 × 2 contingency table. The process is also applicable for increased dimensions of a contingency table (analysis of categorical variables with more than two values, such as 3 × 4 or 6 × 9).
Let us introduce the notation. Denote the contingency table as X
m
×
n
. The row totals for the table are
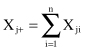
and they are valid for every row (j = 1, … , m). Similarly, we can define the column totals as
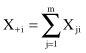
The grand total is defined as a sum of row totals:
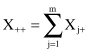
or as a sum of column totals:
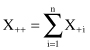
Using these totals we can calculate the contingency table of expected values under the assumption that there is no association between the row variable and the column variable. The expected values are
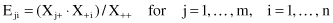
and they are computed for every position in the contingency table. The final result of this first step will be a totally new table that consists only of expected values, and the two tables will have the same dimensions.
For our example in Table
5.5
, all sums (columns, rows, and grand total) are already represented in the contingency table. Based on these values we can construct the contingency table of expected values. The expected value on the intersection of the first row and the first column will be
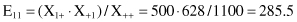
Similarly, we can compute the other expected values and the final contingency table with expected values will be as given in Table
5.6
.
TABLE 5.6.
A 2 × 2 Contingency Table of Expected Values for the Data Given in Table
5.5

The next step in the analysis of categorical-attributes dependency is the application of the chi-squared test of association. The initial hypothesis H
0
is the assumption that the two attributes are unrelated, and it is tested by Pearson’s chi-squared formula:
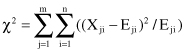
The greater the value of χ
2
, the greater the evidence against the hypothesis H
0
is. For our example, comparing Tables
5.5
and
5.6
, the test gives the following result:
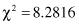
with the d.f. for an m × n dimensional table computed as