Data Mining (41 page)

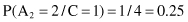
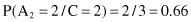
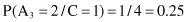
Under the assumption of conditional independence of attributes, the conditional probabilities P(X/C
_i
) will be

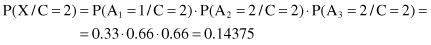
Finally, multiplying these conditional probabilities with corresponding a priori probabilities, we can obtain values proportional (≈) to P(C
_i
/X) and find their maximum:

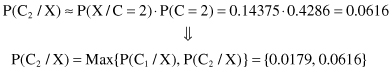
Based on the previous two values that are the final results of the Naive Bayesian classifier, we can predict that the new sample X belongs to the class C = 2. The product of probabilities for this class P(X/C = 2) · P(C = 2) is higher, and therefore P(C = 2/X) is higher because it is directly proportional to the computed probability product.

In theory, the Bayesian classifier has the minimum error rate compared with all other classifiers developed in data mining. In practice, however, this is not always the case because of inaccuracies in the assumptions of attributes and class-conditional independence.

5.4 PREDICTIVE REGRESSION

The prediction of continuous values can be modeled by a statistical technique called
regression
. The objective of regression analysis is to determine the best model that can relate the output variable to various input variables. More formally, regression analysis is the process of determining how a variable Y is related to one or more other variables x
₁
, x
₂
, … , x
_n
. Y is usually called the response output, or dependent variable, and x
_i-
s are inputs, regressors, explanatory variables, or independent variables. Common reasons for performing regression analysis include

Before explaining regression technique in details, let us explain the main differences between two concepts: interpolation and regression. In both cases training data set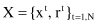
is given where x
^t
are input features and output value r
^t
∈ R.

• If there is
  no noise
  in the data set, the task is
  interpolation
  . We would like to find a function f(x) that passes through all these training points such that we have r
  ^t
  = f(x
  ^t
  ). In polynomial interpolation, given N points, we found that we can use (N − 1) degree polynomial to predict exact output r for any input x.
  
• In
  regression
  ,
  there is noise
  ε added to the output of the unknown function f: r
  ^t
  = f(x
  ^t
  ) + ε. The explanation for noise is that there are extra hidden variables z
  ^t
  that we cannot observe. We would like to approximate the output r
  ^{t
  =}
  f(x
  ^t
  , z
  ^t
  ) by our model g(x
  ^t
  ), not only for present training data but for data in future. We are minimizing empirical error: E(g/x) = 1/N Σ (r
  ^t
  − g[x
  ^t
  ])
  ²
  for t = 1 to N.
  

Generalized linear regression models are currently the most frequently applied statistical techniques. They are used to describe the relationship between the trend of one variable and the values taken by several other variables. Modeling this type of relationship is often called linear regression. Fitting models is not the only task in statistical modeling. We often want to select one of several possible models as being the most appropriate. An objective method for choosing between different models is called ANOVA, and it is described in Section 5.5.

The relationship that fits a set of data is characterized by a prediction model called a
regression equation
. The most widely used form of the regression model is the general linear model formally written as

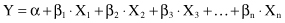
Applying this equation to each of the given samples we obtain a new set of equations