Mathematics and the Real World (25 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein
To carry out the measurements required a series of sophisticated experiments, which Michelson started in 1881; Morley joined him in 1886, and their joint efforts showed that there was no difference between the times the beam arrived back at the source. This finding raised doubts regarding the hypothesis that the ether was the medium through which light propagated.
The Dutch physicist Hendrik Lorentz proposed a mathematical formula describing the dynamics that fitted the results of the Michelson-Morley experiment. The formula corrected the assumption that until then had been considered self-evident, as it was based on what our senses perceive. The assumption was that if an object
F
is moving at a velocity
v
1
relative to object
G
, which is moving at a velocity
v
2
relative to object
H
, then
F
is moving at a velocity of
v
1
+
v
2
relative to object
H
. Lorentz proposed replacing this formula with another (whose detailed formulation is
not important for the current discussion) that showed that, at small speeds, the speed of
F
relative to
H
is very close to what our senses perceive, that is,
v
1
+
v
2
, but when
F
is moving at very high speed relative to
G
, say close to the speed of light, and
G
is moving at a speed close to the speed of light relative to
H
, then the speed of
F
relative to
H
is also close to the speed of light (and not twice that speed, as Newton's theory would infer). Lorentz also observed that if his formula is used in Maxwell's equations, the same equations are obtained in all inertial systems.
The French mathematician Henri Poincaré (1854–1912), who was then one of the most famous mathematicians in the world, stated that Lorentz's formulae gave the best explanation for the difference between Newton's laws and Maxwell's equations. He himself developed the mechanics deriving from Lorentz's transformation, and already in 1900 and later in several additional papers, he published a complete version of what later became known as the special theory of relativity, including a version of the connection between mass and energy, that is,
E
=
mc
2
. These developments of formulae presented by Lorentz were extremely close to Einstein's special theory of relativity, which we will describe below. Yet neither Lorentz, though a famous physicist who actually was awarded the Nobel Prize in Physics in 1902, nor Poincaré, nor others who tried with the help of those formulae to reconcile Newton's and Maxwell's theories drew the right conclusions from the formulae. It was Albert Einstein who did so.
Einstein (the extent of whose knowledge of these developments is unknown, as we stated above) adopted Lorentz's formulae and distilled from them a physical property that completely contradicts intuition based on our daily experiences. The property is that the speed of light is constant in every inertial system of coordinates. That is to say that if light travels at a speed of
c
relative to an object
G
, and
G
is traveling much faster than an object
H
, even at half the speed of light, the light will still travel at speed
c
relative to object
H
. This leads to the conclusion that it is not possible to get an object to move faster than the speed of light. In a certain sense, Einstein claimed that the geometry of the world, including formulae for combining speeds, is described better by Lorentz's formulae than by Newton's. As stated above, at relatively low speeds Lorentz's formulae are very close to
Newton's, which is why our intuition, which is based on our daily experiences of only relatively low speeds, led us to accept Newton's formulae as describing the world.
The mathematics that describes the new relations between position and speed brought Einstein to the realization of the possibility of something never previously envisaged, and in particular something that was opposed to our intuition (in the wake of Maxwell's basic contribution, the realization that mathematics can lead to revelations of totally new phenomena had become accepted). The equation leads to the conclusion that mass is converted to energy. This was a mathematical statement that could have remained in the realm of a technical mathematical conclusion without any physical importance. Einstein, however, interpreted the equation as a physical truth and drew the conclusion that the substitution between mass and energy was possible (although at that point in time he did not see a way to control and exploit this possibility). He even derived the famous formula
E
=
mc
2
(after several more-complex versions) from the equation for the mass-energy equivalence. Einstein published these discoveries in two papers that appeared in 1905. Three years later, in 1908, Hermann Minkowski (1864–1909), who was one of Einstein's tutors when the latter was studying at the Institute of Technology in Zurich, Switzerland, presented a new geometry in which the coordinate of time did not have special status but was to be treated like the other, spatial, coordinates. To formulate the rules of this new geometry, Minkowski developed what is called tensorial calculus, which extended Newton's system of derivatives to more complex relations. Thus the special theory of relativity became established from both the physical and the basic mathematical aspects.
An interesting question is why Einstein received all the credit for the special theory of relativity when, as noted above, its essence, including the formula
E
=
mc
2
, had been published by Poincaré before Einstein. If we ignore the conspiracy speculations that are raised from time to time, the answer has two parts. The first difference between Einstein's theory and Poincaré's is a conceptual one. Poincaré developed mathematics and did not notice, or at least did not declare and emphasize, that mathematics presents physics with new principles. Einstein focused on the physical
principles from which the new mechanics are derived, of course with the help of mathematics. Therefore, to attribute the new physics to Einstein is completely justified. (Einstein worked on his theory while in the Bern patent office, before he learned of all of Poincaré's findings.) The second part of the answer is that Poincaré's papers are densely written and hard to read, whereas Einstein immediately concentrated on the essence and the new, and he presented his theory in an almost intuitive way. For example, Poincaré gave the mass/energy ratio as
m
=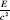 , an expression that is harder to grasp than the more familiar version. Simplicity has a clear advantage.
, an expression that is harder to grasp than the more familiar version. Simplicity has a clear advantage.
The special theory of relativity unified Newton's mechanics with the electromagnetic mechanics of Maxwell; in other words, it gave a joint mathematical system to both physical phenomena. The mathematical analysis of speeds significantly below the speed of light in effect coincides with Newton's theory. The effects related to the theory of relativity emerge only at speeds close to the speed of light. In classic engineering situations, the use of Newton's formulae is accurate enough, and for many years the part of the theory that related to relativity was in the domain only of scientists. In the current era, when for example communication at the speed of light is relevant to everyone, the equations that describe relativity are in widespread engineering use.
One Newtonian law of nature, gravity, remains outside the mathematical framework of special relativity. Moreover, Newton's second law and the law of gravity both relate to mass, the same mass. If these are different laws there is no reason for the same physical quantity to serve both. Einstein suggested that the two laws were two aspects of the same effect. The example he gave to make the point was a free fall in an elevator, that is, an elevator whose cable has broken and is falling freely, inside which, although a passenger is accelerating due to the force of gravity, he is not aware of any force being exerted. That is, the exertion of the force is also relative. Unlike the case of special relativity, where the mathematics had already been developed and Einstein's main contribution was to present the physical interpretation, in the analysis of gravity Einstein first posed the physical hypothesis. Without mathematics, however, the hypothesis had no
scientific value. Einstein devoted several years of research to the attempt to find a mathematical theory that would unify gravity and the other forces, published a number of articles with partial results, and finally, in 1916, published the definitive paper presenting the general theory of relativity. Once again the solution required a new presentation of the geometry of the world. The mathematical framework Einstein used was that proposed by Riemann some sixty years earlier (see the previous section), and the mathematical tool that describes the mechanics in this geometric world was the tensor calculus that Minkowski developed to show the geometry of the world of special relativity.
Einstein adopted Galileo and Newton's idea of inertia, but he adopted the version that stated that a body that has no force exerted on it will continue to move along a geodesic, that is, the shortest line between two points in a space. Then Einstein claimed that in the geometry of the physical space, the shortest line between two points in this space is not a Newtonian straight line but a line that is seen in Newtonian space as a curved line. Moreover, the factor causing the curvature of the line is the existence of mass. According to this description, the gravitational attraction is only the result of a geometrical feature. For example, we think that the Sun attracts the Earth, and that is why the Earth does not continue in a straight line but revolves around the Sun; in effect what happens is that the Sun distorts the space in such a way that the elliptical orbit of the Earth is actually a “straight line” in the sense that it is the shortest route in the geometry of the space. Is this merely playing with words, or are we dealing with a physical feature that our senses did not perceive previously? The test will be whether the theory explains things that cannot be explained any other way, and it will be even more convincing if it predicts new effects.
One aspect that Einstein explained using the new geometry was the very small changes discovered in the path of the planet Mercury. Astronomers had proposed other explanations for those variations, such as the effect of another as yet undiscovered planet. Einstein also proposed a new prediction. If it is geometry that is the determining factor, then a physical body on which ordinary gravity ought not to act would follow the curved line that Einstein forecasts and would not follow a Newtonian straight line.
Light itself is such a physical object. If physical space curves around the Sun, then the light of a star that reaches us and that passes around the Sun will reach us on a curved route and will seem to us to be in a different location. We do not generally see the light of stars coming from the direction of the Sun. The best time to identify and measure the direction from which the light is arriving is during a full eclipse of the Sun. A number of scientific expeditions tried to check Einstein's prediction over several years but failed either because of bad atmospheric conditions when the sky was hidden by clouds precisely at the time of the eclipse or because of political events, such as when an eclipse of the Sun occurred in the middle of a war between Germany and Russia and the expedition's astronomical equipment was confiscated by the Russian authorities who were concerned about espionage.
The confirmation came on May 29, 1919, when there was one of the longest total eclipses of the Sun, lasting almost seven minutes. The eclipse started in Brazil and moved to South Africa. Two expeditions were organized by the British Royal Society; one went to Brazil, and the other to a small island off the coast of South Africa. Both of them managed to measure and corroborate Einstein's general theory of relativity. Later, doubts were expressed whether the equipment they had used was accurate enough to enable the conclusions they had reached to be drawn. In any event, since then the general theory of relativity has been confirmed many times. Einstein's equations correctly describe the geometry of the world. As was the case with the special theory of relativity, the general theory was also for many years relevant only to scientists. Today, with the wide use of outer space, for instance for GPSs (global positioning systems), effects that are part of general relativity are also relevant to engineering.
But even Einstein, the master of intuitive interpretations of mathematics, was not immune from the trickery of intuition. The common perception was that the gravitational force will, eventually, cause the universe the collapse. Einstein's intuition told him that the universe is static, and he corrected the equation by adding a constant, the
cosmological constant, that stabilizes the equations. Later, Edwin Hubble discovered that the universe is indeed expanding, and with a constant rate. Einstein removed the cosmological constant from the equations, referring to the addition of the constant as the biggest mistake in his scientific life. This can be interpreted as saying that, had he believed in the original equations, he could have predicted the expansion of the universe before it was discovered by analysis of experimental data. Recently it was discovered that the expansion itself is accelerated. This can be explained by putting back the cosmological constant into the equations, this time to account for the acceleration of the expansion. Thus, it could turn out that the removal of the constant from the equation was another mistake by Einstein.