The Amazing Story of Quantum Mechanics (4 page)
Read The Amazing Story of Quantum Mechanics Online
Authors: James Kakalios
“The Skylark of Space” leaves vague the exact nature of the “intra-atomic energy” released by the copper when catalyzed by Element X and an electrical current. A rival scientist of Seaton’s puts it as follows: “Chemists have known for years that all matter contains enormous stores of intra-atomic energy, but have always considered it ‘bound’—that is, incapable of liberation. Seaton has liberated it.” As chemists certainly knew, even in 1928, how to release the energy stored in chemical bonds between atoms in molecules such as nitroglycerin or TNT, the vast amounts of intra-atomic energy liberated by Element X may refer to the conversion of mass into energy through Einstein’s relationship E = mc
2
. This seems likely; when a spaceship propelled by Element X is accidently set to full thrust, the resulting acceleration becomes so great that no one on board can move to the control board to decrease their speed and the ship stops its motion only when the copper supplies are exhausted. While illustrating Einstein’s principle of the interrelation between energy and mass, this scene contradicts the Special Theory of Relativity when it reveals that this uncontrolled acceleration has resulted in the ship traveling many times the speed of light. When Seaton wonders how this can be reconciled with Einstein’s famous work, his companion replies, “That is a theory, this measurement of distance is a fact, as you know from our tests.” Like any good scientist, Seaton agrees that observation is the final arbiter of correctness and concludes of Einstein, “That’s right. Another good theory gone to pot.”
2
. This seems likely; when a spaceship propelled by Element X is accidently set to full thrust, the resulting acceleration becomes so great that no one on board can move to the control board to decrease their speed and the ship stops its motion only when the copper supplies are exhausted. While illustrating Einstein’s principle of the interrelation between energy and mass, this scene contradicts the Special Theory of Relativity when it reveals that this uncontrolled acceleration has resulted in the ship traveling many times the speed of light. When Seaton wonders how this can be reconciled with Einstein’s famous work, his companion replies, “That is a theory, this measurement of distance is a fact, as you know from our tests.” Like any good scientist, Seaton agrees that observation is the final arbiter of correctness and concludes of Einstein, “That’s right. Another good theory gone to pot.”
The scientists in “The Skylark of Space” should not be so quick to abandon Einstein, for their X-plosive bullets of intra-atomic energy provide confirmation of another of his theories. This application of Element X, as well as the ray guns wielded by Buck Rogers, Flash Gordon, and other heroes of the science fiction pulps and comic strips, is not too far from the mark, as reflected in the first quantum principle, at the top of this chapter. As proposed by Albert Einstein the same year he developed his Special Theory of Relativity, all light consists of “bullets,” that is, discrete packets of energy, termed “photons.”
Now that we have the answers to quantum mechanics—what were the questions that called for these new physical principles? The ultraviolet catastrophe alluded to earlier concerned the brightness of the light emitted by an object as a function of temperature. Certain objects, such as graphite and coal dust, are black, as they absorb nearly all light that shines on them. In equilibrium, the light energy absorbed is balanced by light given off. The spectrum of light of such blackbodies, that is, how much light is emitted at a given frequency, depends only on how hot it is and is the same for metals, insulators, gases, liquids, or people if they are at the same temperature.
The theory of electromagnetic waves, developed by James Clerk Maxwell in the second half of the nineteenth century, was able to account for the energy emitted by a glowing object at low frequencies, such as infrared light, but at higher frequencies (above visible light) this theory predicted results that were nonsensical. Calculations indicated that the light from any heated object would become infinitely intense at high frequencies, above the ultraviolet portion of the spectrum. Thus, anyone looking at the glowing embers in a fireplace, or the interior of an oven, should be instantly incinerated with a lethal dose of X-rays. If this were true, most people would notice. This so-called ultraviolet catastrophe (which, as indicated, was a catastrophe more for theoreticians making the predictions than for anyone else) disappeared following Planck’s suggestion that when the atoms in a glowing object emit light, the atoms lose energy as if they were moving down the steps of a ladder, and that those atoms must always move from rung to rung of the ladder and cannot make any other transitions between rungs. Why this would resolve the ultraviolet catastrophe, we’ll explain in Section 4. For now let’s focus on this “ladder” of possible energy values.
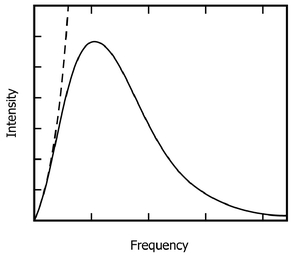
Figure 2:
A plot of the light intensity given off from a “blackbody” object as a function of the frequency of light. The measured curve (solid line) shows that the total amount of light emitted is finite, while the pre-quantum mechanics calculated curve (dashed line) continues to rise as the frequency of light increases. That is, before quantum mechanics, physics predicted that even objects at room temperature would give off an infinite amount of light energy in the ultraviolet portion of the spectrum—a clearly ridiculous result.
A plot of the light intensity given off from a “blackbody” object as a function of the frequency of light. The measured curve (solid line) shows that the total amount of light emitted is finite, while the pre-quantum mechanics calculated curve (dashed line) continues to rise as the frequency of light increases. That is, before quantum mechanics, physics predicted that even objects at room temperature would give off an infinite amount of light energy in the ultraviolet portion of the spectrum—a clearly ridiculous result.
Planck firmly believed that light was a continuous electromagnetic wave, like ripples on the surface of a lake,
6
as theoretical considerations and extensive experimental evidence indicated. His proposal of discreteness in atomic energy loss was fairly modest (or as modest as a revolution in scientific thought can be). It turns out that while Planck justly receives credit for letting the quantum genie out of the bottle, there were other experimental conundrums waiting in the wings regarding how atoms interacted with light that would require far bolder steps than Planck was willing to take. At the same time that scientists were measuring the light given off by hot objects, giving rise to the ultraviolet catastrophe, Philipp Lenard was studying the electrons emitted by metals exposed to ultraviolet light. This led to a different catastrophe, both personal and scientific.
6
as theoretical considerations and extensive experimental evidence indicated. His proposal of discreteness in atomic energy loss was fairly modest (or as modest as a revolution in scientific thought can be). It turns out that while Planck justly receives credit for letting the quantum genie out of the bottle, there were other experimental conundrums waiting in the wings regarding how atoms interacted with light that would require far bolder steps than Planck was willing to take. At the same time that scientists were measuring the light given off by hot objects, giving rise to the ultraviolet catastrophe, Philipp Lenard was studying the electrons emitted by metals exposed to ultraviolet light. This led to a different catastrophe, both personal and scientific.
In the late 1800s physicists had discovered that certain materials, such as radium and thorium, gave off energy in the form of what would eventually be termed “radiation.” Scientific researchers entered a “library phase,” cataloging all of the different types of radiation that different substances emitted. Using the Greek alphabet as labels (α, β, γ, etc., instead of a, b, c, and so on), they started with “alpha rays,” which turned out to be helium nuclei (two protons and two neutrons) ejected from atoms found near the end of the periodic table of the elements,
7
then moved on to “beta rays,” (high-speed electrons), followed by “gamma rays” (very high-energy electromagnetic radiation).
8
When William Roentgen discovered a form of radiation that would fog a photographic plate, passing through paper or flesh but not metal or bones, he termed this unknown ra diation “X-rays.” Roentgen’s discovery came before the Greek nomenclature tradition used for naming rays; he used the letter
X,
as it is the letter traditionally employed in math problems for the unknown quantity. (Roentgen’s “X-rays” were the forerunner of many science fiction
X
-based characters, such as the X-Men, Professor X, Planet X, Dimension X, Element X, and X the Unknown). It was later shown that X-rays are simply electromagnetic waves—that is, light—with more energy than visible and ultraviolet light but less energy than gamma rays.
7
then moved on to “beta rays,” (high-speed electrons), followed by “gamma rays” (very high-energy electromagnetic radiation).
8
When William Roentgen discovered a form of radiation that would fog a photographic plate, passing through paper or flesh but not metal or bones, he termed this unknown ra diation “X-rays.” Roentgen’s discovery came before the Greek nomenclature tradition used for naming rays; he used the letter
X,
as it is the letter traditionally employed in math problems for the unknown quantity. (Roentgen’s “X-rays” were the forerunner of many science fiction
X
-based characters, such as the X-Men, Professor X, Planet X, Dimension X, Element X, and X the Unknown). It was later shown that X-rays are simply electromagnetic waves—that is, light—with more energy than visible and ultraviolet light but less energy than gamma rays.
These varieties of radiation provided scientists at the end of the nineteenth century with new tools to study matter. By exposing different materials to these forms of radiation and observing their effect, they could probe the inner working of atoms. They were able, for the first time, to metaphorically take off the back plate and examine the mechanisms inside the atomic watches. Admittedly this tool was more like a hammer than a jeweler’s screwdriver, but you use what you have.
Lenard was working at the University of Heidelberg and investigating the influence of light exposure on various metals. He discovered through a series of careful experiments that certain metals, when illuminated with ultraviolet light, give off beta rays, that is, electrons. It would turn out that the electrons he was observing originated from the sea of electrons that explain why all metals are good conductors of heat and electricity. This, in hindsight, is not that surprising. Light carries energy, and when an object absorbs energy it warms up. Some of the excess energy in the metal can be transferred to the electrons, and if they are sufficiently energetic they can fly free, not unlike the energetic water molecules leaving the liquid surface of a hot cup of coffee and forming a cloud of steam above the mug. Philipp Lenard set about systematically investigating how the number of electrons emitted from a given metal and their speed depended on the frequency and intensity of the ultraviolet light he used. Here the troubles began.
Imagine a metal as a sandy beach at the ocean’s shore, and the electrons in the metal as small pebbles randomly scattered along the beach (see Figure 3). The ocean waves crashing onto the beach can be considered the ultraviolet electromagnetic waves shining on the metal in Lenard’s experiment. This allegorical beach has a gentle slope away from the water’s edge, so that one must do work against gravity to push the pebbles away from the shoreline. When the pebbles have advanced up the beach all the way to the boardwalk, we’ll consider them free, and as our stand-ins for electrons in a metal, they will represent those electrons that are ejected from the solid by the ultraviolet light in Lenard’s experiment. In this analogy it is reasonable that the energy responsible for picking up the pebbles and moving them up the beach comes from the water waves. The bigger the wave, the more energy the pebbles will have. The more frequently the waves arrive, the greater the number of pebbles will be advanced. If the waves have small amplitudes, one might have to patiently wait for several wave fronts to transfer sufficient energy to the pebbles before they can move up the beachfront. Perfectly reasonable—except this was not what Lenard observed.
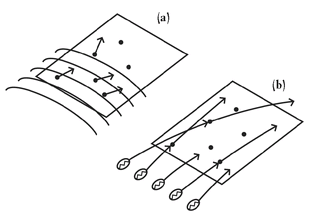
Figure 3:
Cartoon sketch of pebbles on a beach, pushed up toward the top of the beach by either ocean waves (a) or by photon bullets (b).
Cartoon sketch of pebbles on a beach, pushed up toward the top of the beach by either ocean waves (a) or by photon bullets (b).
He found that the energy of the electron leaving the metal did not depend on the intensity of the light. Raising the light intensity did not affect the electron’s speed, though it did increase the number of electrons emitted per second. But the number of electrons ejected per second was supposed to depend on the frequency of the waves, that is, how many wave crests arrived per second, and not their amplitude. Moreover, there was a threshold for electron emission—if the frequency of the light were below a certain value (which varied for different metals), then no electrons came off, regardless of how bright the light. In the water analogy, this would suggest that if the number of wave peaks per second were below a given value, then even a tsunami would not push the pebbles up the beach. What did govern whether or not the electrons were emitted was the frequency of the light. For the beach analogy, this would be as if once the number of wave peaks per second rose above a certain threshold, then even a very low-amplitude, gentle wave would promote pebbles up to the boardwalk, just as long as the time between crests was short enough. Finally, if the frequency of the light was above this threshold, then electrons came off instantly, with no time delay, no matter how low the light’s intensity. These experimental results were a challenge to understand within the context of light being a continuous electromagnetic wave, but we already know the answer to this question, stated at the start of this chapter. Light is not a continuous wave but is composed of individual energy bullets, termed “photons.”
How does light actually consisting of discrete packets of energy explain Lenard’s experimental results? What we took to be a continuous, uniform series of waves washing up onshore, gently pushing the pebbles up the beach, is actually comprised of bullets fired at the pebbles by a machine gun sweeping back and forth across the beach. With light being a collection of photons, the brightness of the light is determined by the number of photons passing through a given area per second. For our machine gun, this is equivalent to the rate at which bullets are fired; that is, more bullets per second leads to more intense illumination. One bullet a second is a weak light source, while a million shots per second is much brighter. The energy of the photons would be reflected in our analogy in the speed of the bullets (let’s suppose for the sake of argument that we have a magical machine gun that provides independent control over the speed of the bullets it fires).
Other books
Los tres mosqueteros by Alexandre Dumas
Silencio sepulcral by Arnaldur Indridason
Out of The Woods by Patricia Bowmer
Half-Sick of Shadows by David Logan
The Man in 3B by Weber, Carl
Shared by Eight Strangers by Marsh, Lia
Uncaged Love Volume 5 by J. J. Knight
King of Prey: (A Bird Shifter Novel) by Roth, Mandy M.
09 The Clue at Black Creek Farm by Carolyn Keene
Novel - The Supernaturalist by Eoin Colfer