What Technology Wants (25 page)
Read What Technology Wants Online
Authors: Kevin Kelly
In this microcosmic realm, unlike the macroworld we live in, energy is not very important. That is why we don't see a Moore's Law type of progress at work when scaling up: energy requirements scale up just as fast, and energy is a major limiting constraint, unlike information, which can be duplicated freely. This is also why we don't see exponential progress in the performance of solar panels (only linear progress) or batteriesâbecause they generate or store lots of energy. So our entire new economy is built around technologies that need little energy and scale down wellâphotons, electrons, bits, pixels, frequencies, and genes. As these inventions miniaturize, they reach closer to bare atoms, raw bits, and the essence of the immaterial. And so the fixed and inevitable path of their progress derives from this elemental essence.
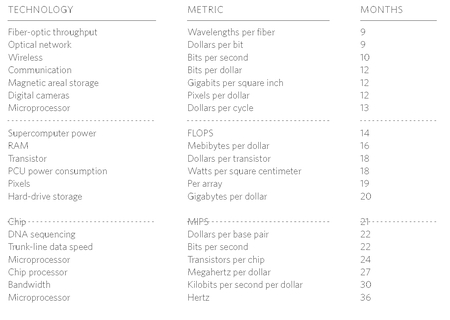
Doubling Times.
Performance ratios of various technologies measured as the number of months required to double their performance.
Performance ratios of various technologies measured as the number of months required to double their performance.
The second thing to notice about this set of examples is the narrow range of slopes, or doubling time (in months). The particular power being optimized in these technologies is doubling in between 8 and 30 months. (Moore's Law calls for doubling every 18 months.) Every one of these parameters is getting twice as better every year or two. What's up with that? Engineer Mark Kryder's explanation is that “twice as better every two years” is an artifact of corporate structure, where most of these inventions happen. It just takes one to two years of calendar time to conceive, design, prototype, test, manufacture, and market a new improvement, and while a five- or 10-fold increase is very difficult to achieve, almost any engineer can deliver a factor of two. Voila! Twice as better every two years. If true, this suggests that while the steady trajectory of progress stems directly from the technium, the actual angle of incline is not a supernatural number (doubling every 18 months) but is simply dependent on human work cycles.
At the moment there is no end in sight for any of these curves, but at some point in the future, each curve will plateau. Moore's Law will not continue forever. That's just life. Any specific exponential growth will inevitably smooth out into a typical
S
-shaped curve. This is the archetypal pattern of growth: After a slow ramp-up, gains take off straight up like a rocket, and then after a long run level out slowly. Back in 1830 only 37 kilometers of railroad track had been laid in the United States. That count doubled in the next ten years, and then doubled in the decade after that, and kept doubling every decade for 60 years. In 1890 any reasonable railroad buff would have predicted that the United States would have hundreds of millions of kilometers of railroad by a hundred years later. There would be railroad to everyone's house. Instead, there were fewer than 400,000 kilometers. However, Americans did not cease to be mobile. We merely shifted our mobility and transportation to other species of invention. We built automobile highways and airports. The miles we travel keep expanding, but the exponential growth of that particular technology peaked and plateaued.
S
-shaped curve. This is the archetypal pattern of growth: After a slow ramp-up, gains take off straight up like a rocket, and then after a long run level out slowly. Back in 1830 only 37 kilometers of railroad track had been laid in the United States. That count doubled in the next ten years, and then doubled in the decade after that, and kept doubling every decade for 60 years. In 1890 any reasonable railroad buff would have predicted that the United States would have hundreds of millions of kilometers of railroad by a hundred years later. There would be railroad to everyone's house. Instead, there were fewer than 400,000 kilometers. However, Americans did not cease to be mobile. We merely shifted our mobility and transportation to other species of invention. We built automobile highways and airports. The miles we travel keep expanding, but the exponential growth of that particular technology peaked and plateaued.
Much of the churn in the technium is due to our tendency to shift what we care about. Mastering one technology engenders new technological desires. A recent example: The first digital cameras had very rough picture resolution. Then scientists began cramming more and more pixels onto one sensor to increase photo quality. Before they knew it, the number of pixels possible per array was on an exponential curve, heading into megapixel territory and beyond. The rising megapixel count became the chief selling point for new cameras. But after a decade of acceleration, consumers shrugged off the increasing number of pixels because the current resolution was sufficient. Their concern instead shifted to the speed of the pixel sensors or the response in low lightâthings no one had cared about before. So a new metric is born, and a new curve started, and the exponential curve of ever more pixels per array will gradually abate.
Moore's Law is headed to a similar fate. When, no one knows. Decades ago Gordon Moore himself predicted his law would end when it reached 250-nanometer manufacturing, which it passed in 1997. Today the industry is aiming for 20 nanometers. Whether Moore's Lawâas the count of transistor densityâhas one, two, or three decades left to zoom and drive our economy, we can be sure it will peter out as other past trends have by being sublimated into another rising trend. As the old Moore's Law abates, we'll find alternative solutions to making a million times more transistors. In fact, we may already have enough transistors per chip to do what we want, if only we knew how.
Moore began by measuring the number of “components” per square inch, then switched to transistors; now we measure transistors per dollar. Just as happened in pixel counts, once one exponential trend in computer chips (say, the density of transistors) decelerates, we begin caring about a new parameter (say, speed of operations or number of connections), and so we begin measuring a new metric and plotting a new graph. Suddenly, another “law” is revealed. As the character of this new technique is studied, exploited, and optimized, its natural pace is revealed, and when this trajectory is extrapolated, it becomes the creators' goal. In the case of computing, this newly realized attribute of microprocessors will become, over time, the new Moore's Law.
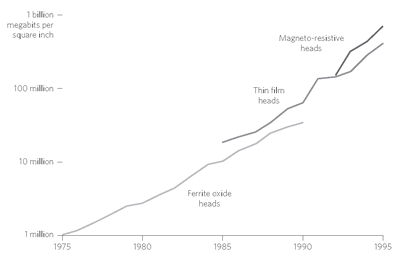
The Continuum of Kryder's Law.
Improvements in the recording density of magnetic technologies continue uninterrupted across different technological platforms.
Improvements in the recording density of magnetic technologies continue uninterrupted across different technological platforms.
Like the Air Force's 1953 graph of top speed, the curve is one way the technium speaks to us. Carver Mead, who barnstormed the country waving plots of Moore's Law, believes we need to “listen to the technology.” The curves speak in concert. As one curve inevitably flattens out, its momentum is taken up by another
S
curve. If we inspect any enduring curve closely, we can see how definitions and metrics shift over time to accommodate new substitute technologies.
S
curve. If we inspect any enduring curve closely, we can see how definitions and metrics shift over time to accommodate new substitute technologies.
For instance, close scrutiny of Kryder's Law in hard-disk densities shows that it is composed of a sequence of overlapping smaller trend lines. The first hard-disk technology, ferrite oxide, ran from 1975 to 1990. The second technology, thin film, had a slightly better performance and slightly faster acceleration and overlapped ferrite oxide, running from 1985 to 1995. The third technological innovation, magneto resistance, began in 1993 and improved at a still faster rate. Their slightly uneven slopes combine to yield an unwavering trajectory.
The graph below dissects what is happening for a generic technology. A stack of
S
curves, each one containing its own limited run of exponential growth, overlap to produce a long-run emergent exponential growth line. The megatrend bridges more than one technology, giving it a transcendent power. As one exponential boom is subsumed into the next, an established technology relays its momentum to the next paradigm and carries forward an unrelenting growth. The exact unit of what is being measured can also morph from one subcurve to the next. We may start out counting pixel size, then shift to pixel density, then to pixel speed. The final performance trait may not be evident in the initial technologies and reveal itself only over the long term, perhaps as a macrotrend that continues indefinitely. In the case of computers, as the performance metric of chips is constantly recalibrated from one technological stage to the next, Moore's Lawâredefinedâwill never end.
S
curves, each one containing its own limited run of exponential growth, overlap to produce a long-run emergent exponential growth line. The megatrend bridges more than one technology, giving it a transcendent power. As one exponential boom is subsumed into the next, an established technology relays its momentum to the next paradigm and carries forward an unrelenting growth. The exact unit of what is being measured can also morph from one subcurve to the next. We may start out counting pixel size, then shift to pixel density, then to pixel speed. The final performance trait may not be evident in the initial technologies and reveal itself only over the long term, perhaps as a macrotrend that continues indefinitely. In the case of computers, as the performance metric of chips is constantly recalibrated from one technological stage to the next, Moore's Lawâredefinedâwill never end.
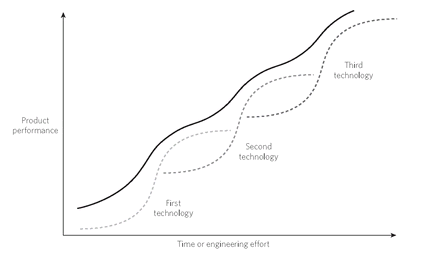
Compound
S
Curves.
On this idealized chart, technological performance is measured on the vertical axis and time or engineering effort captured on the horizontal. A series of sub-
S
curves create an emergent larger-scale invariant slope.
S
Curves.
On this idealized chart, technological performance is measured on the vertical axis and time or engineering effort captured on the horizontal. A series of sub-
S
curves create an emergent larger-scale invariant slope.
The slow demise of the more-transistors-per-chip trend is inevitable. But on average, digital technologies will roughly double in performance every two years for the foreseeable future. That means our most culturally important devices and systems will get faster, cheaper, better by 50 percent every year. Imagine if you got half again smarter every year or could remember 50 percent more this year than last. Embedded deep in the technium (as we now know it) is the remarkable capacity of half-again annual improvement. The optimism of our age rests on the reliable advance of Moore's promise: that stuff will get significantly, seriously, desirably better and cheaper tomorrow. If the things we make will get better the next time, that means that the golden age is ahead of us, and not in the past. But if Moore's Law ceased, would our optimism end, too?
Even if it we wanted to, what on Earth could derail the long version of Moore's Law? Suppose we were part of a vast conspiracy to halt Moore's Law. Maybe we believed it elevates undue optimism and encourages misguided expectations of a super artificial intelligence that will bring us immortality. What could we do? How would you stop it? Those who believe its power rests primarily in its self-reinforced expectations would say: Simply announce that Moore's Law will end. If enough smart believers declare Moore's Law over, then it will be over. The loop of self-fulfilling prophecy would be broken. But all it takes is one maverick to push ahead and make further progress, and the spell would be broken. The race would resume until the physics of scaling down gave out.
More clever folk might reason that since the economic regime as a whole determines the doubling time of Moore's Law, you could keep decreasing the quality of the economy until it stopped. Perhaps through armed revolution you could install an authoritative command-style policy (like an old state communism) whose lackadaisical economic growth would kill the infrastructure for exponential increases in computing power. I find that possibility intriguing, but I have my doubts. If in a counterfactual history, communism had won the cold war and microelectronics had been invented in a global Soviet-style society, my guess is that even that alternative policy apparatus could not stifle Moore's Law. Progress might roll out slower at a lower slope, maybe with a doubling time of five years, but I don't doubt that Stalinist scientists would tap into the law of the microcosm and soon marvel at the same technical wonder we do: chips improving exponentially as constant linear effort is applied.
I suspect Moore's Law is something we don't have much sway over, other than its doubling period. Moore's Law is the Moirae of our age. In Greek mythology the Moirae were the three Fates, usually depicted as dour spinsters. One Moira spun the thread of a newborn's life. The other Moira counted out the thread's length. And the third Moira cut the thread at death. A person's beginning and end were predetermined. But what happened in between was not inevitable. Humans and gods could work within the confines of one's ultimate destiny.
The unbending trajectories uncovered by Moore, Kryder, Roberts, Carlson, and Kurzweil spin through the technium, forming a long thread. The direction of the thread is inevitable, destined by the nature of matter and discovery. But its meander is open, left for us to finish.
Other books
Magic Parcel by Frank English
Birth of a Bridge by Maylis de Kerangal
De la dictadura a la democracia by Gene Sharp
Disappearing Home by Deborah Morgan
The Venice Conspiracy by Jon Trace
Nurse Kelsey Abroad by Marjorie Norrell
Audition by Ryu Murakami
Rebound (Pro-U Book 3) by Ali Parker
At Close Quarters by Eugenio Fuentes