Data Mining (136 page)
Authors: Mehmed Kantardzic
we will obtain
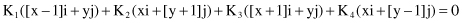
Both the i and j components of the previous vector have to be equal to 0, and therefore:
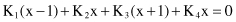
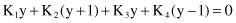
or
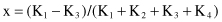
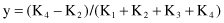
These are the basic relations for representing a 4-D point P*(K
1
,K
2
,K
3
,K
4
) in a 2-D space P(x, y) using the radial-visualization technique. Similar procedures may be performed to get transformations for other n-dimensional spaces.
We can analyze the behavior of n-dimensional points after transformation and representation with two dimensions. For example, if all n coordinates have the same value, the data point will lie exactly in the center of the circle. In our 4-D space, if the initial point is P
1
*(0.6, 0.6, 0.6, 0.6), then using relations for x and y its presentation will be P
1
(0, 0). If the n-dimensional point is a unit vector for one dimension, then the projected point will lie exactly at the fixed point on the edge of the circle (where the spring for that dimension is fixed). Point P
2
*(0, 0, 1, 0) will be represented as P
2
(−1, 0). Radial visualization represents a nonlinear transformation of the data, which preserves certain symmetries. This technique emphasizes the relations between dimensional values, not between separate, absolute values. Some additional features of radial visualization include:
1.
Points with approximately equal coordinate values will lie close to the center of the representational circle. For example, P
3
*(0.5, 0.6, 0.4, 0.5) will have 2-D coordinates P
3
(0.05, −0.05).
2.
Points that have one or two coordinate values greater than the others lie closer to the origins of those dimensions. For example, P
4
*(0.1, 0.8, 0.6, −0.1) will have a 2-D representation P
4
(−0.36, −0.64). The point is in a third quadrant closer to D2 and D3, points where the spring is fixed for the second and third dimensions.
3.
An n-dimensional line will map to the line or in a special case to the point. For example, points P
5
*(0.3, 0.3, 0.3, 0.3), P
6
*(0.6, 0.6, 0.6, 0.6), and P
7
*(0.9, 0.9, 0.9, 0.9) are on a line in a 4-D space, and all three of them will be transformed into the same 2-D point P
567
(0, 0).
4.
A sphere will map to an ellipse.
5.
An n-dimensional plane maps to a bounded polygon.
The
Gradviz method
is a simple extension of a radial visualization that places the dimensional anchors on a rectangular grid instead of the perimeter of a circle. The spring forces work the same way. Dimensional labeling for
Gradviz
is difficult, but the number of dimensions that can be displayed increases significantly in comparison to the Radviz technique. For example, in a typical Radviz display 50 seems to be a reasonable limit to the points around a circle. However, in a grid layout supported by the Gradviz technique you can easily fit 50 × 50 grid points or dimensions into the same area.
15.5 VISUALIZATION USING SELF-ORGANIZING MAPS (SOMs)
SOM is often seen as a promising technique for exploratory analyses through visualization of high-dimensional data. It visualizes a data structure of a high-dimensional data space usually as a 2-D or 3-D geometrical picture. SOMs are, in effect, a nonlinear form of PCA, and share similar goals to multidimensional scaling. PCA is much faster to compute, but it has the disadvantage, compared with SOMs, of not retaining the topology of the higher dimensional space.
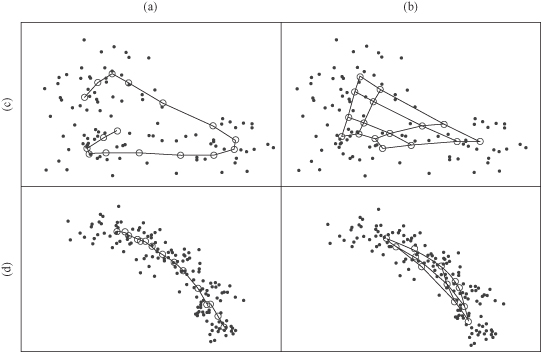
The topology of the data set in its n-dimensional space is captured by the SOM and reflected in the ordering of its output nodes. This is an important feature of the SOM that allows the data to be projected onto a lower dimension space while roughly preserving the order of the data in its original space. Resultant SOMs are then visualized using graphical representations. SOM algorithm may use different data-visualization techniques including a cell or U-matrix visualization (a distance matrix visualization), projections (mesh visualization), visualization of component planes (in a multiple-linked view), and 2-D and 3-D surface plot of distance matrices. These representations use visual variables (size, value, texture, color, shape, orientation) added to the position property of the map elements. This allows exploration of relationships between samples. A coordinate system enables to determine distance and direction, from which other relationships (size, shape, density, arrangement, etc.) may be derived. Multiple levels of detail allow exploration at various scales, creating the potential for hierarchical grouping of items, regionalization, and other types of generalizations. Graphical representations in SOMs are used to represent uncovered structure and patterns that may be hidden in the data set and to support understanding and knowledge construction. An illustrative example is given in Figure
15.9
where linear or nonlinear relationships are detected by the SOM.
Figure 15.9.
Output maps generated by the SOM detect relationships in data. (a) 1-D image map; (b) 2-D image map; (c) nonlinear relationship; (d) linear relationship.
For years there has been visualization of primary numeric data using pie charts, colored graphs, graphs over time, multidimensional analysis, Pareto charts, and so forth. The counterpart to numeric data is unstructured, textual data. Textual data are found in many places, but nowhere more prominently than on the Web. Unstructured electronic data include emails, email attachments, PDF files, spread sheets, PowerPoint files, text files, and document files. In this new environment, the end user faces massive amounts, often millions, of unstructured documents. The end user cannot read them all, and especially, there is no way he/she could manually organize or summarize them. Unstructured data run the less formal part of the organization, while structured data run the formal part of the organization. It is a good assumption, confirmed in many real-world applications, that as many business decisions are made in the unstructured environment as in the structured environment.
The SOM is one efficient solution for the problems of unstructured visualization of documents and unstructured data. With a properly constructed SOM, you can analyze literally millions of unstructured documents that can be merged into a single SOM. The SOM deals not only with individual unstructured documents but relationships between documents as well. The SOM may show text that is correlated to other text. For example, in the medical field, working with medical patient records, this ability to correlate is very attractive. The SOM also allows the analyst to see the larger picture as well as drilling down to the detailed picture. The SOM goes down to the individual stemmed-text level, and that is as accurate as textual processing can become. All these characteristics have resulted in the growing popularity of SOM visualizations in order to assist visual inspection of complex high-dimensional data. For the end user the flexibility of the SOM algorithm is defined through a number of parameters. For appropriate configuration of the network, and tuning the visualization output, user-defined parameters include grid dimensions (2-D, 3-D), grid shape (rectangle, hexagon), number of output nodes, neighborhood function, heighborhood size, learning-rate function, initial weights in the network, way of learning and number of iterations, and order of input samples.
15.6 VISUALIZATION SYSTEMS FOR DATA MINING
Many organizations, particularly within the business community, have made significant investments in collecting, storing, and converting business information into results that can be used. Unfortunately, typical implementations of business “intelligence software” have proven to be too complex for most users except for their core reporting and charting capabilities. Users’ demands for multidimensional analysis, finer data granularity, and multiple-data sources, simultaneously, all at Internet speed, require too much specialist intervention for broad utilization. The result is a report explosion in which literally hundreds of predefined reports are generated and pushed throughout the organization. Every report produces another. Presentations get more complex. Data are exploding. The best opportunities and the most important decisions are often the hardest to see. This is in direct conflict with the needs of frontline decision makers and knowledge workers who are demanding to be included in the analytical process.