Data Mining (88 page)
Authors: Mehmed Kantardzic
11.3 HITS AND LOGSOM ALGORITHMS
To date, index-based search engines for the Web have been the primary tool with which users search for information. Experienced Web surfers can make effective use of such engines for tasks that can be solved by searching with tightly constrained keywords and phrases. These search engines are, however, unsuited for a wide range of less precise tasks. How does one select a subset of documents with the most value from the millions that a search engine has prepared for us? To distill a large Web-search topic to a size that makes sense to a human user, we need a means of identifying the topic’s most authoritative Web pages. The notion of authority adds a crucial dimension to the concept of relevance: We wish to locate not only a set of relevant pages, but also those that are of the highest quality.
It is important that the Web consists not only of pages, but also hyperlinks that connect one page to another. This hyperlink structure contains an enormous amount of information that can help to automatically infer notions of authority. Specifically, the creation of a hyperlink by the author of a Web page represents an implicit endorsement of the page being pointed to. By mining the collective judgment contained in the set of such endorsements, we can gain a richer understanding of the relevance and quality of the Web’s contents. It is necessary for this process to uncover two important types of pages:
authorities
, which provide the best source of information about a given topic and
hubs
, which provide a collection of links to authorities.
Hub pages appear in a variety of forms, ranging from professionally assembled resource lists on commercial sites to lists of recommended links on individual home pages. These pages need not themselves be prominent, and working with hyperlink information in hubs can cause much difficulty. Although many links represent some kind of endorsement, some of the links are created for reasons that have nothing to do with conferring authority. Typical examples are navigation and paid advertisement hyperlinks. A hub’s distinguishing feature is that they are potent conferrers of authority on a focused topic. We can define a
good hub
if it is a page that points to many good authorities. At the same time, a good authority page is a page pointed to by many good hubs. This mutually reinforcing relationship between hubs and authorities serves as the central idea applied in the
HITS algorithm
that searches for good hubs and authorities. The two main steps of the HITS algorithm are
1.
the sampling component
, which constructs a focused collection of Web pages likely to be rich in relevant information, and
2.
the weight-propagation component
, which determines the estimates of hubs and authorities by an iterative procedure and obtains the subset of the most relevant and authoritative Web pages.
In the sampling phase, we view the Web as a directed graph of pages. The HITS algorithm starts by constructing the subgraph in which we will search for hubs and authorities. Our goal is a subgraph rich in relevant, authoritative pages. To construct such a subgraph, we first use query terms to collect a root set of pages from an index-based search engine. Since many of these pages are relevant to the search topic, we expect that at least some of them are authorities or that they have links to most of the prominent authorities. We therefore expand the root set into a base set by including all the pages that the root-set pages link to, up to a designated cutoff size. This base set V typically contains from 1000 to 5000 pages with corresponding links, and it is a final result of the first phase of HITS.
In the weight-propagation phase, we extract good hubs and authorities from the base set V by giving a concrete numeric interpretation to all of them. We associate a nonnegative authority weight
a
p
and a nonnegative hub weight
h
p
with each page p ∈ V. We are interested only in the relative values of these weights; therefore, normalization is applied so that their total sum remains bounded. Since we do not impose any prior estimates, we set all
a
and
h
values to a uniform constant initially. The final weights are unaffected by this initialization.
We now update the authority and hub weights as follows. If a page is pointed to by many good hubs, we would like to increase its authority weight. Thus, we update the value of a
p
for the page p to be the sum of h
q
over all pages q that link to p:
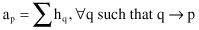
where the notation q→p indicates that page q links to page p. In a strictly dual fashion, if a page points to many good authorities, we increase its hub weight
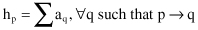
There is a more compact way to write these updates. Let us number the pages {1,2, … , n}, and define their adjacency matrix A to be n × n matrix whose (i, j)
th
element is equal to 1 if page i links to page j, and 0 otherwise. All pages at the beginning of the computation are both hubs and authorities, and, therefore, we can represent them as vectors

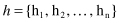
Our update rules for authorities and hubs can be written as
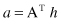
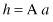
or, substituting one into another relation,
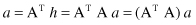
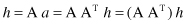
These are relations for iterative computation of vectors
a
and
h
. Linear algebra tells us that this sequence of iterations, when normalized, converges to the principal eigenvector of A
T
A. This says that the hub and authority weights we compute are truly an intrinsic feature of the linked pages collected, not an artifact of our choice of initial weights. Intuitively, the pages with large weights represent a very dense pattern of linkage, from pages of large hub weights to pages of large authority weights. Finally, HITS produces a short list consisting of the pages with the largest hub weights and the pages with the largest authority weights for the given search topic. Several extensions and improvements of the HITS algorithm are available in the literature. Here we will illustrate the basic steps of the algorithm using a simple example.
Suppose that a search engine has selected six relevant documents based on our query, and we want to select the most important authority and hub in the available set. The selected documents are linked into a directed subgraph, and the structure is given in Figure
11.2
a, while corresponding adjacency matrix A and initial weight vectors
a
and
h
are given in Figure
11.2
b.