Data Mining (86 page)
Authors: Mehmed Kantardzic
In our example in the second iteration, starting with attribute A
2
, MD pattern (*, 2, *
)
will be found
.
Including dimension A
3
, there are no additional MD patterns. The third and last iteration in our example starts with the A
3
dimension and the corresponding pattern is (*, *, m).
In summary, the modified BUC algorithm defines a set of MD patterns with the corresponding projections of a database. The processing tree for our example of database DB is shown in Figure
10.8
. Similar trees will be generated for a larger number of dimensions.
Figure 10.8.
A processing tree using the BUC algorithm for the database in Table
10.4
.
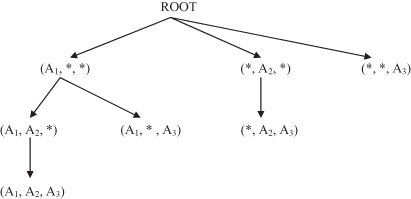
When all MD patterns are found, the next step in the analysis of multidimensional-transactional database is the mining of frequent itemsets in the MD-projected database for each MD pattern. An alternative approach is based on finding frequent itemsets first and then the corresponding MD patterns.
10.8 REVIEW QUESTIONS AND PROBLEMS
1.
What is the essential difference between association rules and decision rules (described in Chapter 6)?
2.
What are the typical industries in which market-basket analysis plays an important role in the strategic decision-making processes?
3.
What are the common values for support and confidence parameters in the
Apriori
algorithm? Explain using the retail industry as an example.
4.
Why is the process of discovering association rules relatively simple compared with generating large itemsets in transactional databases?
5.
Given a simple transactional database X:
| X: | TID | Items |
| | T01 | A, B, C, D |
| | T02 | A, C, D, F |
| | T03 | C, D, E, G, A |
| | T04 | A, D, F, B |
| | T05 | B, C, G |
| | T06 | D, F, G |
| | T07 | A, B, G |
| | T08 | C, D, F, G |
Using the threshold values support = 25% and confidence = 60%,
(a)
find all large itemsets in database X;
(b)
find strong association rules for database X;
(c)
analyze misleading associations for the rule set obtained in (b).
6.
Given a transactional database Y:
| Y: | TID | Items |
| | T01 | A1, B1, C2 |
| | T02 | A2, C1, D1 |
| | T03 | B2, C2, E2 |
| | T04 | B1, C1, E1 |
| | T05 | A3, C3, E2 |
| | T06 | C1, D2, E2 |
Using the threshold values for support s = 30% and confidence c = 60%,
(a)
find all large itemsets in database Y;
(b)
if itemsets are organized in a hierarchy so that A = {A1, A2, A3},
B = {B1, B2}, C = {C1, C2, C3}, D = {D1, D2}, and E = {E1, E2}, find large itemsets that are defined on the conceptual level including a hierarchy of items;
(c)
find strong association rules for large itemsets in (b).
7.
Implement the
Apriori
algorithm and discover large itemsets in transactional database.
8.
Search the Web to find the basic characteristics of publicly available or commercial software tools for association-rule discovery. Document the results of your search.
9.
Given a simple transactional database, find FP tree for this database if
(a)
support threshold is 5;
(b)
support threshold is 3.
| TID | Items |
| 1 | a b c d |
| 2 | a c d f |
| 3 | c d e g a |
| 4 | a d f b |
| 5 | b c g |
| 6 | d f g |
| 7 | a b g |
| 8 | c d f g |
10.
Given a simple transaction database:
| TID | Items |
| 1 | X Z V |
| 2 | X Y U |
| 3 | Y Z V |
| 4 | Z V W |
Using two iterations of the
Apriori
algorithm find large 2-itemsets if required support is s ≥ 50%. Show all steps of the algorithm.
11.
Given a frequent itemset A,B,C,D, and E, how many possible association rules exist?
12.
What are the frequent itemsets with a minimum support of 3 for the given set of transactions?
| TID | Items |
| 101 | A,B,C,D,E |
| 102 | A,C,D |
| 103 | D,E |
| 104 | B,C,E |
| 105 | A,B,D,E |
| 106 | A,B |
| 107 | B,D,E |
| 108 | A,B,D |
| 109 | A,D |
| 110 | D,E |
13.
The
conviction
is a measure for an analysis of a quality of association rules. The formula for conviction CV in terms of probabilities is given as:
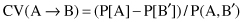
or in terms of support and confidence of an association rule:
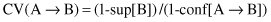
What are basic characteristics of the
conviction
measure? Explain the meaning of some characteristic values.
14.
Consider the dataset given in the table below.
| Customer ID | Transaction Id | Items |
| 418 | 234145 | {X, Z} |
| 345 | 543789 | {U, V, W, X, Y, Z} |
| 323 | 965157 | {U, W, Y} |
| 418 | 489651 | {V, X, Z} |
| 567 | 748965 | {U, Y} |
| 567 | 325687 | {W, X, Y} |
| 323 | 147895 | {X, Y, Z} |
| 635 | 617851 | {U, Z} |
| 345 | 824697 | {V, Y} |
| 635 | 102458 | {V, W, X} |
(a)
Compute the support for item sets {Y}, {X, Z} and {X, Y, Z} by treating each transaction ID as a market basket.
(b)
Use the results from part (a) to compute the confidence for rules XZ → Y and Y → XZ.
(c)
Repeat part (a) by treating each customer ID as a market basket. Each item should be treated as a binary variable (1 if an item appears in at least one transaction bought by the customer, and 0 otherwise).
(d)
Use the results from part (c) to compute the confidence for rules XZ → Y and Y → XZ.
(e)
Find FP-tree for this database if support threshold is 5.
15.
A collection of market-basket data has 100,000 frequent items, and 1,000,000 infrequent items. Each pair of frequent items appears 100 times; each pair consisting of one frequent and one infrequent item appears 10 times, and each pair of infrequent items appears once. Answer each of the following questions. Your answers only have to be correct to within 1%, and for convenience, you may optionally use scientific notation, for example, 3.14 × 10
8
instead of 314,000,000.
(a)
What is the total number of pair occurrences? That is, what is the sum of the counts of all pairs?
(b)
We did not state the support threshold, but the given information lets us put bounds on the support threshold s. What are the tightest upper and lower bounds on s?
10.9 REFERENCES FOR FURTHER STUDY
Adamo, J.,
Data Mining for Association Rules and Sequential Patterns
, Springer, Berlin, 2001.
This book presents a collection of algorithms for data mining on the lattice structure of the feature space. Given the computational complexity and time requirements of mining association rules and sequential patterns, the design of efficient algorithms is critical. Most algorithms provided in the book are designed for both sequential and parallel execution, and they support sophisticated data mining of large-scale transactional databases.
Cheng J., Y. Ke, W. Ng, A Survey on Algorithms for Mining Frequent Itemsets Over Data Streams,
Knowledge and Information Systems
, Vol. 16, No. 1, 2008, pp.1–27.
The increasing prominence of data streams arising in a wide range of advanced applications such as fraud detection and trend learning has led to the study of online mining of frequent itemsets. Unlike mining static databases, mining data streams poses many new challenges. In addition to the one-scan nature, the unbounded memory requirement and the high data arrival rate of data streams, the combinatorial explosion of itemsets exacerbates the mining task. The high complexity of the frequent itemset mining problem hinders the application of the stream-mining techniques. We recognize that a critical review of existing techniques is needed in order to design and develop efficient mining algorithms and data structures that are able to match the processing rate of the mining with the high arrival rate of data streams. Within a unifying set of notations and terminologies, we describe in this paper the efforts and main techniques for mining data streams and present a comprehensive survey of a number of the state-of-the-art algorithms on mining frequent itemsets over data streams.
Goethals B., Frequent Set Mining, in
Data Mining and Knowledge Discovery Handbook
, Maimon L., Rokach L., ed., Springer, New York, 2005, pp. 377–397.
Frequent sets lie at the basis of many data-mining algorithms. As a result, hundreds of algorithms have been proposed in order to solve the frequent set mining problem. In this chapter, we attempt to survey the most successful algorithms and techniques that try to solve this problem efficiently. During the first 10 years after the proposal of the frequent set mining problem, several hundreds of scientific papers were written on the topic and it seems that this trend is keeping its pace.
Han, J., M. Kamber,
Data Mining: Concepts and Techniques
, 2nd edition, Morgan Kaufmann, San Francisco, 2006.