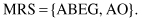Data Mining (90 page)
Authors: Mehmed Kantardzic
The SOM organizes Web pages into similar classes based on users’ navigation patterns. The blank nodes in the table show that there are no corresponding URLs, while the numbered nodes indicate the number of URLs contained within each node (or within each class). The distance on the map indicates the similarity of the Web pages measured by the user-navigation patterns. For example, the number 54 in the last row shows that 54 Web pages are grouped in the same class because they have been accessed by similar types of people, as indicated by their transaction patterns. Similarity here is measured not by similarity of content but by similarity of usage. Therefore, the organization of the Web documents in this graphical representation is based solely on the users’ navigation behavior.
What are the possible applications of the LOGSOM methodology? The ability to identify which Web pages are being accessed by a company’s potential customers gives the company information to make improved decisions. If one Web page within a node successfully refers clients to the desired information or desired page, the other pages in the same node are likely to be successful as well. Instead of subjectively deciding where to place an Internet advertisement, the company can now decide objectively, supported directly by the user-navigation patterns.
11.4 MINING PATH–TRAVERSAL PATTERNS
Before improving a company’s Web site, we need a way of evaluating its current usage. Ideally, we would like to evaluate a site based on the data automatically recorded on it. Each site is electronically administered by a Web server, which logs all activities that take place in it in a file called a Web-server log. All traces left by the Web users are stored in this log. Therefore, from these log files we can extract information that indirectly reflects the site’s quality by applying data-mining techniques. We can mine data to optimize the performance of a Web server, to discover which products are being purchased together, or to identify whether the site is being used as expected. The concrete specification of the problem guides us through different data-mining techniques applied to the same Web-server log.
While the LOGSOM methodology is concentrated on similarity of Web pages, other techniques emphasize the similarity of a user’s paths through the Web. Capturing user-access patterns in a Web environment is referred to as
mining path–traversal patterns
. It represents an additional class of data-mining techniques, which is showing great promise. Note that because users travel along information paths to search for the desired information, some objects or documents are visited because of their location rather than their content. This feature of the traversal pattern unavoidably increases the difficulty of extracting meaningful information from a sequence of traversal data, and explains the reason why current Web-usage analyses are mainly able to provide statistical information for traveling points, but not for traveling paths. However, as these information-providing services become increasingly popular, there is a growing demand for capturing user-traveling behavior to improve the quality of such services.
We first focus on the theory behind the navigational patterns of users in the Web. It is necessary to formalize known facts about navigation: that not all pages across a path are of equal importance, and that users tend to revisit pages previously accessed. To achieve a data-mining task, we define a navigation pattern in the Web as a generalized notion of a sequence, the materialization of which is the directed-acyclic graph. A sequence is an ordered list of items, in our case Web pages, ordered by time of access. The log file L is a multiset of recorded sequences. It is not a simple set, because a sequence may appear more than once.
When we want to observe sequence
s
as a concatenation of the consecutive subsequences
x
and
y
, we use the notation:
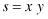
The function
length
(
s
) returns the number of elements in the sequence
s
. The function
prefix
(
s
, i) returns the subsequence composed of the first i elements of
s
. If
s
’ =
prefix
(
s
,i), we say that
s
’ is a prefix of
s
and is denoted as
s
’ ≤
s
. Analysis of log files shows that Web users tend to move backwards and revisit pages with a high frequency. Therefore, a log file may contain duplicates. Such revisits may be part of a guided tour or may indicate disorientation. In the first case, their existence is precious as information and should be retained. To model cycles in a sequence, we label each element of the sequence with its occurrence number within the sequence, thus distinguishing between the first, second, third, and so on occurrence of the same page.
Moreover, some sequences may have common prefixes. If we merge all common prefixes together, we transform parts of the log file into a tree structure, each node of which is annotated with the number of sequences having the same prefix up to and including this node. The tree contains the same information as the initial log file. Hence, when we look for frequent sequences, we can scan the tree instead of the original log multiset. On the tree, a prefix shared among
k
sequences appears and gets tested only once.
Sequence mining can be explained as follows: Given a collection of sequences ordered in time, where each sequence contains a set of Web pages, the goal is to discover sequences of maximal length that appear more frequently than a given percentage threshold over the whole collection. A frequent sequence is maximal if all sequences containing it have a lower frequency. This definition of the sequence-mining problem implies that the items constituting a frequent sequence need not necessarily occur adjacent to each other. They just appear in the same order. This property is desirable when we study the behavior of Web users because we want to record their intents, not their errors and disorientations.
Many of these sequences, even those with the highest frequencies, could be of a trivial nature. In general, only the designer of the site can say what is trivial and what is not. The designer has to read all patterns discovered by the mining process and discard unimportant ones. It would be much more efficient to automatically test data-mining results against the expectations of the designer. However, we can hardly expect a site designer to write down all combinations of Web pages that are considered typical; expectations are formed in the human mind in much more abstract terms. Extraction of informative and useful maximal sequences continues to be a challenge for researchers.
Although there are several techniques proposed in the literature, we will explain one of the proposed solutions for mining traversal patterns that consists of two steps:
(a)
In a first step, an algorithm is developed to convert the original sequence of log data into a set of
traversal subsequences
. Each traversal subsequence represents a maximum forward reference from the starting point of a user access. It should be noted that this step of conversion would filter out the effect of backward references, which are mainly made for ease of traveling. The new reduced set of user-defined forward paths enables us to concentrate on mining meaningful user-access sequences.
(b)
The second step consists of a separate algorithm for determining the frequent-traversal patterns, termed
large reference sequences
. A large reference sequence is a sequence that appears a sufficient number of times in the log database. In the final phase, the algorithm forms the
maximal references
obtained from large reference sequences. A maximal large sequence is a large reference sequence that is not contained in any other maximal reference sequence.
For example, suppose the traversal log of a given user contains the following path (to keep it simple, Web pages are represented by letters):
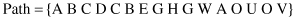
The path is transformed into the tree structure shown in Figure
11.3
. The set of maximum forward references (MFR) found in step (a) after elimination of backward references is
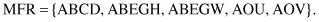
Figure 11.3.
An example of traversal patterns.
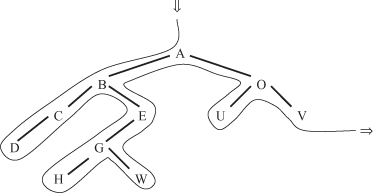
When MFR have been obtained for all users, the problem of finding frequent-traversal patterns is mapped into one of finding frequently occurring consecutive subsequences among all MFR. In our example, if the threshold value is 0.4 (or 40%), large-reference sequences (LRS) with lengths 2, 3, and 4 are
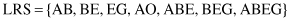
Finally, with LRS determined,
maximal reference sequences
(MRS) can be obtained through the process of selection. The resulting set for our example is