The Norm Chronicles (22 page)

The German poet Friedrich von Schiller said similarly: ‘There is no such thing as chance; and what seem to us merest accident springs from the deepest source of destiny.’ All things happen for a reason.

A similar reaction to chance is superstition, by which people hope that rituals and totems will turn fate to their advantage, perhaps by finding favour with the Gods, perhaps through mystical connection with natural power, and where today’s lucky sporting mascots are the sanitised versions of Aztec human sacrifice. Fate calls the shots, but likes a bribe. The piano misses because Kevin must have slaughtered a sheep at high tide at midnight.

Even 2,000 years ago there were ‘rationalists’ who scorned these beliefs. Oddly, Professor Kevin would have liked their style. In Roman times, three 6s from three dice was known as ‘the Venus throw’. Cicero said: ‘Are we going to be so feeble-minded then as to aver that such a thing happened by the personal intervention of Venus rather than by pure luck?’ He taunted astrologers with relish.

Cicero, like Kevin, defends freedom from necessity. In Cicero we see this as rationality at war with superstition. Kevin sees it as anti-rationality in favour of chaos and impulse.

As the scientific enlightenment developed in the late 17th century, earthly causes challenged mystical ones, and the extraordinary explanatory power of Newton’s laws of motion led to the belief, in the physical world at least, that all matter moved like clockwork: if we knew precisely the position and motion of every atom, then in principle we could predict exactly what would happen. Thus again, the piano misses Kevin because the precise chain of causality between atoms, forces and initial conditions following given laws, plots its course, just shy of his nose. And again, there is nothing inherently random about it. Any uncertainty in this world is ‘a measure of our ignorance’ – as the statistician Pierre Laplace said – ignorance not of God’s will this time but of the state and laws of nature; not so much ‘can’t know’ as ‘don’t know’.

Two words summarise these two types of uncertainty. The first is ‘aleatory’, used to describe the uncertainty before a coin is flipped when we simply cannot know what will happen, often known as chance or randomness. The second is ‘epistemic’, used for the uncertainty when we have
flipped the coin but not looked at it, in which case we don’t know but in theory could – more commonly called lack of knowledge or ignorance. Although there are inevitable complications: what if it’s a two-headed coin? Then what you thought was chance was tainted by ignorance.

The ‘don’t know’ that applied to human knowledge of the mind of God and the ‘don’t know’ that described our limited understanding of nature’s clockwork implied that with more knowledge we would uncover the rigid determinism that explained human behaviour fully. Either way, everything had a cause that began outside ourselves.

This spooked people. For both kinds of ignorance – of divine cause and physical cause – seemed contrary to our internal sense of free will, and neither our own life nor other people’s behaviour appears to us to obey the mechanics of a pendulum. So at this stage (and ever since), there were fierce arguments in both religion and science about whether people’s sense of their own freedom of choice was an illusion.

Then came the grand age of statistics, when people were initially drawn further into the net of predictability. From the early 19th century there was an obsessive listing of deaths, crimes and, particularly, suicides. And what emerged was an extraordinary regularity, even from the turmoil of individual decisions, an order that seemed to emerge as if by a natural law and so raise doubts about the scope for chance. Because despite the choices of millions, each in unique circumstances, there seemed to be some regularising force that led to an almost constant number of suicides each year. Other patterns also emerged from the data. Francis Galton, a cousin of Charles Darwin, said famously: ‘Whenever a large sample of chaotic elements are taken in hand and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along.’ Some came to the conclusion that these predictable patterns meant that chance could not exist.

But although there was order in human behaviour en masse, there was still mystery about how this order would shape any individual. Yes, there would be a roughly predictable number of suicides, but still it was not possible to say by whom. The average, the trend and the distribution were indeed observable, but the particular was not predictable.

This led to the idea that we are all random deviations from Quetelet’s average man or
‘homme moyen
’ (described in
Chapter 13
). Kevin is more than happy to be such a deviation.

There were strikingly similar developments in the physical sciences. Quetelet described his work as ‘social physics’, and his ideas, published between the 1820s and 1860s, may have influenced James Clerk Maxwell’s development of Bernoulli’s kinetic theory of gases, which describes the overall behaviour of a gas as akin to a vast blizzard of colliding individual particles. This parallel between social and physical science doesn’t receive the attention it deserves, but it is a remarkable intellectual co-evolution that seems to offer a way of comparing human experience with the behaviour of matter. Here too, although it was impossible to predict the motion of each of the zillions of molecules bouncing around in a gas, even if this motion was in theory fully determined, probability could successfully explain the overall movement, just as it can describe overall patterns in people’s behaviour. In fact, there is an argument that without probability we would be unable to appreciate large-scale change in people or in physics.
*
We would sit there watching a zillion random events among humans and molecules, with little sense of a bigger picture.

In theory, again, it was
possible
for all the molecules to wander off suddenly in one direction, as when the Improbability Drive in
The Hitchhiker’s Guide to the Galaxy
was ‘originally devised by physicists to transpose the underwear of a hostess at a party several feet away from her body’.
⁴
In practice the behaviour of the whole gas was predictable even
if the behaviour of the parts were in practice not. So in both the social world of people and in the physical world, the aim of predicting what would happen to each little piece, whether a human or molecule, was given up, but a new order was found in the predictability of averages.

Perhaps the best image of the behaviour of molecules is provided each Saturday evening, when 49 balls are banging around in a Perspex bucket, watched by millions of people clutching their National Lottery ticket and hoping their lives will be changed. Six balls are chosen for the jackpot – as we have seen in
Chapter 12
, it makes no difference which set you choose – 1, 2, 3, 4, 5, 6 or any other combination – the chance is still around 1 in 14 million that your choice will come up. Web sites keep track of how often specific numbers come up, with 38 having topped the league table of number of appearances for ages. Surely the law of averages says that 38 is due for a rest and we should keep away from it?

But this isn’t how the law of averages works. What it means is that over time, even though each draw is completely unpredictable and not influenced by what has happened before, the spread of the numbers of appearances of the balls has a regular pattern, as shown in
Figure 17
. All these unpredictable events, when put together, turn out to have their own structure and even their own shape – the beautiful normal curve observed by Quetelet when he measured people’s heights.

So although 38 has popped up 241 times – nearly half as many times again as poor old number 20’s pathetic 171 appearances – this is exactly what could have been predicted back in 1994 using probability theory alone. Of course, we could not have predicted which numbers would be top and bottom, just that one number would have about 240 and one around 170 appearances.

Another wonderful illustration of the patterns of chance comes from a contender for the most boring book in the world –
A Million Random Digits.
⁵
The title says it all – page after page of numbers, with no detectable order, each one utterly unrelated to those that come before. It begins with ‘1’ and finishes with ‘8’, an ending as unpredictable as a good Agatha Christie whodunnit. The audio version would do wonders for insomniacs. And we’re still waiting for the German translation.

Figure 17:
Number of appearances of balls 1 to 49 in 1,740 UK National Lottery draws, November 1994–August 2012

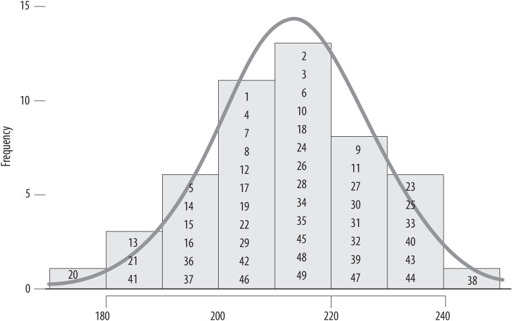
The normal curve is the predicted distribution based on probability theory.

But there are gems hidden in all this randomness. We can expect the sequence 1, 2, 3, 4, 5 to occur ten times (and in fact it occurs eleven times). And we would expect events that have a 1-in-a-million chance, such as the same digit occurring seven times in a row – to turn up once. And, satisfyingly, there is exactly one example of this – 6, 6, 6, 6, 6, 6, 6. And we can even calculate the probability that there would be no such sequence, which turns out to be 37 per cent, so we could have been unlucky.

Probability theory provides a practical way of dealing with the randomness in life – but even the patterns of pure unpredictability don’t really tackle the fundamental question of whether true, absolute, irreducible chance really exists, or whether everything is at some level determined. If we knew everything about those bouncing lottery balls, could we predict which one would drop out? Sadly not, for two main reasons.

First, quantum mechanics came along in the 20th century and said that chance did indeed exist, at least at a sub-atomic level. Essential
parts of the sub-atomic world could only be described as a probability. Heisenberg’s Uncertainty Principle says we can’t know everything about a sub-atomic particle – in terms of both where it is and where it is going. Newton’s laws of causation were inadequate.

Second (and in practice more important than the quantum uncertainty), there is also an effect that throws all expectations into the air. This is chaos theory, in which even if a system were completely deterministic, in the sense that there was no randomness at any point in the chain of causation, some systems – such as the weather – might nevertheless be so dependent on, and so affected by, the tiniest difference in where they start, a difference undetectable by people, that we have no idea how they will turn out.

The standard image is of a butterfly flapping its wings and thus causing some faraway storm. A real example is Clint Dawson’s experience of forest fires. He is an FBAN, a fire behaviour analyst, and his job is to try to predict the course of forest fires in Colorado. In 2012 the fires began to behave with dangerous unpredictability, often burning bigger than before. His computer models of what a fire would do became less accurate. The reason? A series of tiny changes in initial conditions, among them that no one had thought – why would they? – to factor in a change in the behaviour of beetles, of all things. A winter influx of pine beetles had desiccated the trees, making them more flammable.
⁶

The
chaos
idea means that clockwork-like systems can be unpredictable simply because we can never even know exactly where they start, let alone exactly what they will do next. Causation is too complicated. Such systems might as well be ruled by chance after all (whatever that is). Had a butterfly landed on the piano just before the lads moved it, and distracted one of them, it might have made only the tiniest difference, which to Kevin would have been a difference of life and death.

Do these physical limitations on what we can know, chaos and quantum uncertainty, matter on a human scale? Is it odds-on that Kevin’s trust in some fantastical element will be his doom one day? Or are these strange forces only of theoretical importance? How much faith would you have in uncertainty if a piano loomed over your head?

All risk is chance. And chance remains mysterious. Whether it
originates outside people in the deep structures of matter or if it’s all in our heads hardly matters to the uncertainty of living. The practical question is what to do about that: whether to strive for certainty (Prudence), to relish uncertainty (the Kevlin brothers) or to decide that life is about placing your bets (Norm).

15
TRANSPORT

N
ORM SHUFFLED ALONG
the carriage until he found the ideal space, four empty seats, one at the window to watch the station do its strange retreat; him, his thoughts, a book on the table. He liked trains – a good bet for low MicroMorts.

A short, stout, grinning woman with bleached hair wearing an outsize white T-shirt bumped her way into the seat opposite and stuffed her rucksack under the table between her knees. Norm pulled in his feet. She settled, and he reached for his book.