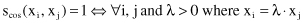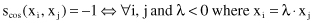Data Mining (72 page)
Authors: Mehmed Kantardzic
A sample can describe either a physical object (a chair) or an abstract object (a style of writing). Samples, represented conventionally as multidimensional vectors, have each dimension as a single feature. These features can be either quantitative or qualitative descriptions of the object. If the individual scalar component x
ij
of a sample x
i
is a feature or attribute value, then each component x
ij
, j = 1, … , m is an element of a domain P
j
, where P
j
could belong to different types of data such as binary (P
j
= {0,1}), integer (P
j
⊆ Z), real number (P
j
⊆ R), or a categorical set of symbols. In the last case, for example, Pj may be a set of colors: P
j
= {white, black, red, blue, green}. If weight and color are two features used to describe samples, then the sample (20, black) is the representation of a black object with 20 units of weight. The first feature is quantitative and the second one is qualitative. In general, both feature types can be further subdivided, and details of this taxonomy are already given in Chapter 1.
Quantitative features can be subdivided as
1.
continuous values
(e.g., real numbers where P
j
⊆ R),
2.
discrete values
(e.g., binary numbers P
j
= {0,1}, or integers P
j
⊆ Z), and
3.
interval values
(e.g., P
j
= {x
ij
≤ 20, 20 < x
ij
< 40, x
ij
≥ 40}.
Qualitative features can be
1.
nominal or unordered
(e.g., color is “blue” or “red”), and
2.
ordinal
(e.g., military rank with values “general” and “colonel”).
Since similarity is fundamental to the definition of a cluster, a measure of the similarity between two patterns drawn from the same feature space is essential to most clustering algorithms. This measure must be chosen very carefully because the quality of a clustering process depends on this decision. It is most common to calculate, instead of the similarity measure, the dissimilarity between two samples using a distance measure defined on the feature space. A distance measure may be a metric or a quasi-metric on the sample space, and it is used to quantify the dissimilarity of samples.
The word “similarity” in clustering means that the value of s(x, x′) is large when x and x′ are two similar samples; the value of s(x, x′) is small when x and x′ are not similar. Moreover, a similarity measure
s
is symmetric:
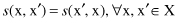
For most clustering techniques, we say that a similarity measure is normalized:
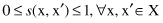
Very often a measure of dissimilarity is used instead of a similarity measure. A dissimilarity measure is denoted by d(x, x′), ∀x, x′ ∈ X. Dissimilarity is frequently called a distance. A distance d(x, x′) is small when x and x′ are similar; if x and x′ are not similar d(x, x′) is large. We assume without loss of generality that
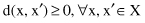
Distance measure is also symmetric:
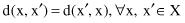
and if it is accepted as a
metric distance measure
, then a triangular inequality is required:
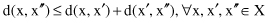
The most well-known metric distance measure is the Euclidean distance in an m-dimensional feature space:
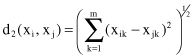
Another metric that is frequently used is called the L
1
metric or city block distance:
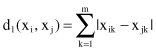
and finally, the Minkowski metric includes the Euclidean distance and the city block distance as special cases:
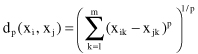
It is obvious that when p = 1, then d coincides with L
1
distance, and when p = 2, d is identical with the Euclidean metric. For example, for 4-D vectors x
1
= {1, 0, 1, 0} and x
2
= {2, 1, −3, −1}, these distance measures are d
1
= 1 + 1 + 4 + 1 = 7, d
2
= (1 + 1 + 16 + 1)
1/2
= 4.36, and d
3
= (1 + 1 + 64 + 1)
1/3
= 4.06.
The Euclidian n-dimensional space model offers not only the Euclidean distance but also other measures of similarity. One of them is called the cosine-correlation:
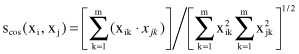
It is easy to see that